はじめに
みなさんこんにちは!
まもなく夏休みも終わりですね。みなさん宿題は終わっていますか?
僕は読書感想文が苦手で最後の1日までやらずに後悔しました。
受験生のみなさんは残り数日の夏休みですが、計画的に進めてくださいね!
さて、今日の問題は「数の性質」についてです。
まずはカンタンな問題から挑戦してみましょう!
「数の性質」のカンタンな問題
 わかみや先生
わかみや先生答えは下にあるので見ないように気をつけてくださいね!
解答
6個
解説を確認しよう!
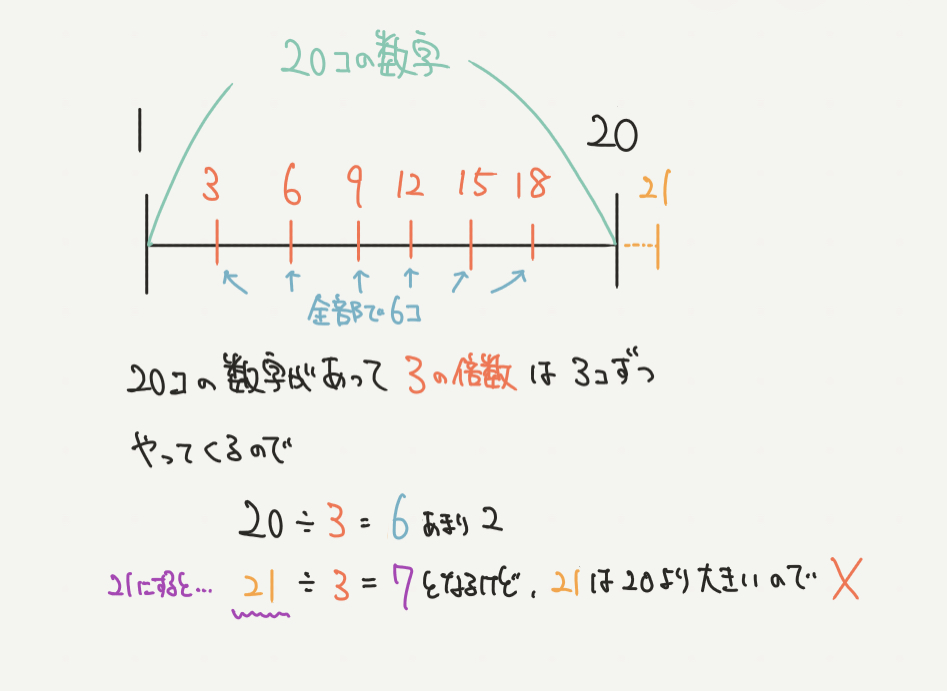

式だけ見ると、
20÷3=6あまり2 となるので、個数は6個とわかります。
この20÷3とはどう言う意味でしょうか?
今回、問題の数字の範囲が1から20までなので数字の個数は20個となりますよね?
そして知りたい3の倍数ですが、
1, 2, [3], 4, 5, [6]‥と3つずつあるので、3で割れば3の倍数が1から20までで6個あるとわかりました。
ちなみにここから何がわかるかというと、
1から20までの数の中で
①3で割れる数は6個
②3で割れない数が20個-6個=14個となります!
さあ、ここまで理解できれば大丈夫!問題に挑戦していきましょう。
問題に挑戦!
解答
答えを見るにはここをクリック!
50個
この記事を書いている人はこんな人


解説を見てみよう!


さて、この問題ではベン図と呼ばれる図が出てきます。
これは数字の数(個数)をもとめるときにとても便利な考え方です。
もし書き方がわからない!という受験生がいたら
下のリンクからベン図の書き方について復習してみるとよりこの問題の解説がわかりやすくなりますよ!




わからなくてもこの解説でもていねいに説明しているので、
ぜひがんばってついてきてくださいね!
STEP1:問題文から正しくベン図を書こう
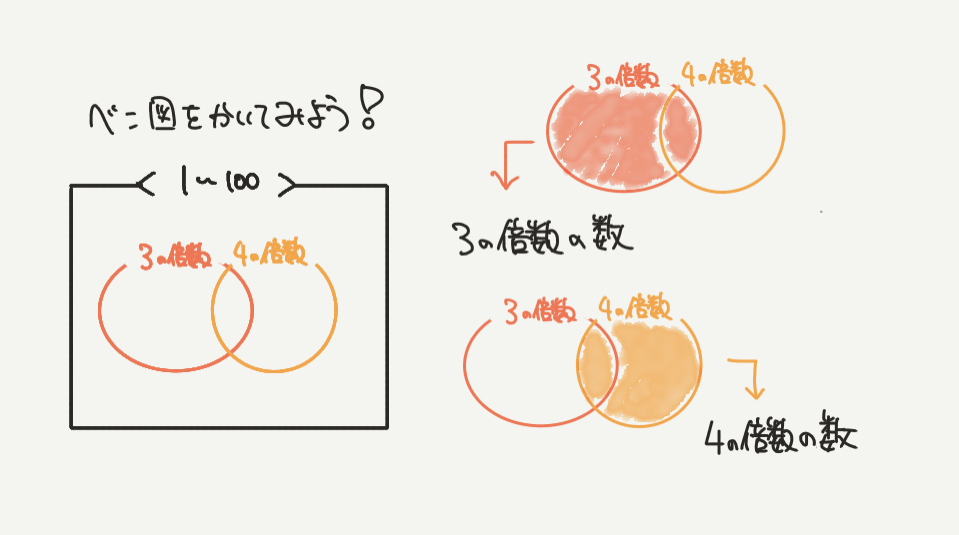

まず最初のSTEP1は問題文をきちんと理解して図にするところから始めましょう。
ベン図はまずはじめに大きな四角形をかき、
その数字の数がどこからどこまでのものなのか(今回は1~100)を書くようにしましょう。
そして100個の数字の中には3の倍数もありますし、4の倍数もありますね。
なのでその数の個数も赤と黄色の円にして書いていきましょう。
少し円を重ねて書くのがポイントです。
なんで重ねないといけないのかは後で説明します!!
STEP2:重なっているところの数に注目する
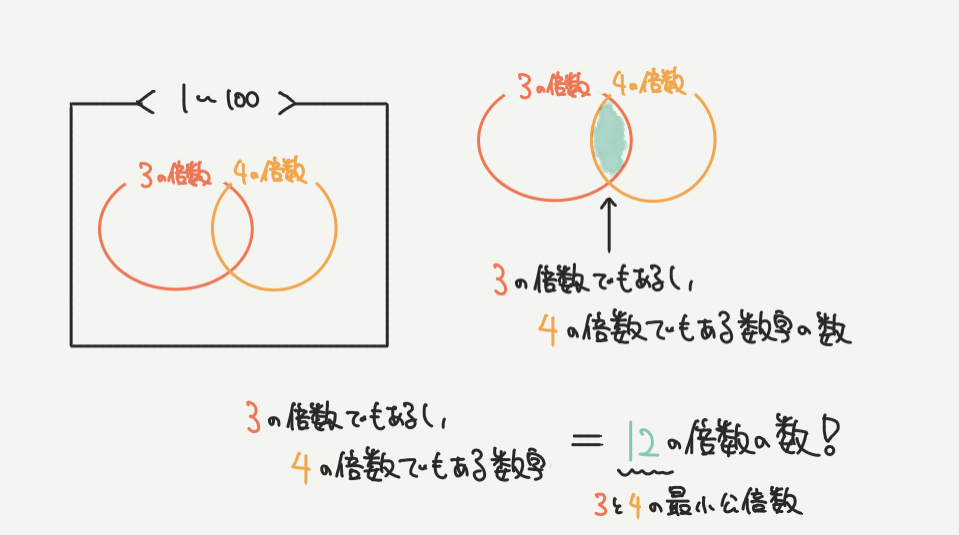

さて、ここで緑の部分が気になると思います。
ここは何かというと、3の倍数でもあるし、4の倍数でもある数の個数です。
例えば12という数は3の倍数でもありますし、4の倍数でもありますよね?
こういう数は3の倍数と4の倍数の性質を持っているので、
円が重なっている部分がこういう12の倍数の数になります。
STEP3:ベン図にわかる数字を書いていこう!
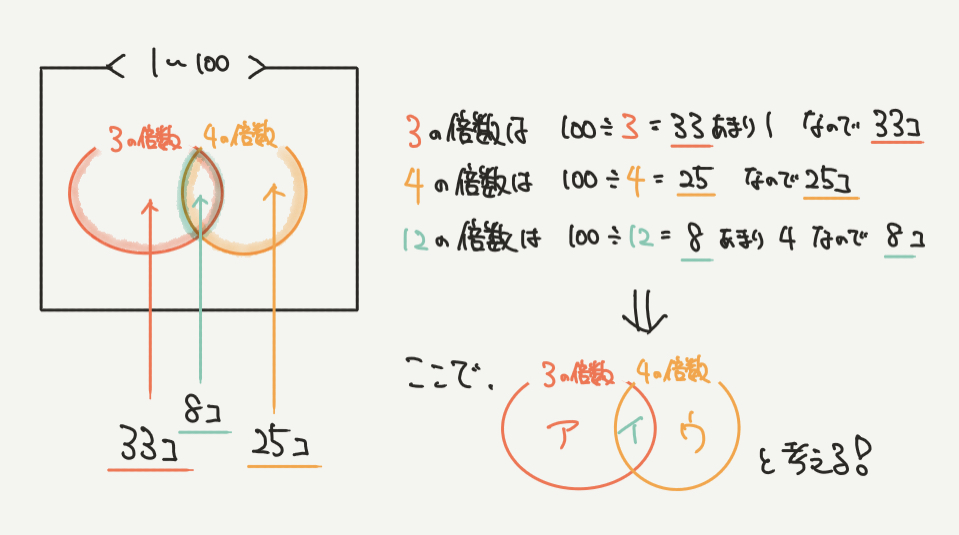

さて、ここまで理解できればあとはわかる数字を書いていきましょう。
例題みたいに数を求めていくと、1から100までの100個の数の中に
3の倍数は33個(100÷3=33あまり1)
4の倍数は25個(100÷4=25)
12の倍数は8個(100÷12=8あまり4)
あることがわかります。
ここで、最後に気をつけて欲しいのがア、イ、ウです!
STEP4:ケアレスミスに注意して答えを求める
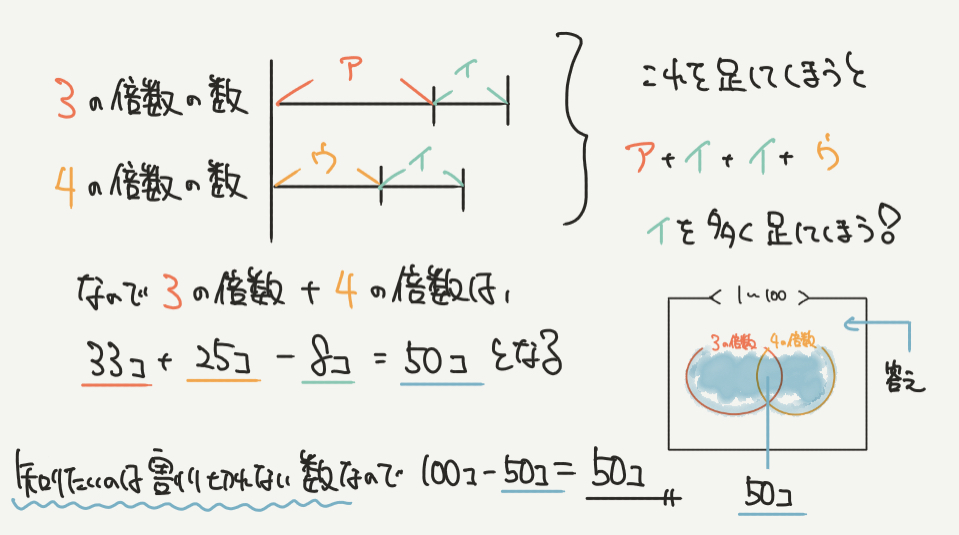

あとは最後に計算するだけです。
3の倍数はア+イ
4の倍数はイ+ウ
ですので、3の倍数と4の倍数の合計の個数は
ア+イ+イ+ウ となります!
でもこれだと、イを2回多く計算してしまいますね。
本当に求めたい数(3の倍数か4の倍数)はア+イ+ウです。
よってア+イ+ウは、
33(3の倍数の数)+25(4の倍数の数)–8(12の倍数)=50個
33(ア+イ)+25(イ+ウ)−8(イ)=50個 になります。
よって青の部分の数が50個とわかりますので、知りたい答え(3の倍数でも4の倍数でもない数)は、
100個−50個=50個 となりました。



今回はたまたま答えが50個と一緒ですが、
まちがえないようにしましょう。
割り切れない数の個数を求める問題のまとめ
今回の問題で大事なポイント
ベン図の書き方(STEP1)
・倍数の個数を図に書いていこう(STEP3)
ベン図の考え方
・重なっているところが12の倍数(STEP2)
こちらでこの問題は終わりです!おつかれさまでした〜〜!!
少しむずかしい問題でしたか?カンタンでしたか?
ベン図の問題で大事なポイントは上の2つです!
きちんとしたベン図を書くこと、数え間違えないように注意すること、
そしてベン図の考え方を理解することが大切でした。
今回は3と4の倍数だけでしたが、受験に出てくるむずかしい問題だと、
倍数の数が3つになったりして、どんどんむずかしくなります。
今のうちにしっかり勉強しておきましょう!