はじめに
みなさんこんにちは!!
今日のテーマは中学受験算数の「平面図形」についてです!
よくあるタイプの円の問題にチャレンジしていきましょう〜。
自信のある受験生はさっそく問題から見てみてください。
まだ解けるかわからないという受験生はヒントの部分から勉強しましょう。
円の問題は楽に計算することが大切
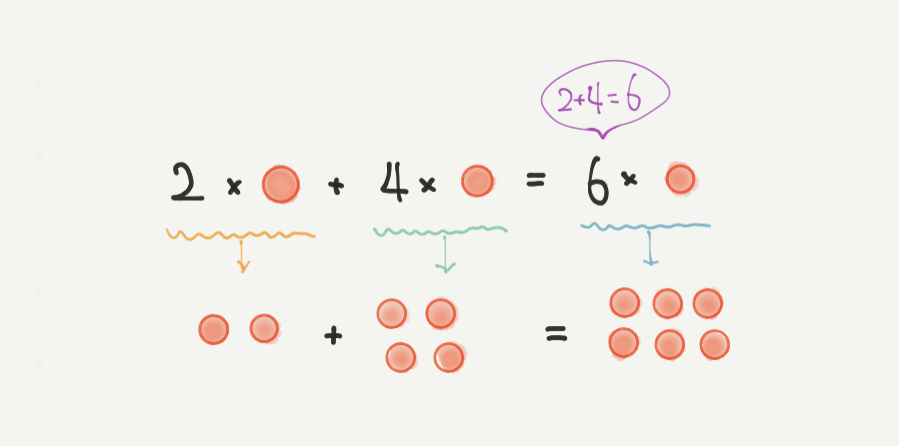
前の記事でも解説しましたが、算数の問題ではいかに早く、正確に解くことができるかが大切になります。
ここで紹介するポイントは、計算スピードを早くし、ミスをできるだけなくすための考え方になります。
まずは上の●を使いながら考えてみましょう。
たとえばこちらの図で、
2×●+4×●という式があったとします。
このときの計算は、(2+4)×●と楽にすることができます。
図にように、2×●を●●とかいて、4×●を●●●●と書いてみると
足し合わさった●の数は6個になるのがわかると思います。
なので、2×●+4×●=6×●と計算を楽にすることができました。
いかがですか?ここまでは理解できましたでしょうか?
前の記事でも解説しましたが、算数の問題ではいかに早く、正確に解くことができるかが大切になります。
ここで紹介するポイントは、計算スピードを早くし、ミスをできるだけなくすための考え方になります。
まずは上の●を使いながら考えてみましょう。
たとえばこちらの図で、
2×●+4×●という式があったとします。
このときの計算は、(2+4)×●と楽にすることができます。
図にように、2×●を●●とかいて、4×●を●●●●と書いてみると
足し合わさった●の数は6個になるのがわかると思います。
なので、2×●+4×●=6×●と計算を楽にすることができました。
いかがですか?ここまでは理解できましたでしょうか?
この前の「円の中の斜線部分の周りの長さと面積を求めるには?」の問題でも出てきたところですね!
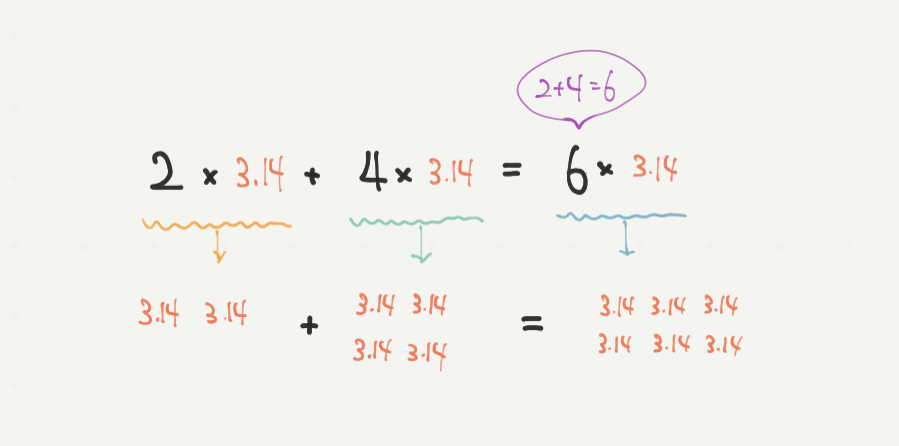
この●を3.14に変えたのが上の図になります。
このときも考え方は全く同じで、2つの式を1つに計算することができます。
●だとわかるのに、●が3.14になると計算できなくなってしまう受験生がたくさんいますので
早めにこの考え方をマスターして使いこなせるようにしておきましょう!
同じ面積の図形を移動させる
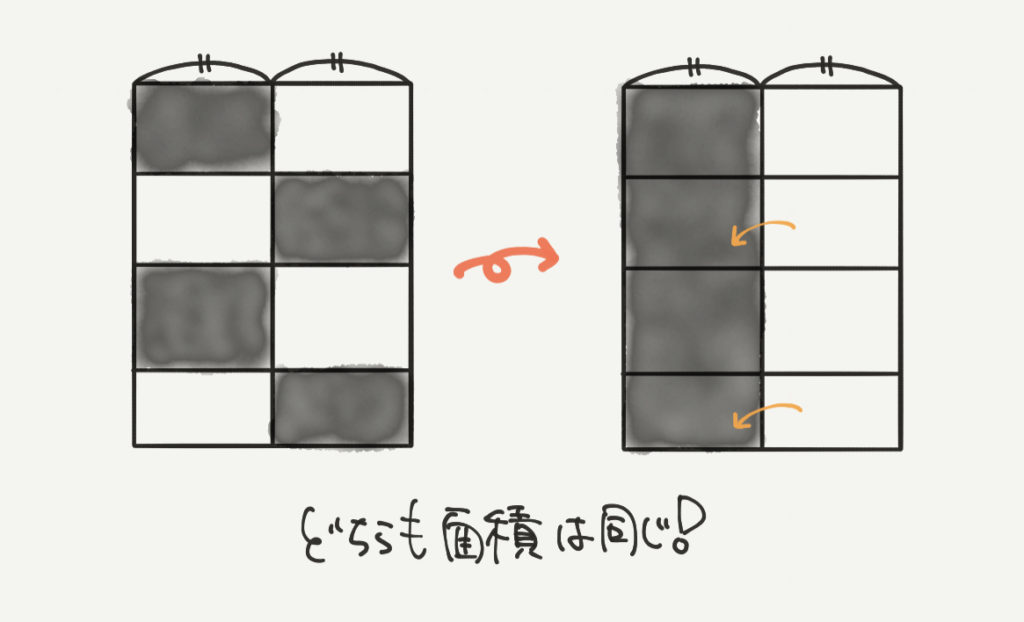
次にポイントとなってくるのが平面図形の移動です。
たとえば、上の図の黒色の面積を少し移動させて右図のようにかんたんにすることができます。
これは「面積が移動させる前と移動させた後で変わらない」からできる考え方になります。
等積変形は同じ面積になるようにある図形を変形させますが、
これはただ面積を移動させているだけなので正確には等積変形とは言えません。
 わかみや先生
わかみや先生今回の問題で必要になってくる考え方はこちらの2つです。
それでは問題にチャレンジしてみましょう!!
問題に挑戦!
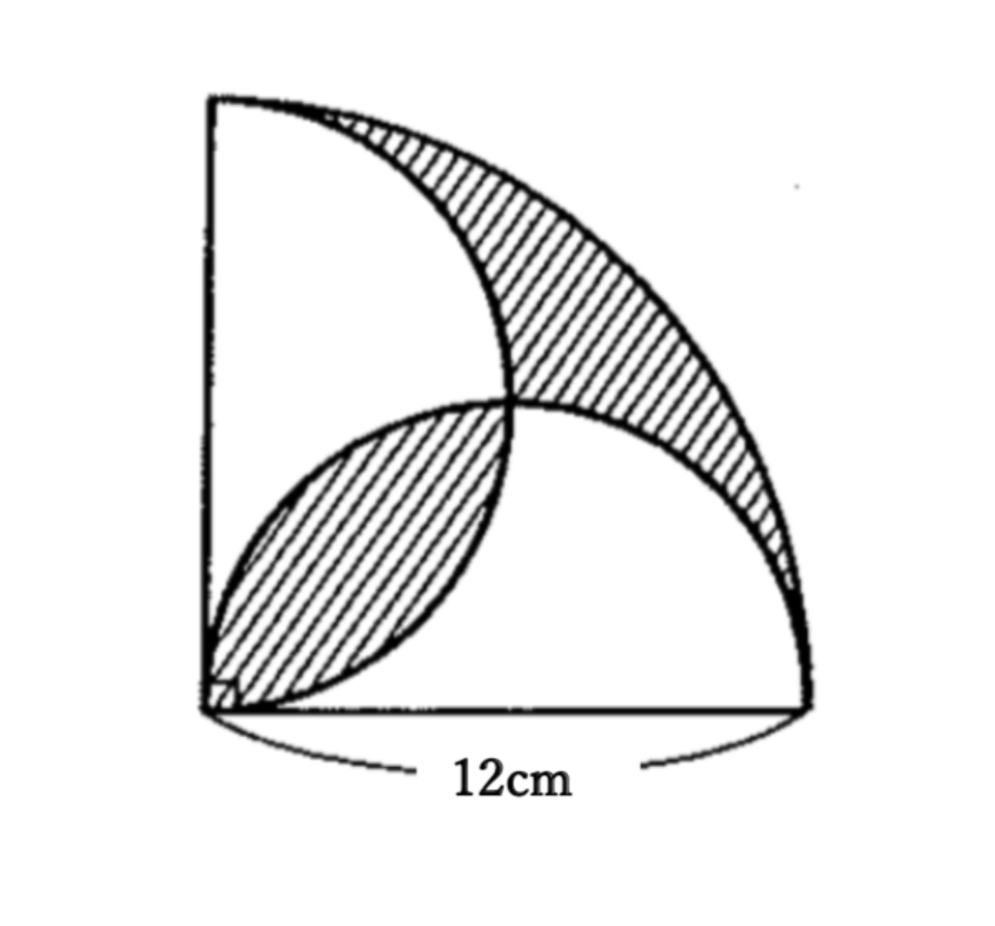

解答
答えを見るにはここをクリック!
①56.52cm
②41.04㎠
この記事を書いている人はこんな人




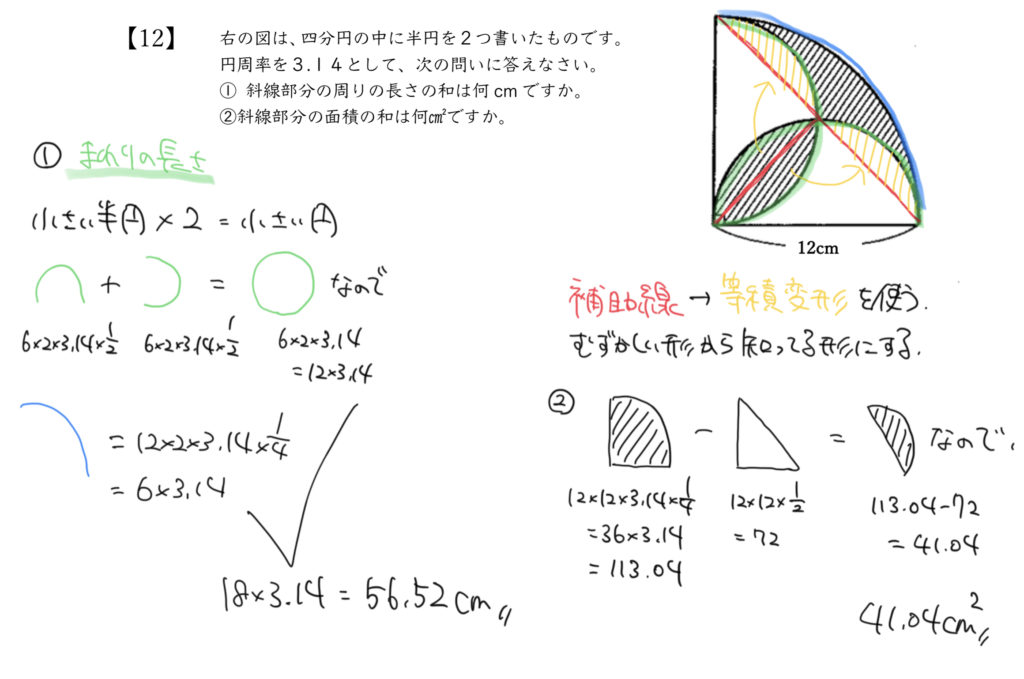
解説を見てみよう!

STEP1:周りの長さは赤+黄+緑
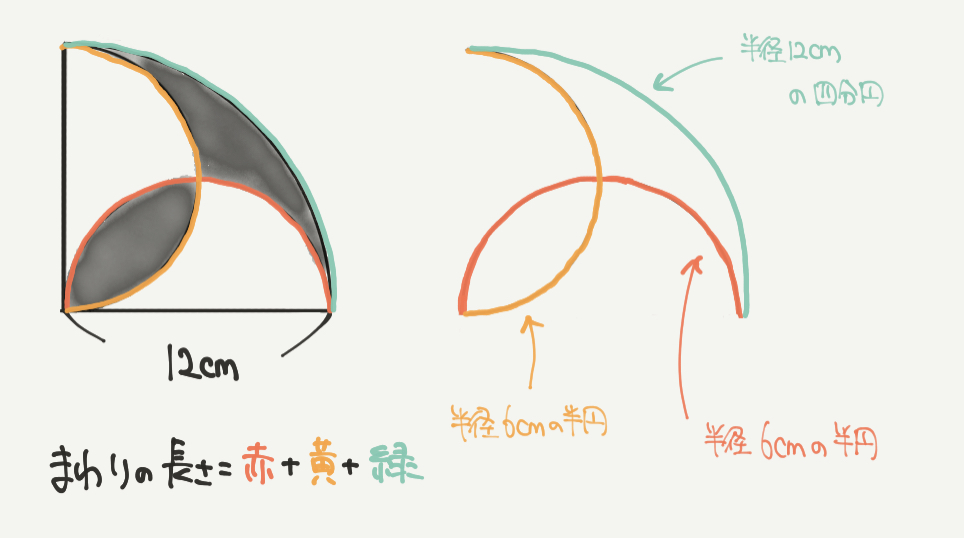

まずは斜線部分の周りの長さから求めていきましょう。
「さんすうがく」では算数に大切な4つの考え方の1つに「全体は部分と部分でできている」という考え方があります。
今回の問題ですと、パッとみてむずかしいような図形の周りの長さも、
赤+黄+緑の3つの部分でできていることがわかります。
なので周りの長さは赤+黄+緑をすれば求めることができますね!
赤:半径6cmの円の半分
黄:半径6cmの円の半分
緑:半径12cmの円の1/4(四分円)
STEP2:周りの長さを楽して計算しよう
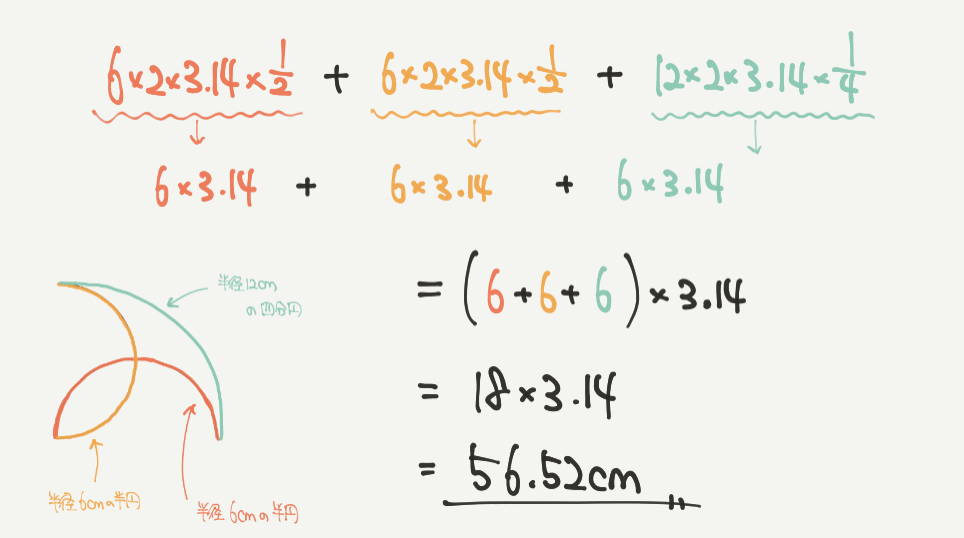
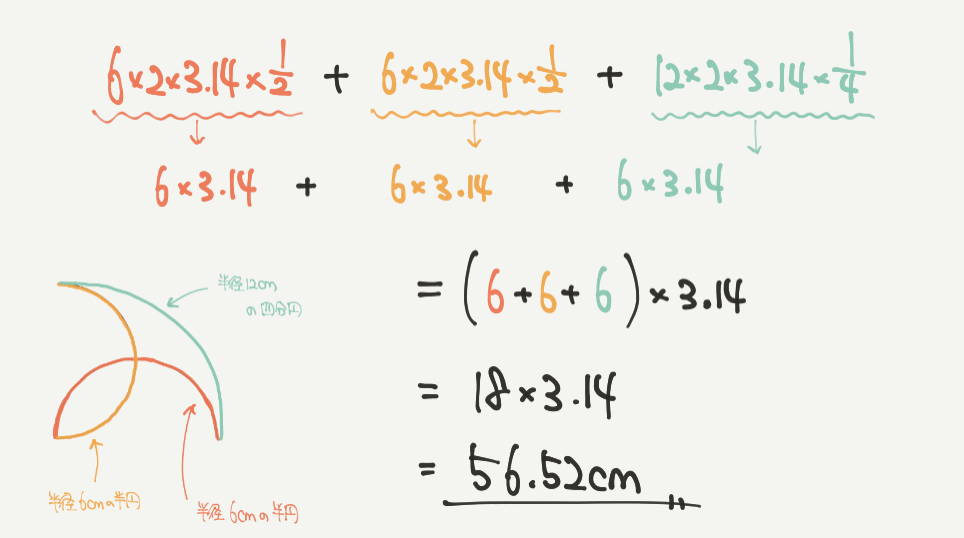
それではSTEP1をふまえて実際に計算してみましょう。
赤:6×2×3.14×1/2
黄:6×2×3.14×1/2
緑:12×2×3.14×1/4



円の面積は「半径×半径×3.14」
円の周りの長さは「半径×2×3.14」になりましたね!
これらを整理すると、
6×3.14+6×3.14+6×3.14
= (6+6+6) ×3.14
=18×3.14
=56.52cm
と求めることができました!
STEP3:図形を移動させてかんたんな形にしよう
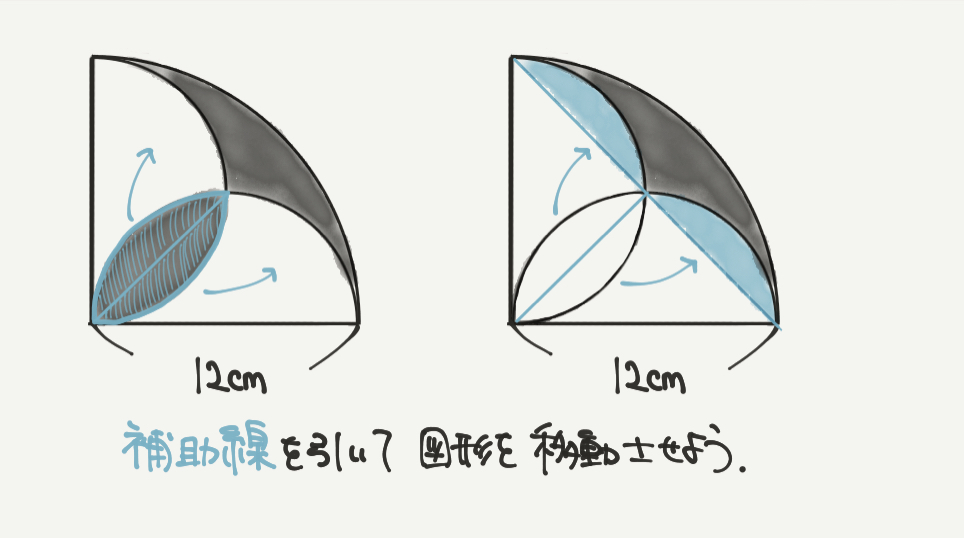

STEP3、4では図形の面積を求めていきましょう。
この図形では青色の補助線を引くことが大切になってきます。
補助線を引いて同じ図形を移動させていきましょう。
補助線は問題を解きやすくするために自分で引く線のことです。
今回は同じ面積の図形を移動させるために補助線を引きました!
STEP4:求めたい図形の面積を求めよう
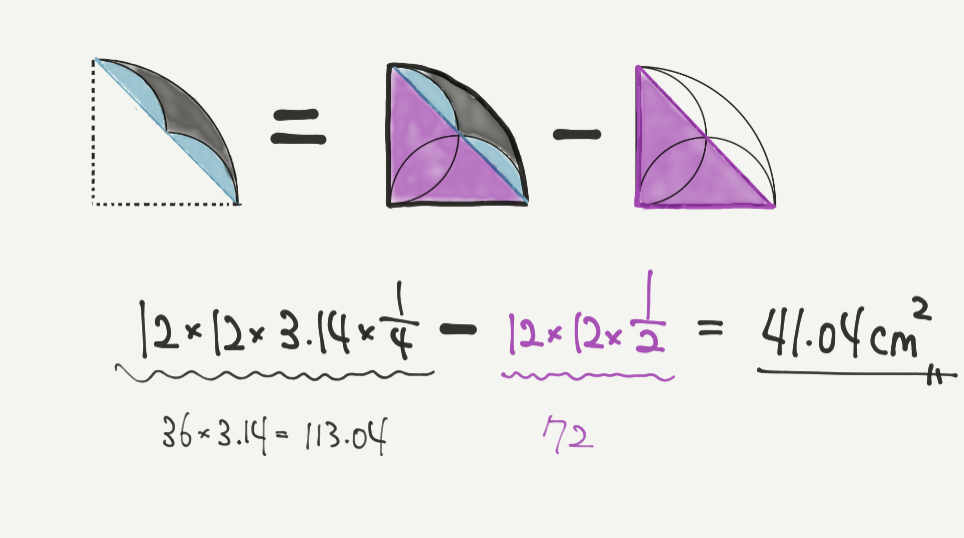
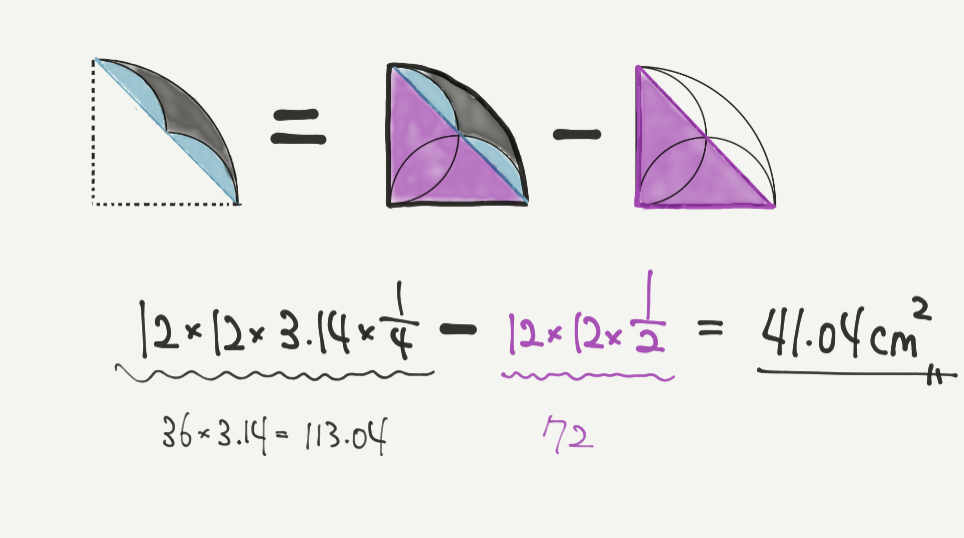
最後に求めたい部分の面積を計算していきましょう。
今回求めたい部分は大きな四分円から紫の三角形を引いた面積になります。
なので、
大きな四分円:12×12×3.14×1/4
三角形:12×12×1/2
よって求めたい答えが
12×12×3.14×1/4-12×12×1/2
=36×3.14-72
=113.04–72
=41.04㎠
と計算することができました。
半円の重なった部分の面積と周りの長さを求める問題の解説
今回の問題で大事なポイント
- 図形を移動させる考え方(はじめに、STEP3)
- 楽に計算するための考え方(はじめに、STEP2、4)
- 「全体は部分と部分でできている」考え方(STEP1)
- 補助線の考え方(STEP3)
今回の問題はこちらで以上です!!
大事なポイントが盛りだくさんの問題でしたね。
特に計算を楽にする考え方と「全体は部分と部分でできている」考え方は
「平面図形」以外の問題にも使われる算数を得意にするためのコツになります。
同じような問題を下に用意しましたので、まだ解いていないよ!という受験生は、
レベルアップのためにぜひ解いてみてください。
円の面積と周りの長さを求める復習
円の中の斜線部分の周りの長さと面積を求めるには?