はじめに
みなさんこんにちは!
今日のテーマは「平面図形」の中でも少し今までと内容が違う問題を解いていきましょう。
今までの「平面図形」の問題は面積や角度を求めてきましたが、
今回は比を使うような問題です。でも安心してください。
ヒントを見ればすぐにわかりますので一緒に見ていきましょう。
相似比は対応する辺の比
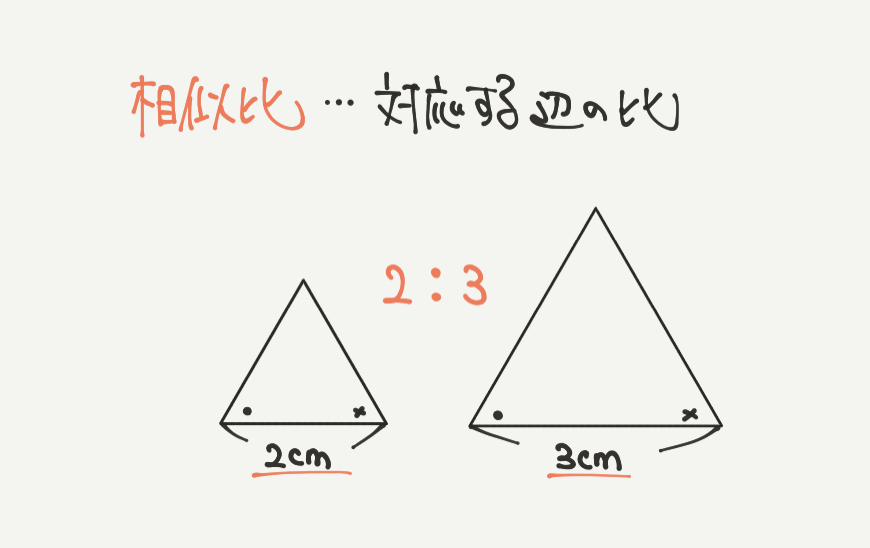
今回の問題ではいろいろな言葉が出てきますので、その意味を確認しておきましょう。
たとえばお互いに相似な2つの三角形があるとすると、
相似比は2cm:3cm=2:3になります。
相似比は対応する辺の比なので、2cmと3cmを使って比を出していきました。
面積比(表面積比)は相似比の2乗
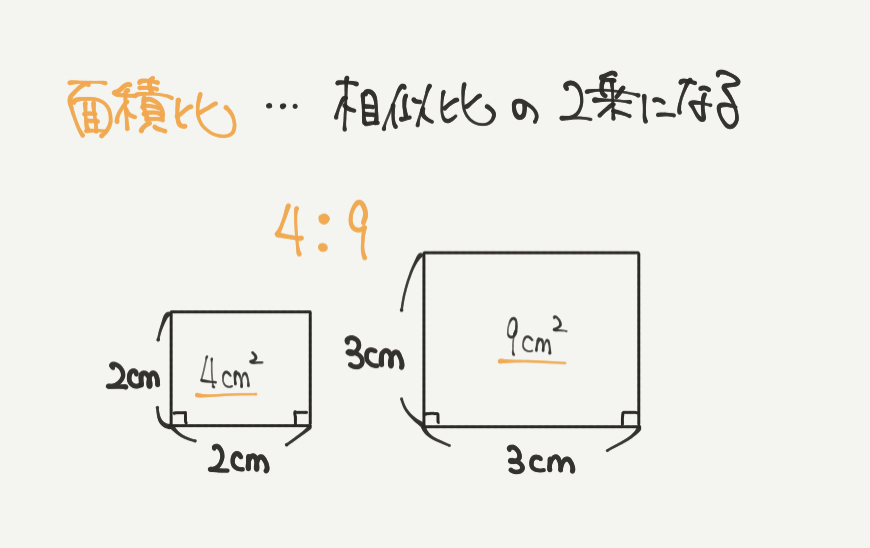
一方で面積比は辺(たて)×辺(横)で求めることができますので、
相似比の2乗が面積比、表面積比になります。
上の図では相似比が2:3の図形の面積(表面積)を求めています。
すると2×2:3×3=4:9になることがわかります。
体積比は相似比の3乗
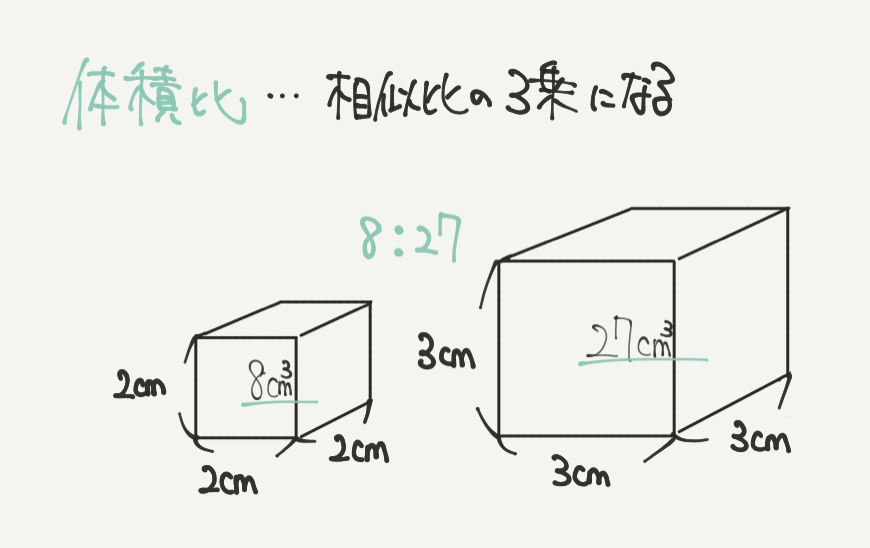
最後に体積比についてみていきます。
相似比が2:3の立方体があるとします。
すると面積比は、2×2:3×3=4:9になり
体積比は2×2×2:3×3×3=8:27と考えることができました。
少し考えればわかるので、暗記して覚える必要はないですね!
今回の問題はこれだけ分かっていればすぐに解けますのでサクサク進めましょう。
問題に挑戦!
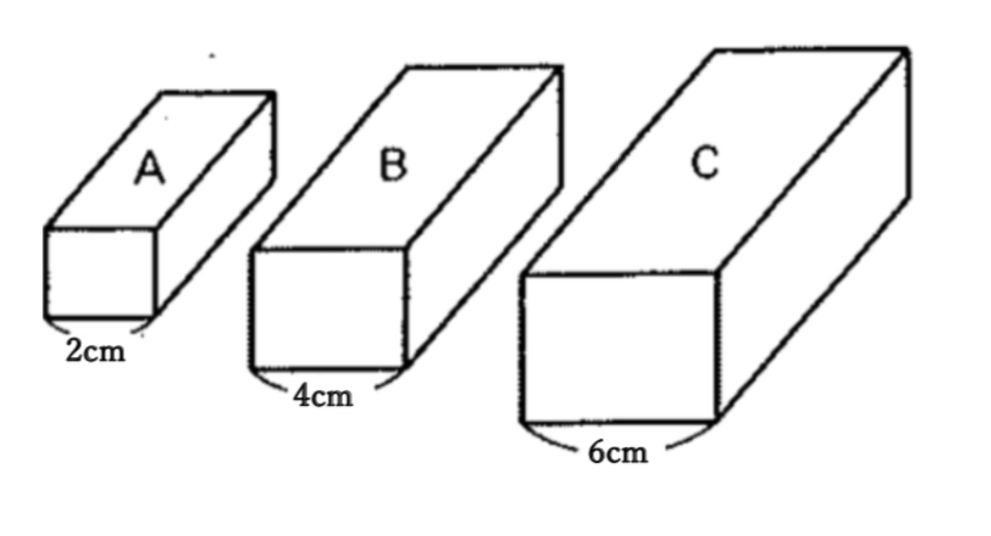
解答
答えを見るにはここをクリック!
①1:2:3
②1:4:9
③1:8:27
この記事を書いている人はこんな人


解説を見てみよう!
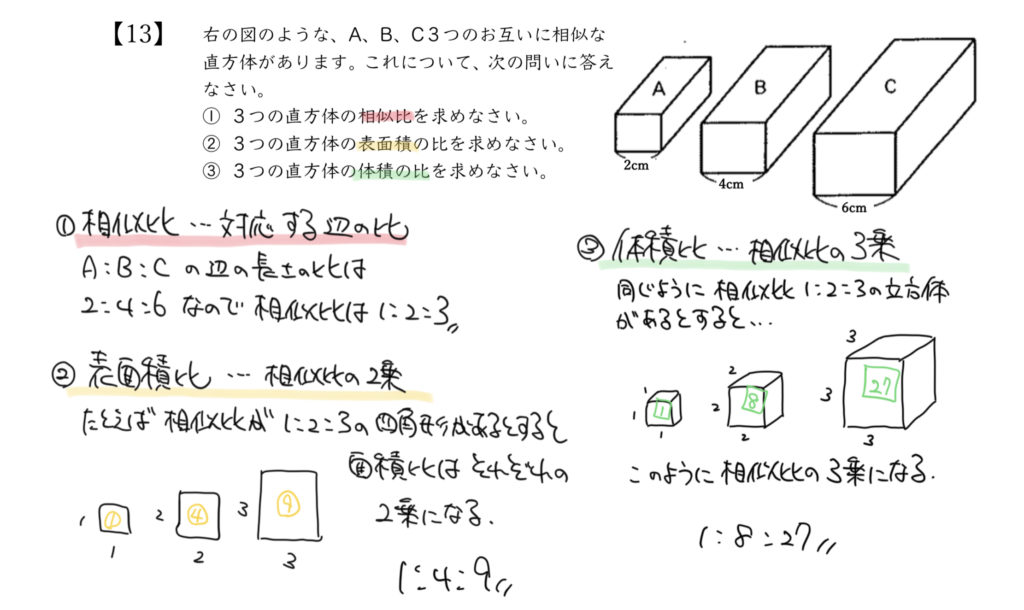
STEP1:今回の図形は互いに相似な図形
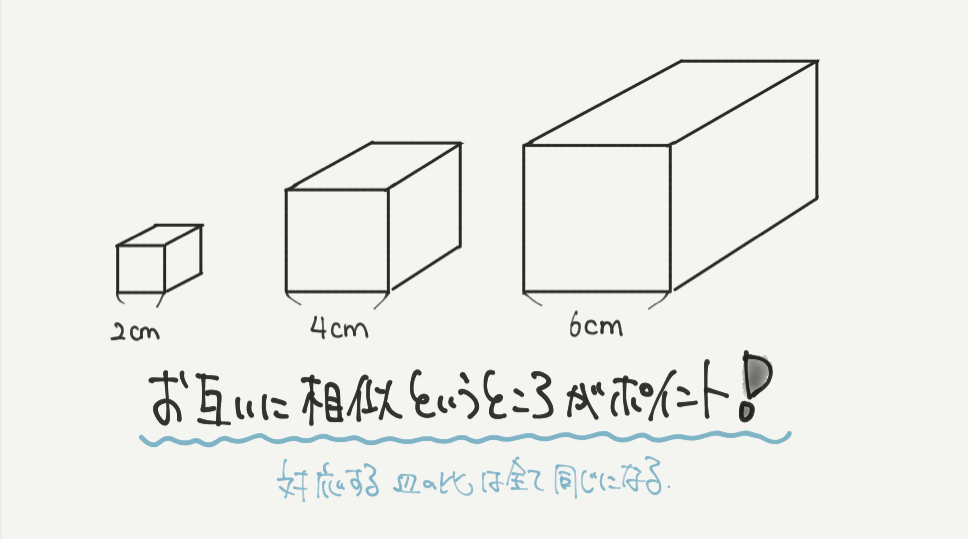
まずは問題文の内容をきちんと理解しましょう。
かんたんそうに見える問題も、まずは内容を正しく確認することが大事です。
今回の図形は全て互いに相似な図形と言われているので、
対応する辺の比は全て同じであることがわかると思います。
STEP2:相似比を求めよう
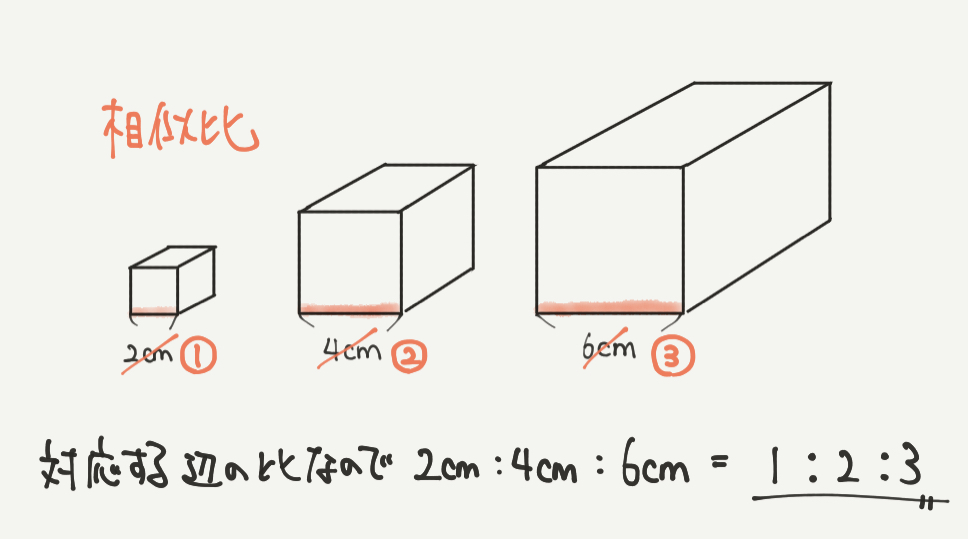
まずは相似比から求めましょう。
相似比は対応する辺の比ですので、
2cm:4cm:6cm=1:2:3となります。
「えっ?これだけ?」と思うかもしれませんが、
こういう問題が言葉の意味を知っていたらすぐに解けるようなラッキー問題です。
なのできちんと言葉の意味を理解しておきましょう。
STEP3:表面積比を求めよう
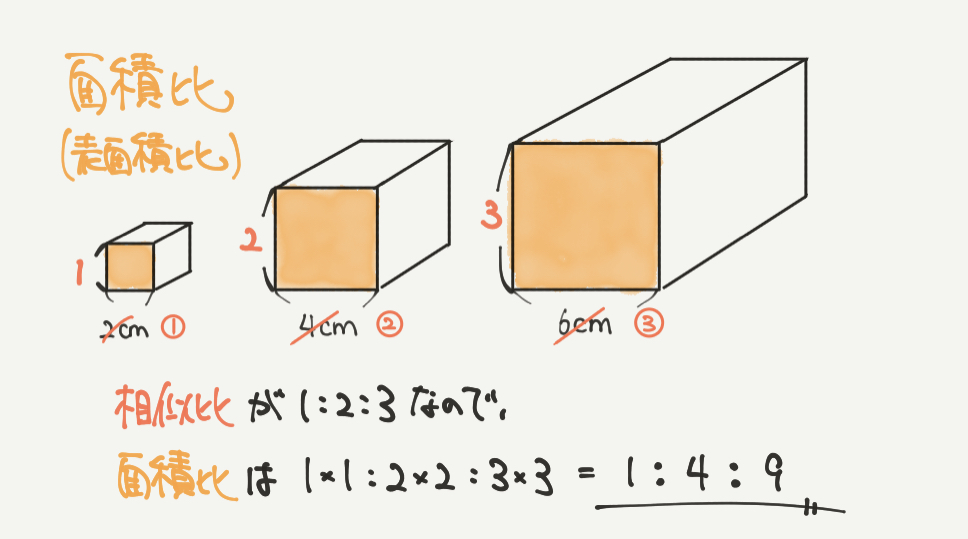
表面積比は面積比と考え方は同じです。
それぞれの立体の面積比は、相似比1:2:3から
1×1:2×2:3×3=1:4:9になります。
たとえば表面積であっても1つの面の面積を6倍するだけなので、
1×6:4×6:9×6=1:4:9と答えは同じになることがわかりますね。
STEP4:体積比を求めよう
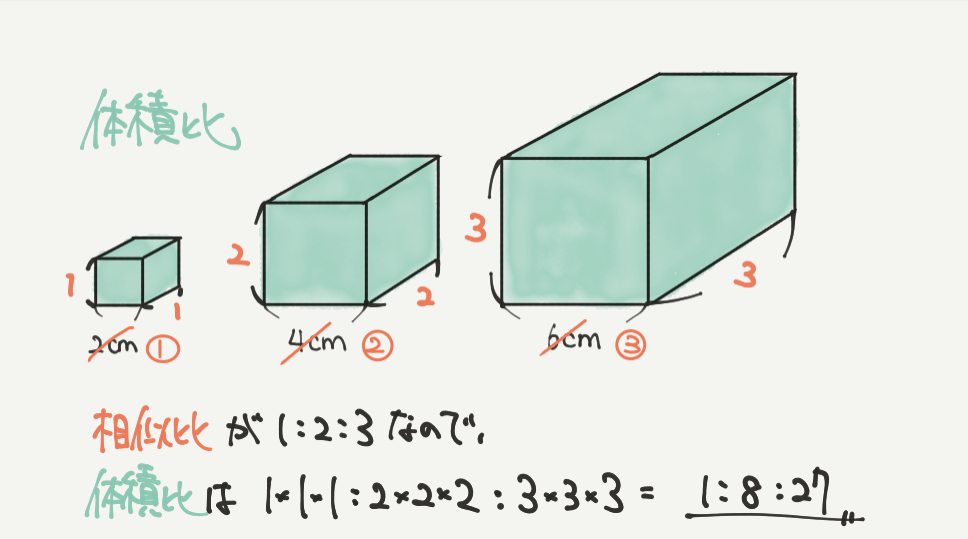
最後に体積比です。
これもむずかしいことはなく、相似比1:2:3から
1×1×1:2×2×2:3×3×3=1:8:27となりました。
これは3つの図形が互いに相似な図形だから成り立ちました。
どんな図形でもこのような体積比になるわけではないので注意しましょう。
相似比と表面積比と面積比を求める問題の解説
今回の問題で大事なポイント
- 相似比の考え方(はじめに、STEP2)
- 面積比の考え方(はじめに、STEP3)
- 体積比の考え方(はじめに、STEP4)
今回の問題は相似比と表面積比と体積比の基本を知っていればすぐに解ける問題でしたね。
繰り返しの説明になりますが、
相似比:対応している辺の比です。
今回AとBとCの横の辺が対応しているので2:4:6となり1:2:3になります。
表面積比:辺の比が1:2:3ならば、面積は一辺×一辺になるので1:4:9になりますよね。
よって表面積比も相似比の2乘になります。
体積比:体積を求めるには辺を3回かける必要がありましたね。
図からもわかるように、体積比は相似比の3乗になります。よって1:8:27となりました。
 わかみや先生
わかみや先生この問題は知っていればすぐに解けますので、
言葉の意味を正しく理解してきちんと復習しておくようにしましょう!