はじめに
さて、今回は和差算のなかでもよく出てくる速さの問題にチャレンジしていきましょう!
この問題は出てくる登場人物の進む速さが途中で変わってしまいます。
速さが変わってしまうと、計算が少し大変です。
でも安心してください。
速さが途中で変わってしまうような問題も、面積図を使うことで簡単に解けるようになりますよ!
そして面積図を書く以外にも大事な考え方があります。
それが仮定すること、です。
仮定する、というのは「もし○○が□□だったら〜」というように問題を解きやすくするための考え方の一つです。
速さの問題で仮定の考えを使うと「もしこの人が速さを途中で変えないで、ずっと一定の速さで走っていたらどうなるのだろう」と考えることです。
この仮定する考えを使って、問題を解く練習をしてみましょう。
例題に挑戦!
これを面積図ともし〜だったらという仮定を使って解きます。
さあ解いてみましょう!
解答
1時間
解説を見てみよう!
左の図が問題文をそのまま面積図にしたときです。
そして右の図が「もしこの人がずっと時速20kmで走ったらどうなるか?(40km走れちゃうじゃん!)」という図になります。
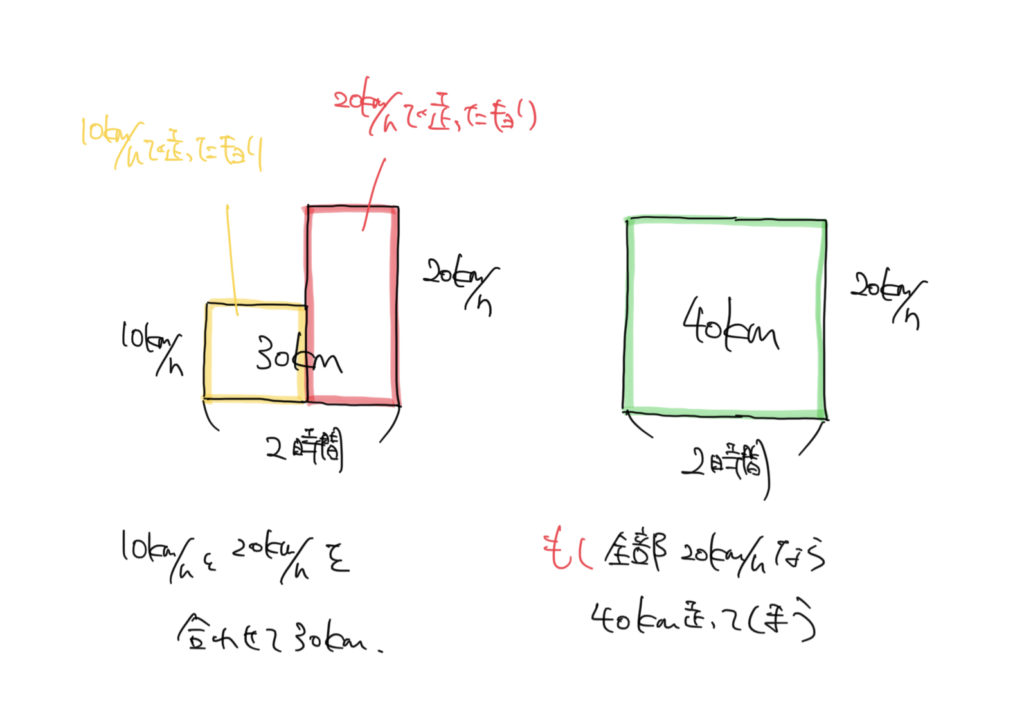
この2つの図形を重ねて比べると、足りない部分の面積が
40km-30km=10km
と求めることが出来ます。
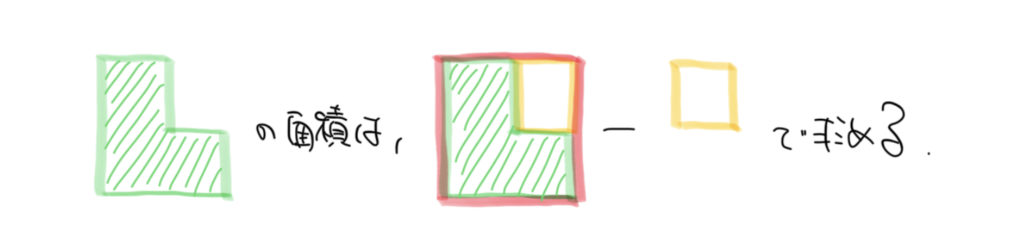
上の解説のように四角形を重ねて10kmの面積を出しましょう。
差の四角形の面積(黄色)が10kmとわかります。
たての長さは速さの引き算をすればいいので、
20km/h(時速20km)-10km/h(時速10km)=10km/h(時速10km)
となるので歩いた時間(横の長さ)は
10km(面積)÷10km/h(たての長さ)=1時間(横の長さ)
歩いた時間は1時間と求めることができます。
さあ、どうでしたでしょうか。
ここまで面積図がしっかりかけて、初めて正解にたどり着きます。
ちなみに式だけでも解けちゃいますが、
しっかり図を書かないと思わぬところでミスをしてしまうので気をつけるようにしましょう。
面積図の詳しい書き方は解法別のカテゴリーから面積図をクリックしてください!
そして中学受験の算数では面積図のほかに、この仮定する考えも非常に大切になります。
今のうちから覚えておきましょう!
問題に挑戦!
解答
答えを見るにはここをクリック!
16km
解説を見てみよう!
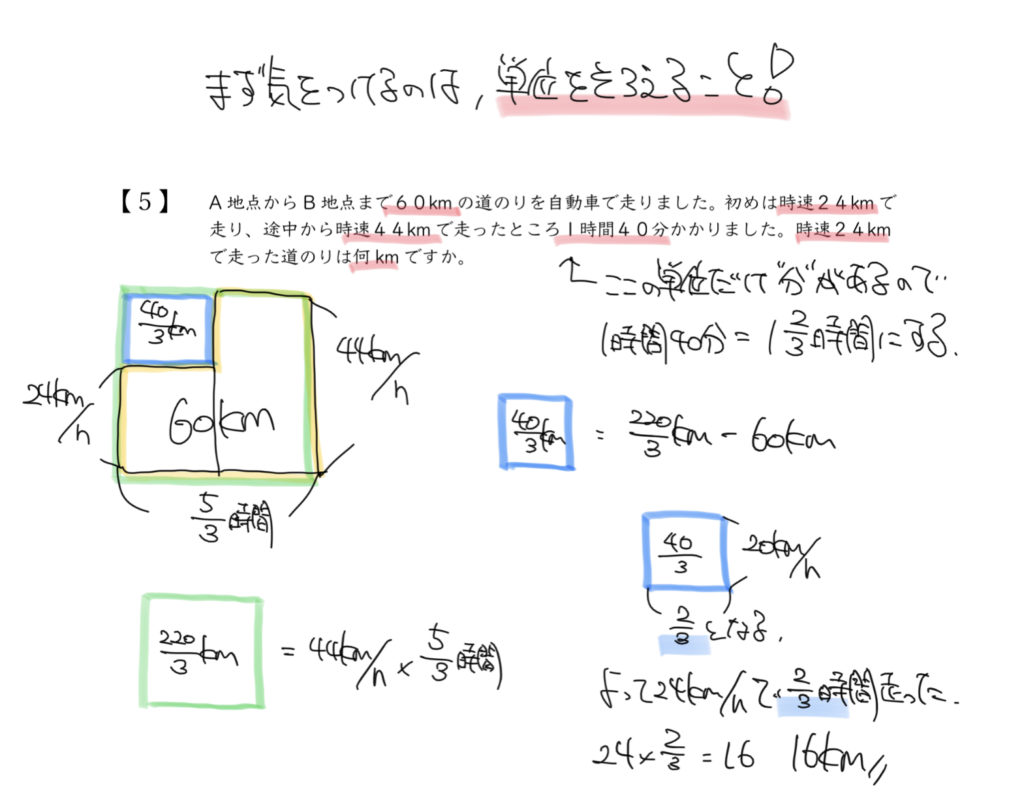
問題文から速さの面積図はこのように書くことができます。
まずはこの図をきちんと書けたかを確認しましょう。
この図が書ければ最初のステップはOKです。
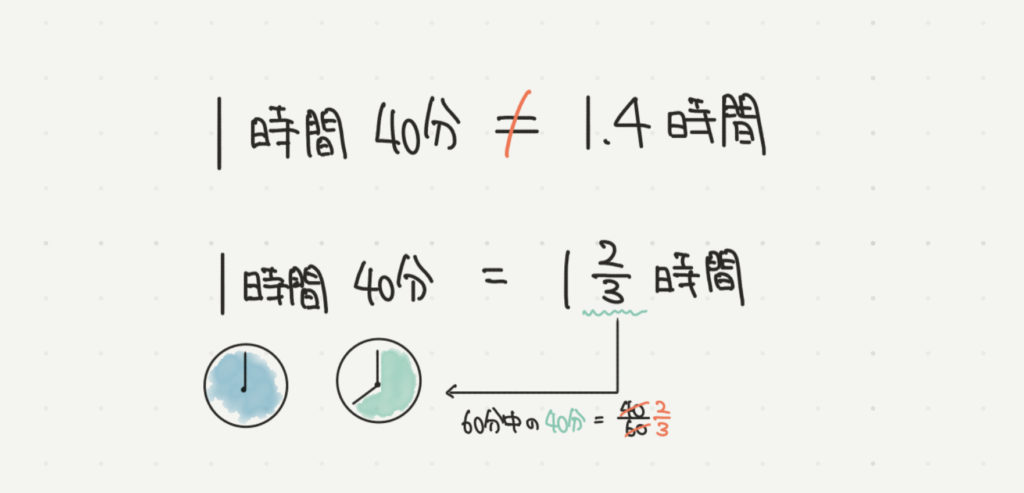
今回の問題は単位が時速(1時間で進む距離)なので1時間40分も“○時間”で統一する必要があります。
60分=1時間なので
40分=2/3時間になります。
よって1時間40分=5/3時間と書くことができます。
1時間40分だからといって1.4時間とかにしないこと!!

そして面積図が書ければ次は仮定して、問題を解きやすくしてみましょう。
もしこの自動車が時速44km(44km/h)で5/3時間(1時間40分)走ったらどうなるのか、
それを面積図にしたのが緑の四角形の図です。
緑の四角形の面積は44km/h(たて)×5/3時間(横)=220/3km(緑の四角形の面積)となります。
しかし実際に走った距離は60kmなので、
青色の四角形の面積を
220/3km-60km=40/3km
と求めることができます。
そこから計算すると横の長さ(走った時間)は
40/3km(面積)÷20km/h(たて)=2/3時間(横)
よって時速24km(24km/h)で走った時間が2/3時間とわかります。
ここから答えが
24km/h(たて)×2/3時間(横)=16km(面積)
16kmと求めることができます。
算数を得意にするコツ
 わかみや先生
わかみや先生速さの問題では面積図をきれいに書くことが大事なポイントでした。
まずは問題文からきちんと図を描けるような練習をしていきましょう。
そして面積図が書ければ、そこから仮定の考えを使って大きな四角形を作りましょう。
大きな四角形と小さな四角形たちを比べて問題を解いていくやり方が大事でした。
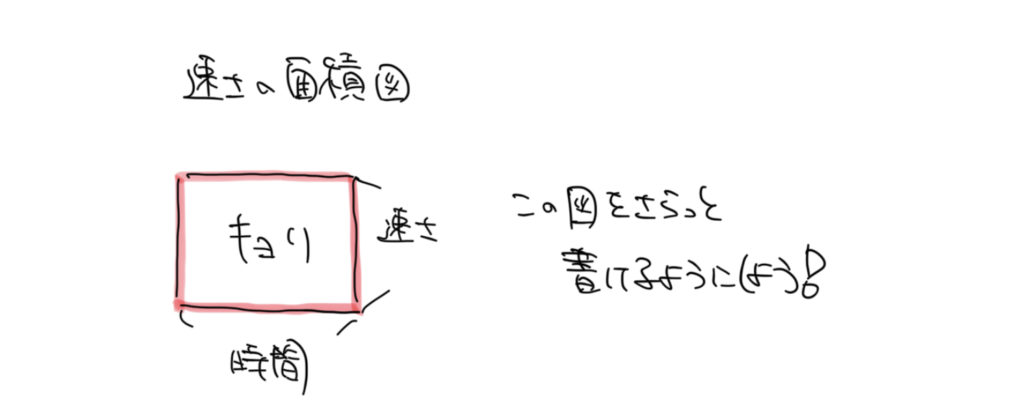
ちなみに速さの面積図は下のように書くことができました。
今後も使うので慣れておきましょう。

そしてもう一点、算数を得意にするコツがありました。
それが単位をそろえる、という考え方です。
算数や数学の苦手な受験生の典型的なまちがいとして、
単位をごちゃ混ぜにして考えてしまうというものがあります。
例えば今回の問題なら、
時速44kmで1時間40分走ったのに
44×1.4(1時間40分?)にしてしまったりするとまちがった計算をしてしまいます。

そのような単位をそろえる練習をして、問題を解いていきましょう。
類題は次のページから!!