はじめに
みなさんこんにちは!
今日は「割合と比」の中でも、同じ部分のところから全体の長さの比を求めるという問題を解いていきましょう!!
みなさんと一緒に勉強するこの問題は今までよりも、少しむずかしいです。
きちんと例題を見て、問題に取り組んでいきましょう。
まずは例題に挑戦だ!
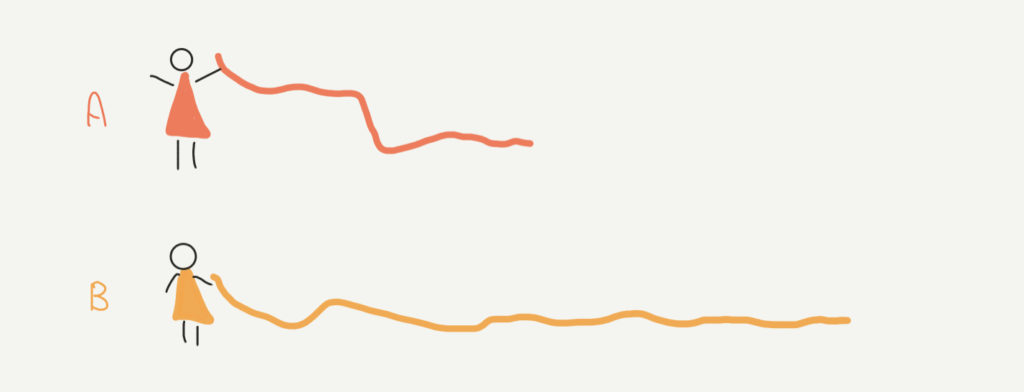
↓すぐ下に解答があるから見えないように気をつけてね!
解答
A:B=1:2
解説を見てみよう!
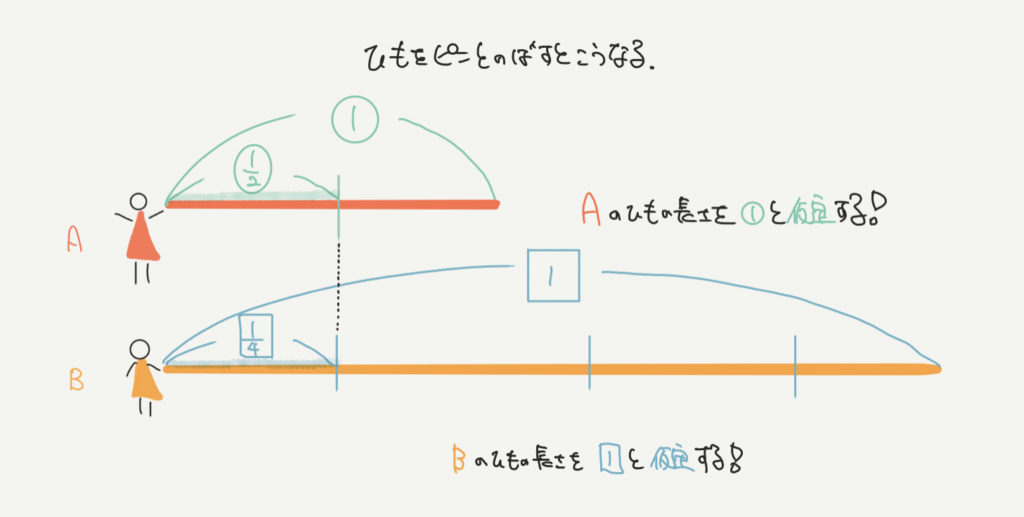
Aのひもの長さを①、Bのひもの長さを□の1と仮定すると、上の図のようになります。
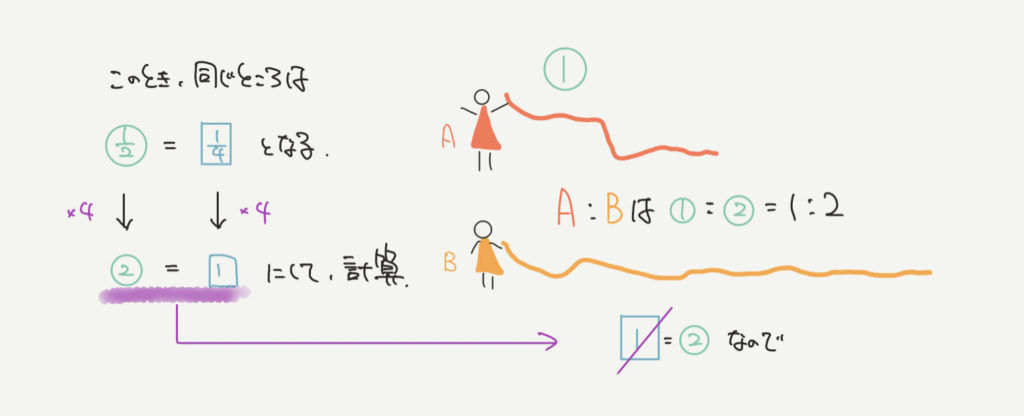
問題文から、○の1/2=□の1/4が同じであることがわかると思います。
○の1/2=□の1/4なので、両辺を4倍すると…!
②=□の1 となります!
ここから記号を統一しましょう。
記号を統一するとは、どういうことかというと、○と□の2つの記号を1つにまとめることです。
今回の問題は②=□の1 とわかっているので、Bのひもの長さ(□の1)を②とかき直すことができますね!
よってAとBのひもの長さの比は、
①:②=1:2 とわかります!!
ウラワザ解説
ここからはウラワザ解説です。これを知らなくても問題は解けます。
でも!このやり方を知っていると、問題を解く時間がグッと短くなります。
行きたい学校があるなら、ここもきちんと勉強しておく方がいいと思います。
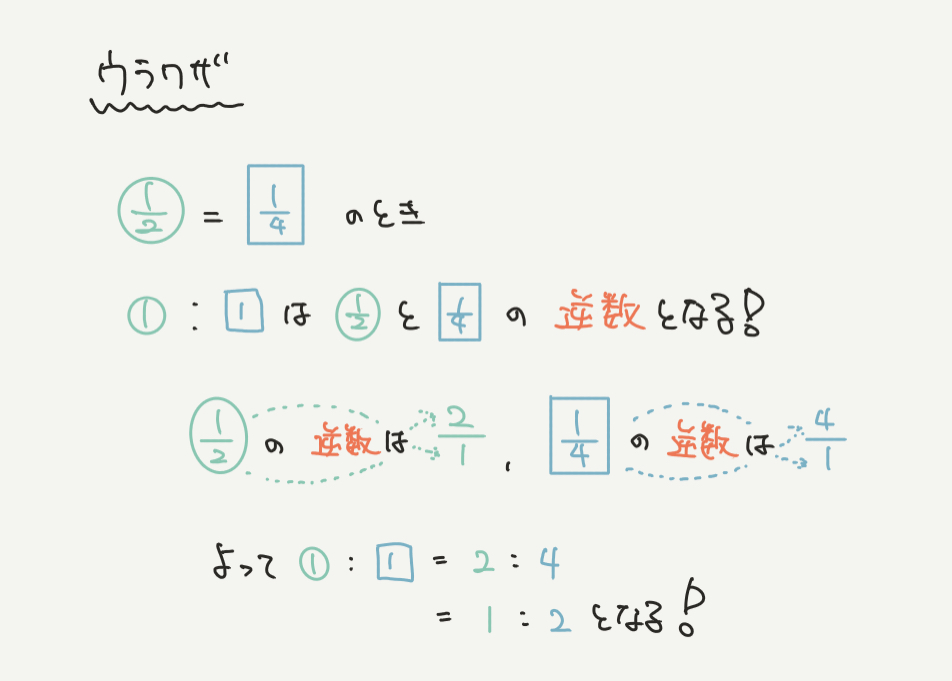
ウラワザとは、
○の1/2=□の1/4のとき、
①:□の1は1/2と1/4の逆数になるということです。
 わかみや先生
わかみや先生はい、意味がわからないですよね笑
大丈夫です!
まず逆数について勉強しましょう。
逆数とは?
逆数とは、ある分数の分母と分子をいれかえた数になります。
なので、1/2の逆数は2/1=2になりますし、1/4の逆数は4/1=4となります。
話をもとにもどします!!
○の1/2=□の1/4のとき、①:□の1の値は、1/2と1/4の逆数になる、つまり
2:4=1:2になります。
いかがでしたか?
これらを理解した上で、実践問題に挑戦していきましょう!
問題に挑戦!
解答
答えを見るにはここをクリック!
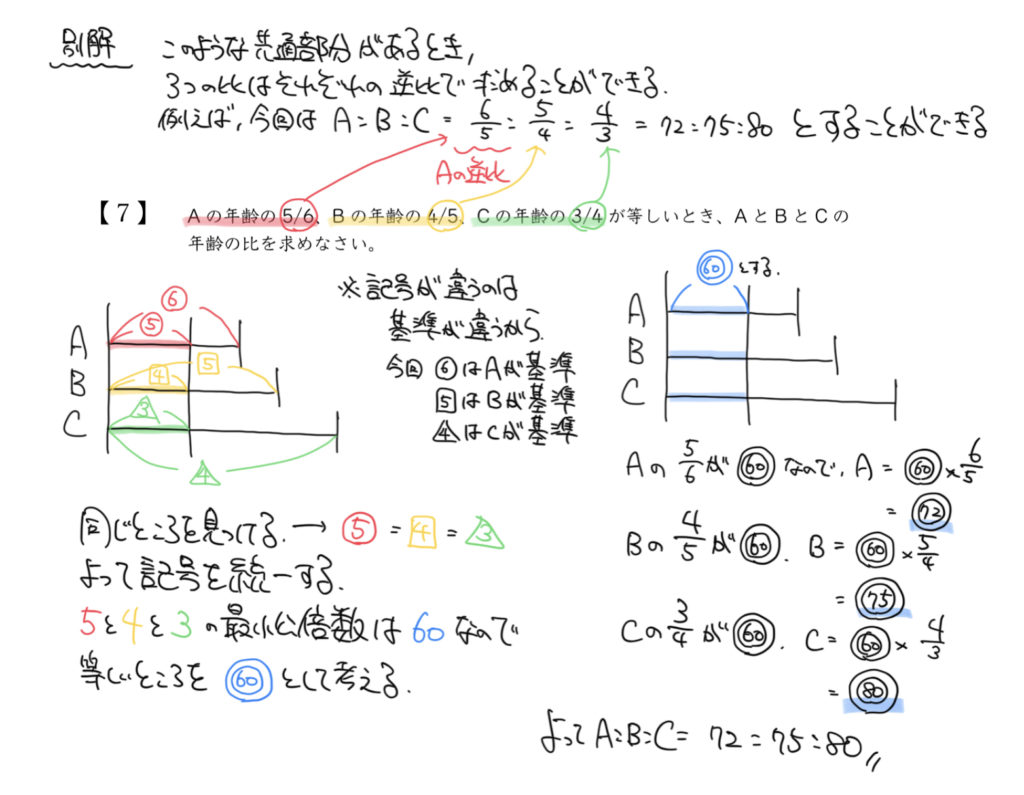
72:75:80
この記事を書いている人はこんな人



解説を読んで「 割合と比 」を攻略しよう!

STEP1:問題文を図にして同じところを見つけよう
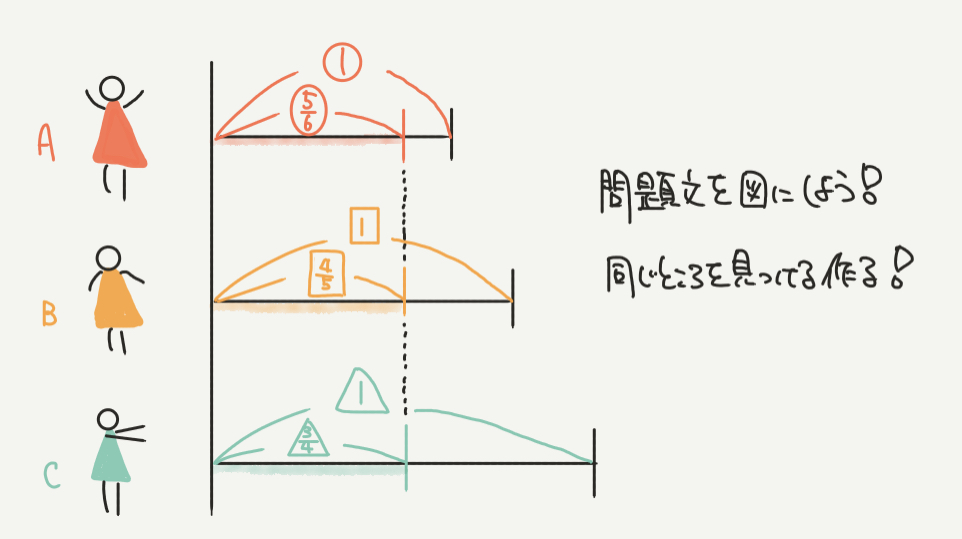

まずは線分図を書いて、問題文の内容を正しく理解しましょう!
ちなみに、間違って書いてしまっても正解できるので大丈夫ですが、
今回はAの年令が一番低く、B、Cの順番で年令が高くなっています。
問題文を図にして、まずはこの点に注意してください。
たとえば、きちんと図を書くことができればABCの答えが出たときにケアレスミスしていないか確認することができます。
↑Aが一番年下のはずなので、A:B:C=3:2:1とかになってたらおかしいですよね??
ここからウラワザに行ってもいいですが、一旦は普通のやり方で進めていきましょう。
STEP2:同じ部分を◎の1と仮定してみよう

さあ、ここから同じところを探しましょう!
探すまでもなく、問題文で教えてくれていますね!
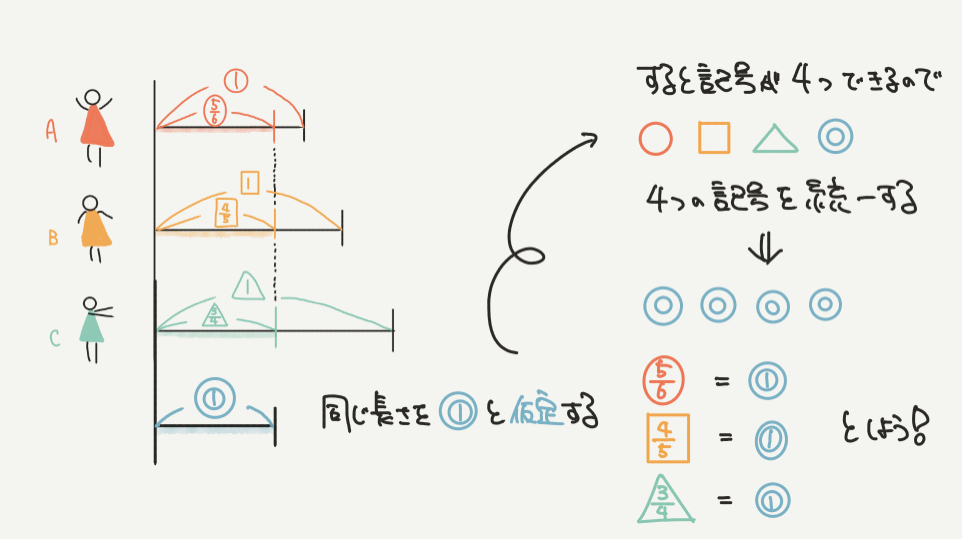
はい、今回は○の5/6、□の4/5、△の3/4が同じであるとわかります。
ですのでここの部分を◎の1と仮定して考えていきましょう。
大事なのは例題でも教えましたが、記号を一つずつ減らしていくことです。
この4つの記号を統一していきましょう!!
STEP3:記号を1つに、計算していこう!
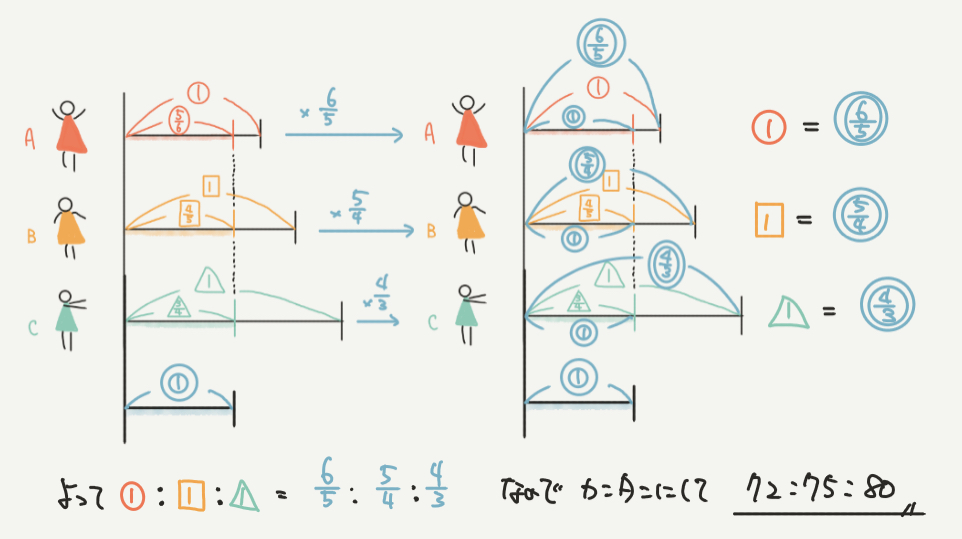

○の5/6、□の4/5、△の3/4を◎の1ですので、それぞれの記号を◎で表してみましょう。
Aの年令を求めよう!
○の5/6=◎の1なので、両辺を6倍して
⑤=◎の6となります。
最後にこれを5で割って、
①=◎の6/5と求めることができました!!
Bの年令を求めよう!
□の4/5=◎の1なので、両辺を5倍して
□の4=◎の5となります。
同じようにこれを4で割って、
□の1=◎の5/4と求めることができます。
Cの年令を求めよう!
△の3/4=◎の1なので、両辺を4倍しましょう!
もういけますね??
△の4=◎の3となります。
これを3で割って、
△の1=◎の4/3と求めることができますね。
最後は計算あるのみ!
最後は、これらの比を出すのみです。
○の5/6:□の4/5:△の3/4=◎の6/5:◎の5/4:◎の4/3なので、両辺を5、4、3の最小公倍数の60倍しましょう。
すると、①:□の1:△の1=72:75:80となりました。
ウラワザ:逆数を使って解いてみよう
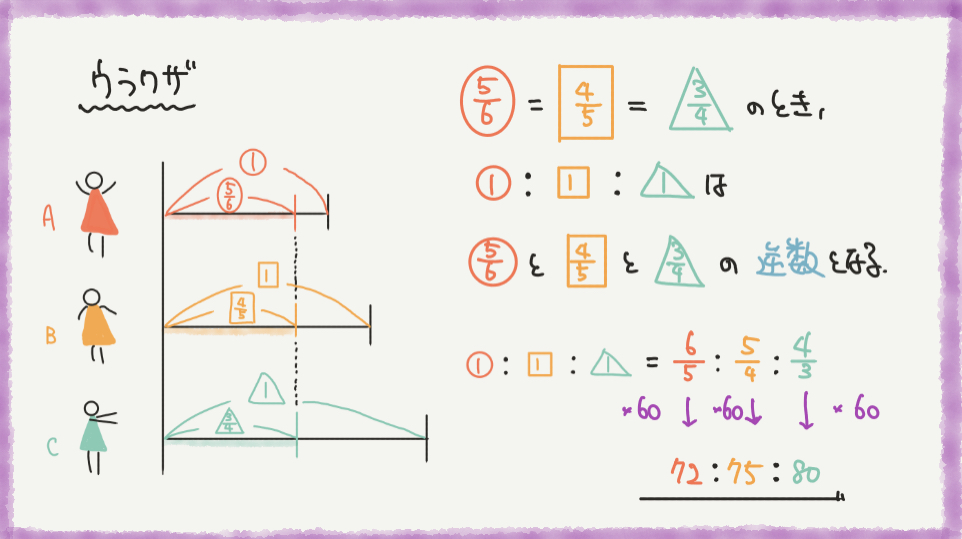
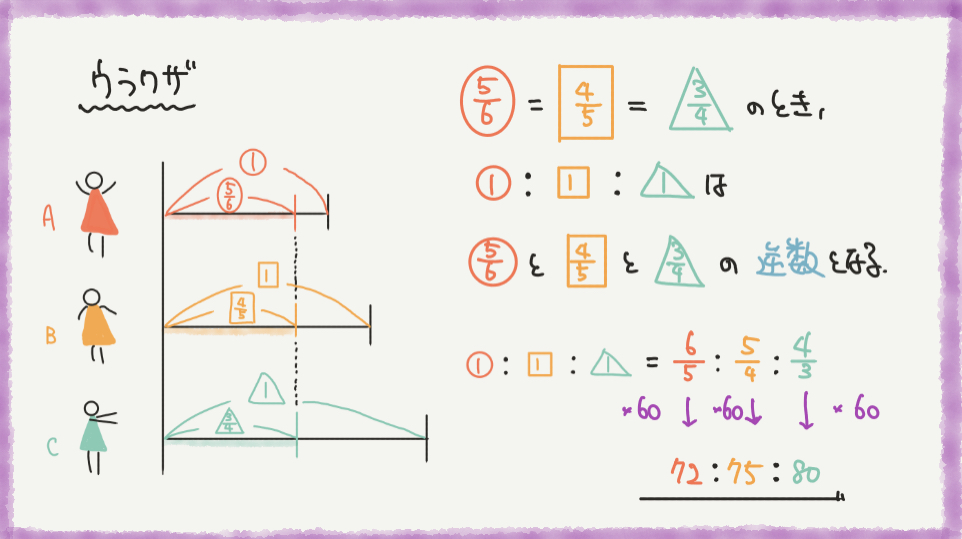
先ほど教えたウラワザを使うと、STEP1からカンタンに解くことができました。
今回はAの5/6、Bの4/5、Cの3/4が等しいので、
逆数の6/5:5/4:4/3=72:75:80となります。


また1点注意してほしいところですが、線分図を書くときに同じ記号でグラフを書かないように注意しましょう。
↑たとえばA 、B、Cの年令を同じ記号「○」だけで表さないようにしましょう!


共通している部分の割合から全体の比を求める問題のまとめ
今回の問題で大事なポイント
線分図の書き方(STEP1)
・きちんと問題文の内容を図を書いてみよう
・「同じところを見つける、作る」考え方
逆数のウラワザを使いこなそう
仮定の考え方(STEP2)
・もし○○が□□だったら〜と考えましょう
以上で今回の問題は終わりです!おつかれさまでした〜!!
いつもの問題と比べて少しむずかしかったと思いますが、理解できましたでしょうか。
わからないポイントはありましたか?
もしあればコメントで書いてくださいね。
↑なるべく回答できるようにがんばります!!
この問題では、
①線分図をきちんと書くこと
②逆数のウラワザを使えるようになること
③仮定の考え方を使うこと
が大事でした!!
復習しておきたい受験生は下のリンクから問題に挑戦してみてくださいね!
線分図の問題の復習!
2教科の点数の割合からそれぞれの点数を求めるには?


仮定の考え方を使う問題の復習
親子の年令の比からある年数を求めるには?