はじめに
みなさんこんにちは!!今日もよろしくお願いします!
それにしても最近とても寒くてかぜひいちゃいました💦
たしかに最近急に寒くなってきましたね。体調管理も受験対策の1つですので、
受験生のみなさんはかぜを引かないように暖かくしてくださいね。
今日は「平面図形」の中でも円が出てくる問題です。
むずかしそうに見えますが、実はとってもかんたんな問題なのでサクサク解いていきましょう!
まずはいつも通りヒントから説明します〜。
「同じところを見つける、作る」考え方の復習
まずは面積が同じ図形が重なっているときの考え方についておさらいしましょう。
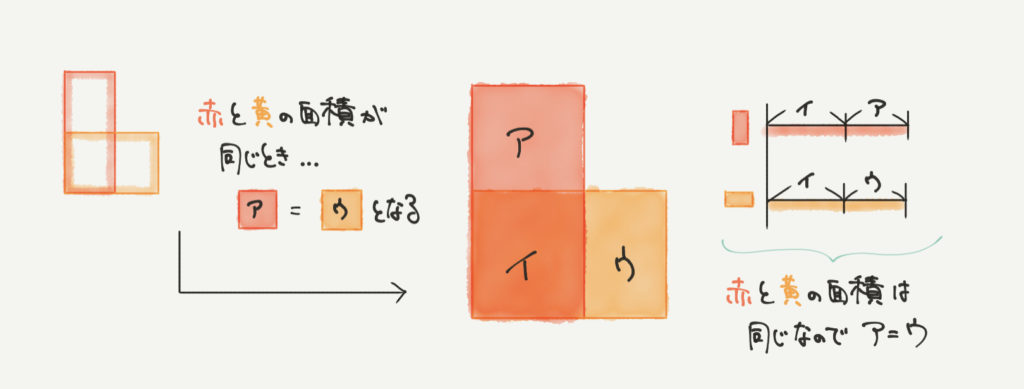
たとえばここに赤い四角形と黄色い四角形が重なっているとします。
赤い四角形と黄色い四角形、どちらの面積も同じです。
このとき、2つの図形のアの部分とウの部分の面積が同じになります。
なぜ同じになるのかは線分図を見てもらえばわかると思います。
赤い四角形:ア+イ
黄色い四角形:ウ+イ
となりますので、右のように線分図を書くことができます。
イの部分はどちらの図形にもあるから、比べる部分はアとウだけでいいってことだね!
今回の問題で問題でおさえておいてほしいポイントはこちらだけです!
 わかみや先生
わかみや先生ここさえ分かってしまえばあとはサクッと問題が解けるはず!
さっそく解いていきましょう。
問題に挑戦!
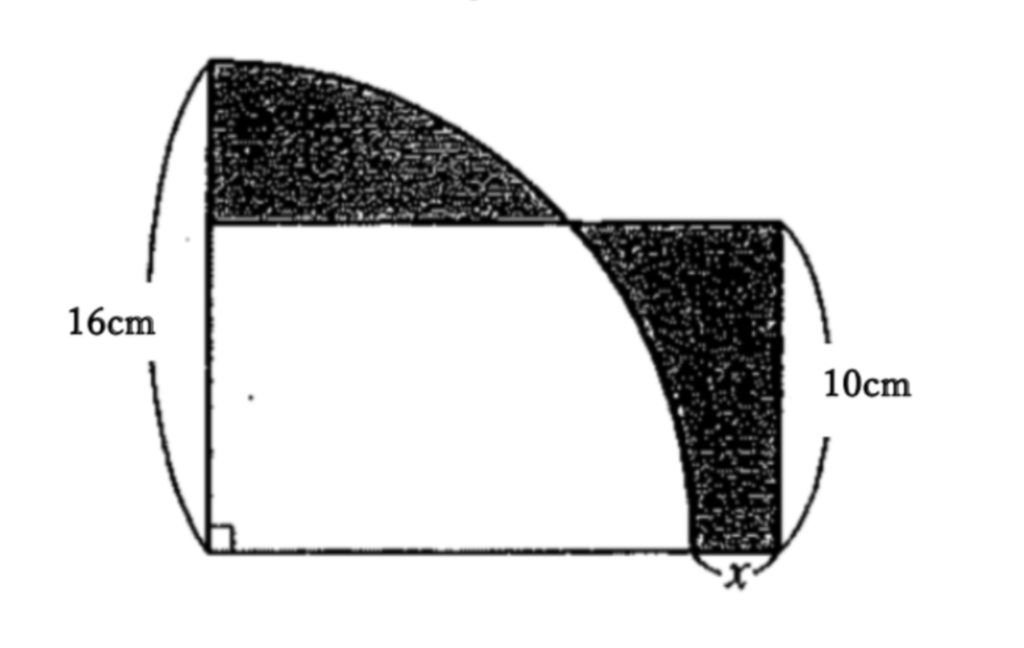

解答
答えを見るにはここをクリック!
4.096cm
この記事を書いている人はこんな人




解説を見てみよう!

STEP1:問題文から同じところを見つけよう
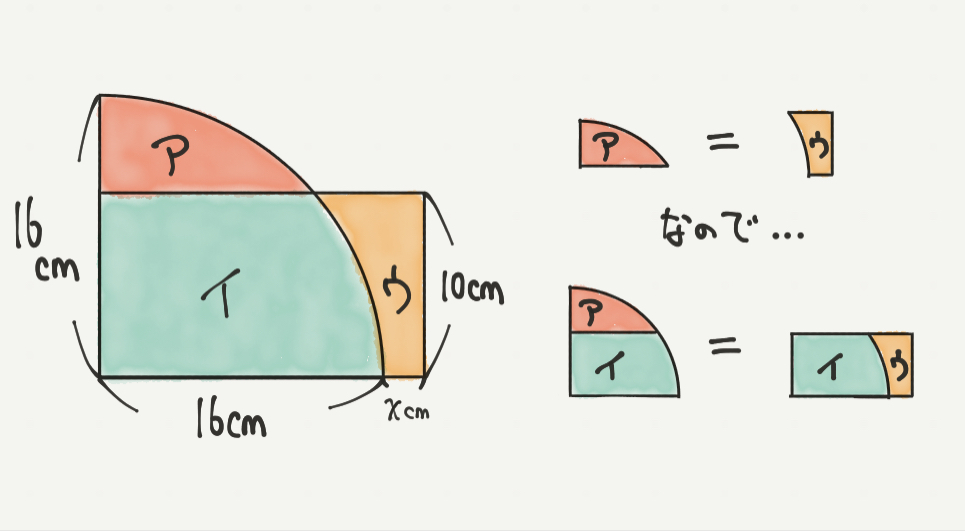

STEP1ではいつも通り、問題文の内容をまずは図にしていきます。
今回の問題文から、アとウの面積が同じだということがわかります。
そしてアとウのほかにイにも注目してもらうと、
四分円(ア+イ)と長方形(ウ+イ)の面積が同じであると考えることができます。
イの面積はアとウのどっちにも足されるから、
ア=ウならア+イ=ウ+イになるね!
STEP2:四分円と長方形の面積を確認しよう
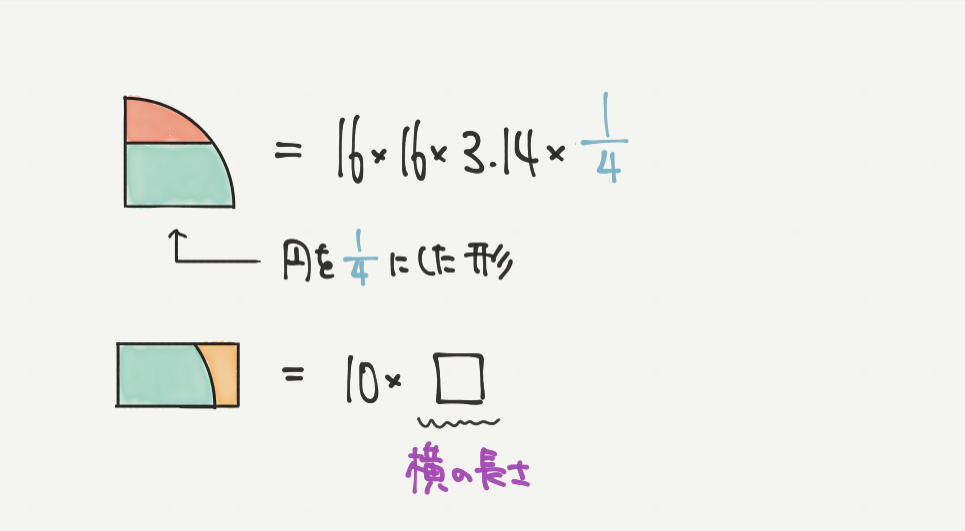
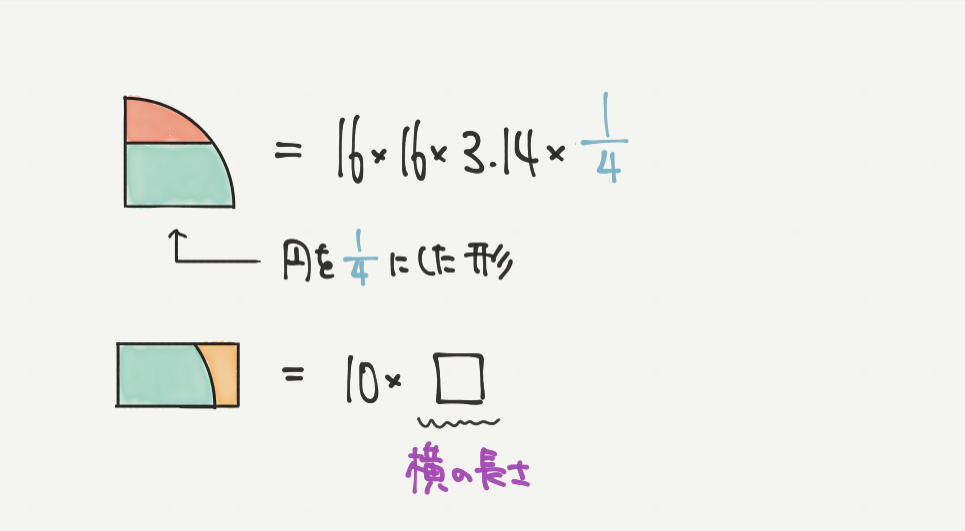
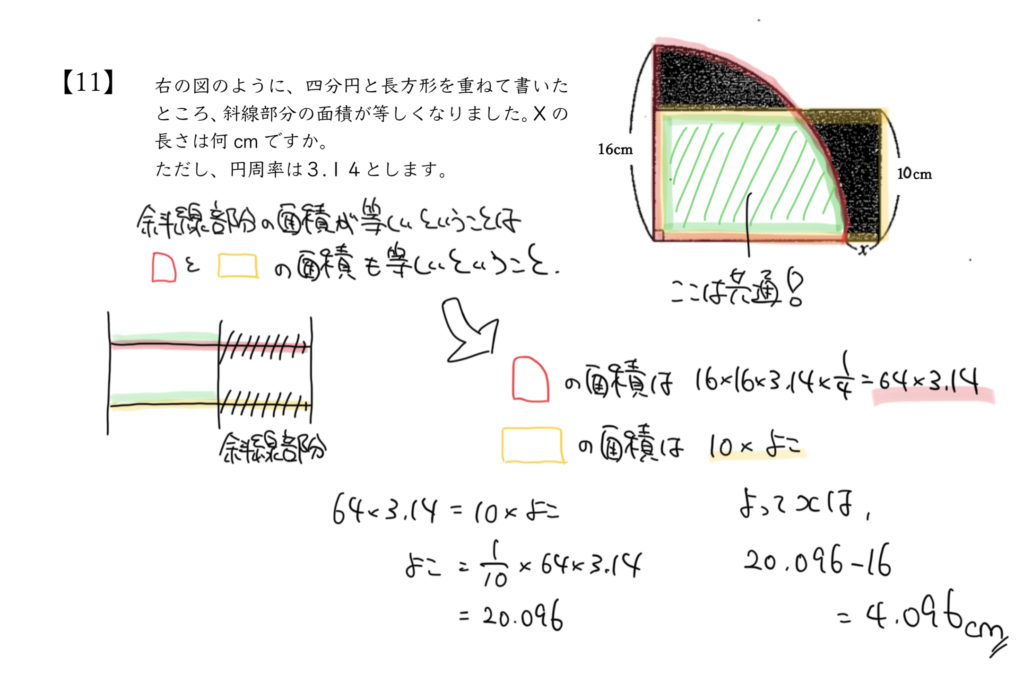
STEP1から四分円(ア+イ)と長方形(ウ+イ)の面積が同じということがわかりました。
なので、それぞれの面積を考えてみましょう。
四分円(ア+イ):16×16×3.14×1/4
長方形(ウ+イ):10×□
になりますね。
よって求めたい答えは長方形の横の長さ(□)から16cm(円の半径)を引いた数になります。
STEP3:長方形の横の長さを計算しよう
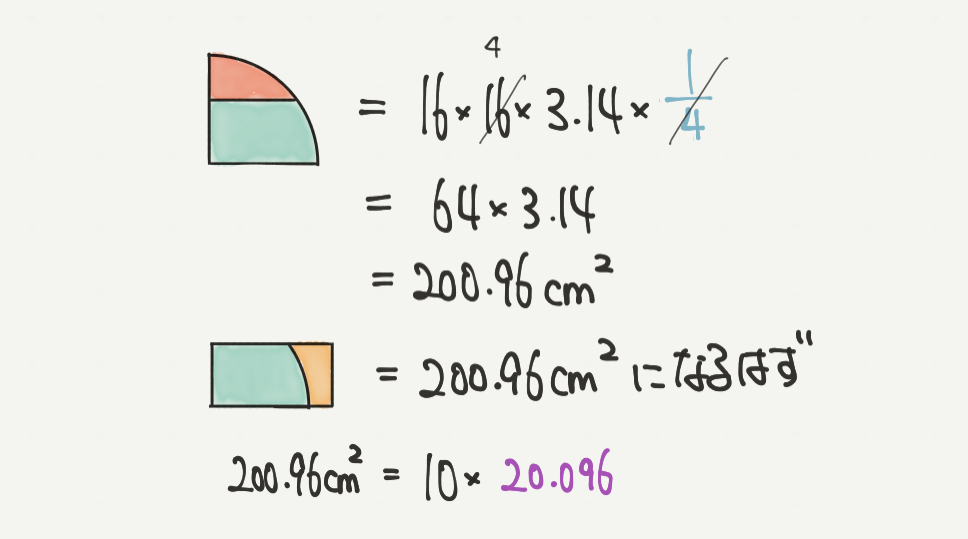
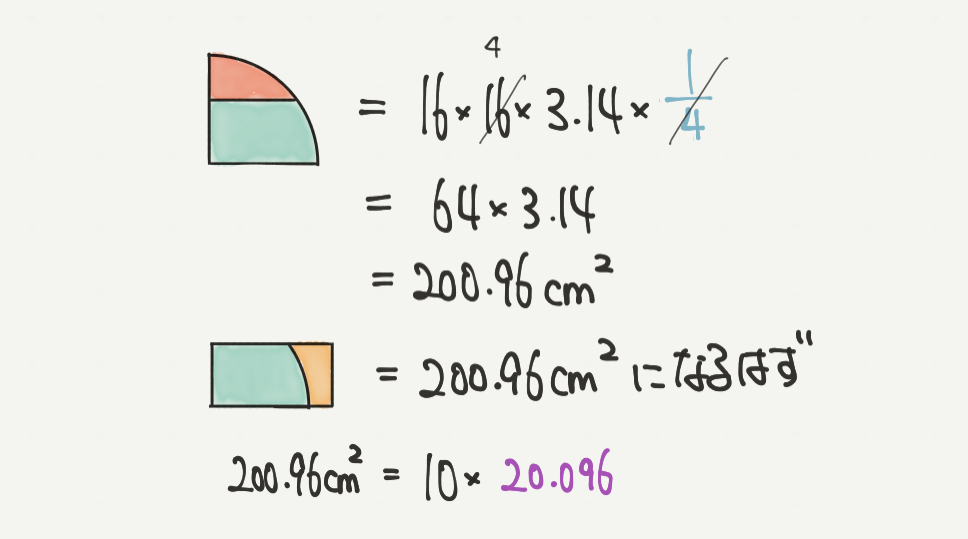
STEP3はSTEP2の続きです。
四分円(ア+イ):16×16×3.14×1/4
長方形(ウ+イ):10×□
をそれぞれ計算しましょう。
四分円(ア+イ)
=16×16×3.14×1/4
=64×3.14
=200.96㎠
と計算できました。
そして問題文から、長方形(10×□)の面積も同じく200.96㎠ということがわかるので
横の長さは、200.96㎠÷10=20.096cmになります。
STEP4:求めたい答えを出そう
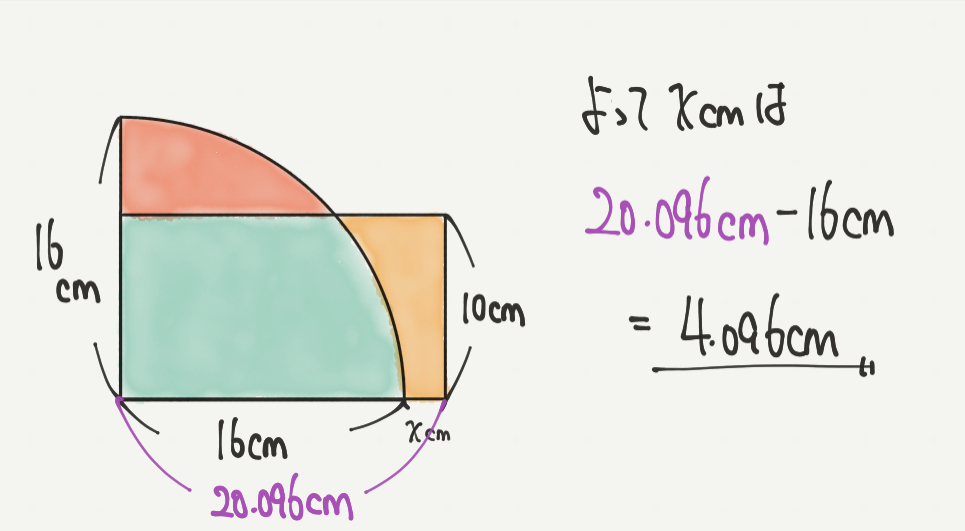

最後は計算して答えを出していくだけです。
今回の問題で知りたい長さは、長方形の横の長さ(□)から16cm(円の半径)を引いた数でしたね。
STEP3で長方形の横の長さ(□)が20.096cmと求まりましたので、
答えのxcmの長さは、
x cm
=20.096cm-16cm
=4.096cmになりました!
重なった四分円と長方形から長さを求める問題のまとめ
今回の問題で大事なポイント
- 「同じところを見つける、作る」考え方(はじめに、STEP1)
- 円についての考え方
・ 四分円の面積の求め方の確認(半径×半径×3.14×1/4)
以上で今回の四分円と長方形の重なった問題は終わりです!
いかがでしたでしょうか?
今回の問題のポイントは「同じところを見つける、作る」考え方でした。
問題文で斜線部分(アとウ)の面積が等しいということは
線分図より、四分円(ア+イ)と長方形(ウ+イ)の面積も等しいということでしたね。
「同じところを見つける、作る」考え方は「さんすうがく」の問題でもたくさん出てくる大切な考え方です。
復習したい受験生は時間があれば下の問題にも挑戦してみてくださいね!
「同じところを見つける、作る」考え方の復習
商品の個数と金額の差から買った商品の個数を求めるには?