はじめに
みなさんこんばんは！！「さんすうがく」の赤い小人です。
本日も前回と同じく「 図形の移動と構成 」の図形を回転させる問題です。
前回間違えてしまった受験生は今度こそ正解させましょう！
今度こそ全問正解目指します！！
前回の問題はこちらから！！
↑ボタンをおすと問題ページにいきます。
図形が回転したとき、回転した角度はどこも同じ！
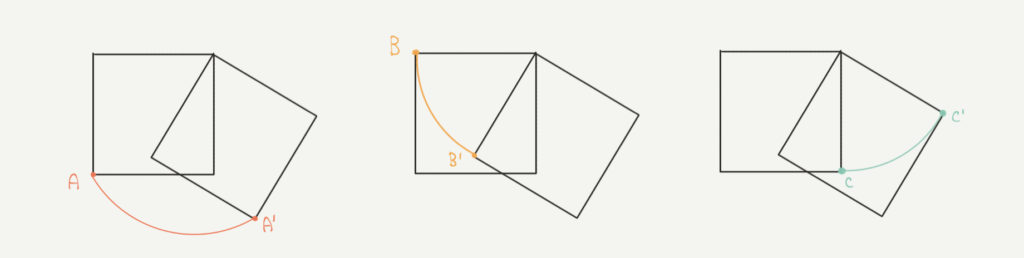
たとえば、正方形を回転させたとします。
このときAの点はA’へ、Bの点はB’へ、Cの点はC’へ移動しますよね？
図形をこのように回転させると、それぞれの点は円の弧の上を進むように動きます。
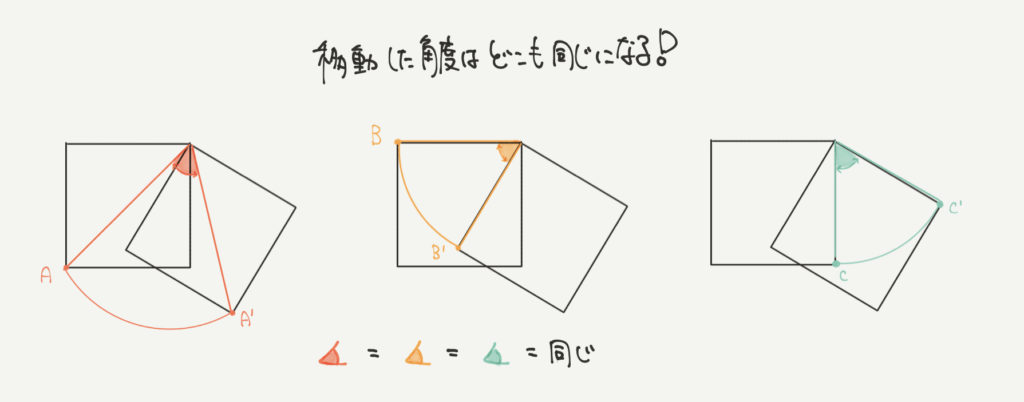
ポイントは回転させたときの角度がどこも同じになるということです。
同じ図形を回転させているので、それぞれの点A、B、Cが同じ角度だけ動くのは当然ですよね！
ですので、たとえばこの図形を60°の角度で回転させたとき、
角度＝角度＝角度＝60°となります！
今日はこのポイントを理解して問題に挑戦してみましょう。
「 図形の移動と構成 」の問題に挑戦！
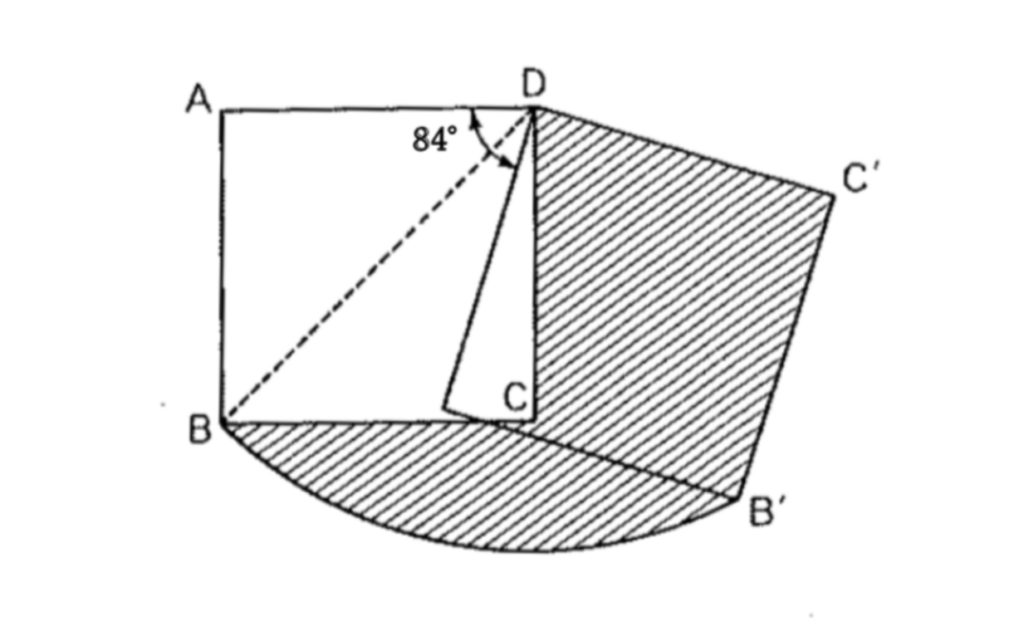
右の図のように、正方形ABCDを、点Dを中心として84度回転させました。正方形の面積を72㎠、また円周率を3.14として、次の問いに答えなさい。
① 角BDC’の大きさは何度ですか。
② 弧BB’の長さは何cmですか。
③ 斜線の部分の面積は何㎠ですか。
解答は次のページから！
- 1
- 2
