【中学受験算数を攻略】割合と比の問題を得意にする4つのポイントを徹底解説！

はじめに

中学受験では「和と差に関する問題」と同じくらい「割合と比」はよく出題されます。
和と差に関する問題を解く上でも「比」を使って解くやり方があったと思います。

この「割合や比」を苦手とする受験生のみなさんは百分率ひゃくぶんりつや歩合ぶあい、分数を小数にできなかったり、
何を基準きじゅんに比べればいいのかわからないといった方が多いんじゃないかと思います。

「割合と比」が苦手な受験生にこそ、この記事の説明を見ていただきたいです。
ていねいに説明していますので、一緒いっしょに勉強していきましょう！

この記事を書いている人はこんな人

割合と比で重要な解法

割合と比に関する問題の4つの重要なポイント

• 前項：後項、比の値
• 単位のそろえ方と考え方
• 逆比について
• 百分率、歩合、分数
  
  この記事では上の4つのポイントについて解説しています！

①前項：後項、比の値について

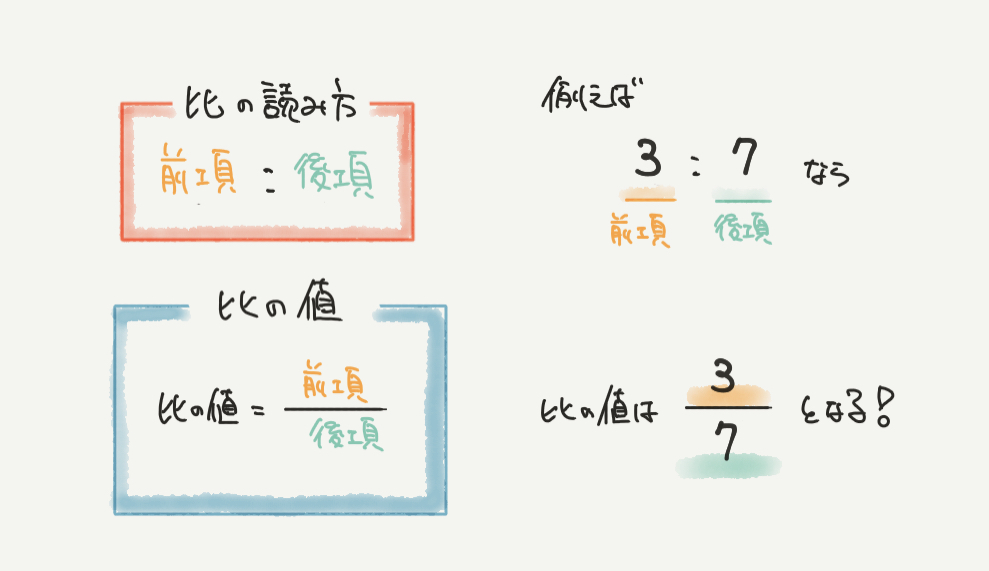
比の前項と後項という言葉は中学受験ではあまり出ないようなマニアックな問題です。

ただし、この「前項」「後項」「比の値」という言葉の意味を知らないと
問題を解くことができないのでかんたんに目を通して覚えておくようにしましょう。

②単位のそろえ方と考え方

問題を解くときは答えに単位を合わせると解きやすい！

次に単位について気をつけておいてほしいポイントを説明します。
受験生のケアレスミスで、最も大きな原因の1つは単位をごちゃごちゃにして計算してしまうことです。

たとえば、問題文で「〜何cmですか？」という問題が出てきたらなるべく「cm」の単位を計算するとやりやすいことが多いです。

割合の問題だけじゃなく、速さの問題とかでも単位がたくさん出てきます。
速さの問題では時速（○km/時）や分速（□m/分）など速さの単位がたくさん出てきますので、答えに合わせて単位をそろえるように注意しておきましょう！

単位はいちいち暗記する必要ない！

次に単位に関する考え方を説明しておきます。
単位をそろえるためには単位に関する知識を勉強しておかなければいけません。

覚えなくてもわかる単位の思い出し方を面積の単位aとhaを使って紹介しょうかいしていきます。

aとhaの思い出し方

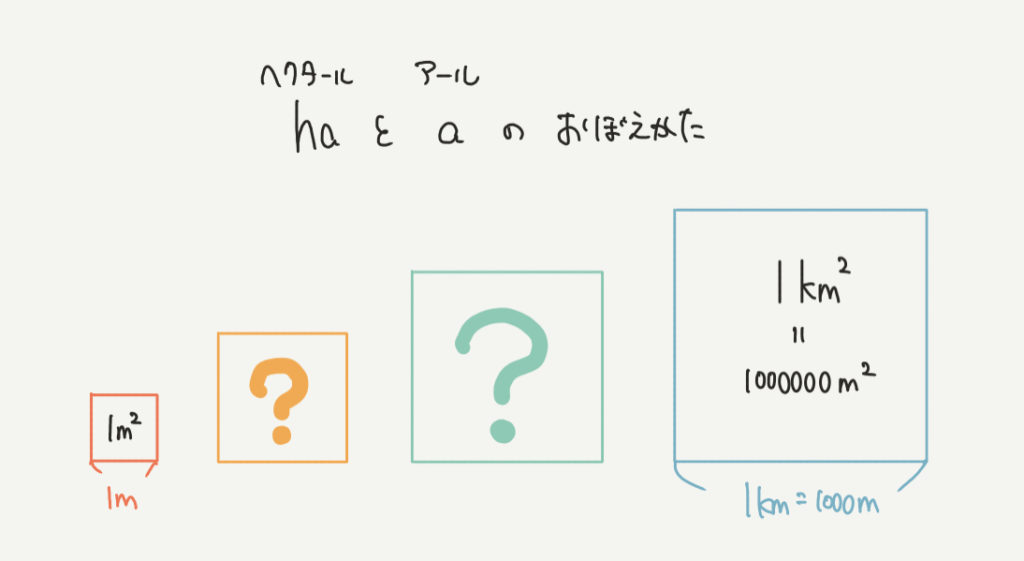
たとえばこちらの記事では、受験ではあまりでないけど知らないとわからない「a」と「ha」について解説していきます。

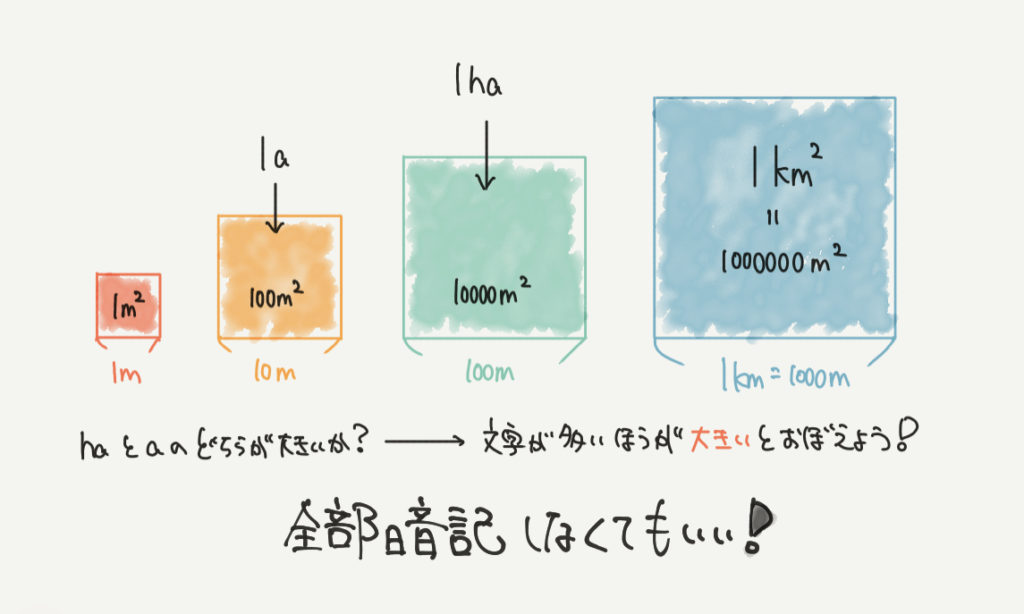
「a」と「ha」であれば、上のように1㎡と1㎢の単位さえわかっていれば、
その間の大きさがaとhaと勉強するだけで思い出せると思います。

あとは「ha」の方が「a」大きいとさえ覚えておけば、
いちいちa＝100㎡、ha＝10000㎡と暗記しなくても大丈夫だいじょうぶです。

今のはほんのひとつの例ですが、他にも「覚えないといけない単位」と「覚えなくてもなんとかなる単位」があります。

公式にも覚えないといけない公式と覚えなくてもいい公式がある

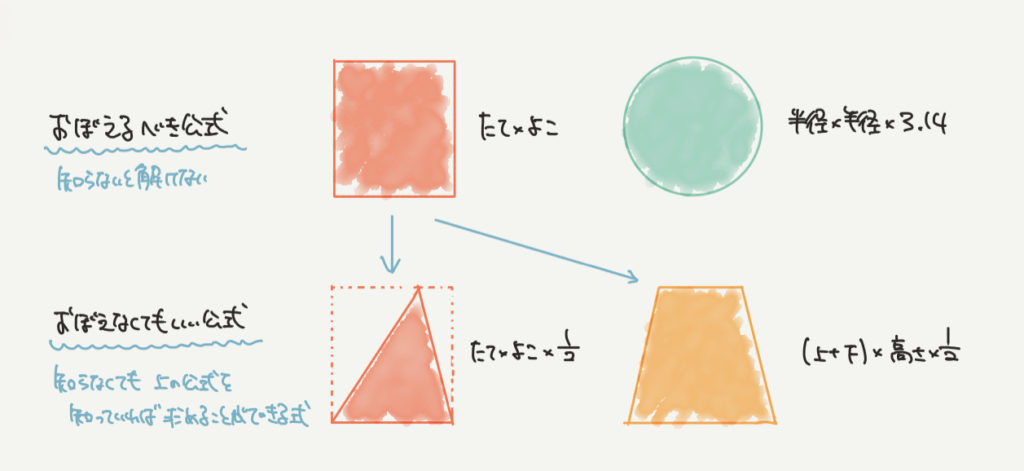
公式なども同じで、絶対に覚えないといけないものだけ効率よく覚えていきましょう。

たとえば四角形の面積や円の面積は暗記してもいいと思いますが、
三角形の公式や台形の公式は四角形の公式さえ分かっていれば暗記しなくても覚えることができますね。

③逆比について

速さの中にある逆比

次にここでは逆比について勉強したと思います。

まずは速さの問題で出てくる逆比についてです！
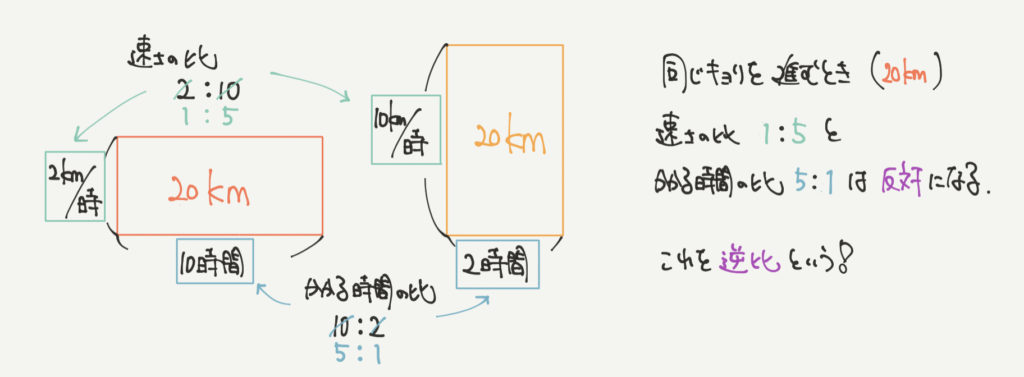
この面積図では20kmを2人が走った場合を考えましょう。

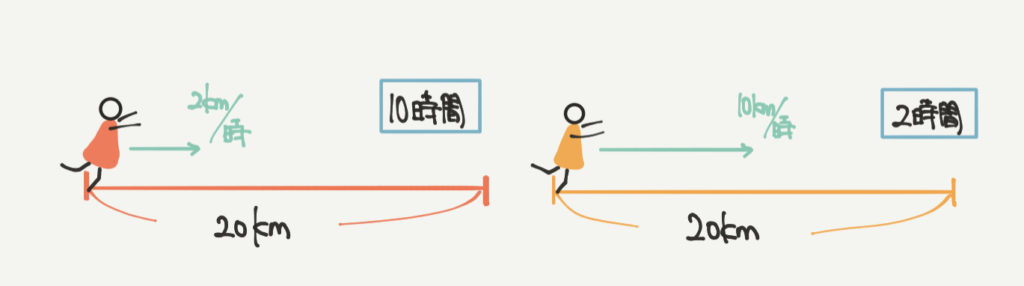
赤い小人は時速2kmで20km進みますので、
20km÷2km/時＝10時間かかります。

一方で、黄色い小人は時速10kmで20km進みますので、
20km÷10km/時＝2時間かかります。

このとき赤い小人と黄色い小人の時速の比は
2km/時:10km/時＝1:5となります。

そして20km進む時間の比は反対の5:1になりますね。
このように比が反対になることを逆比と言います。

歯車の中にも逆比はある

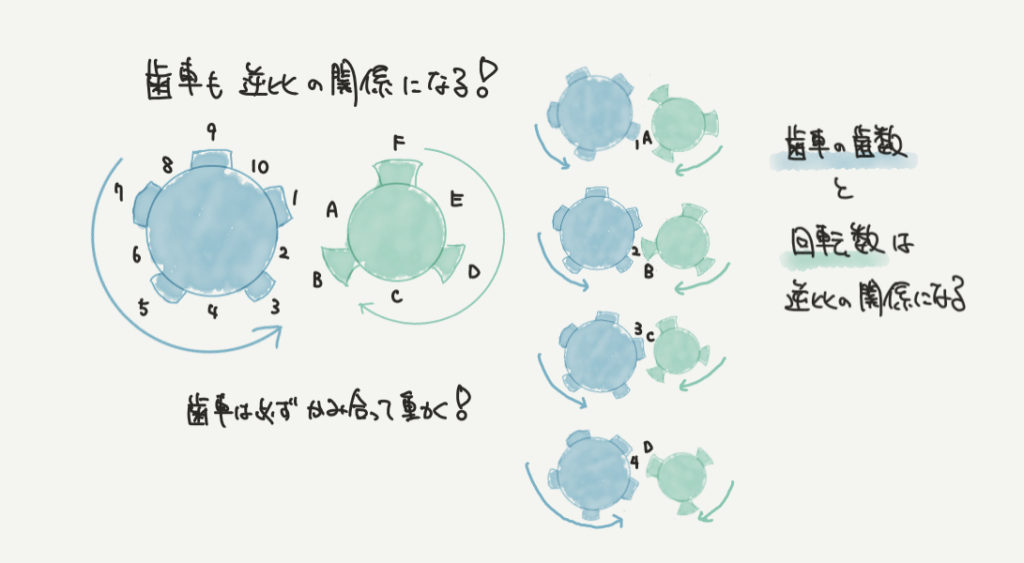
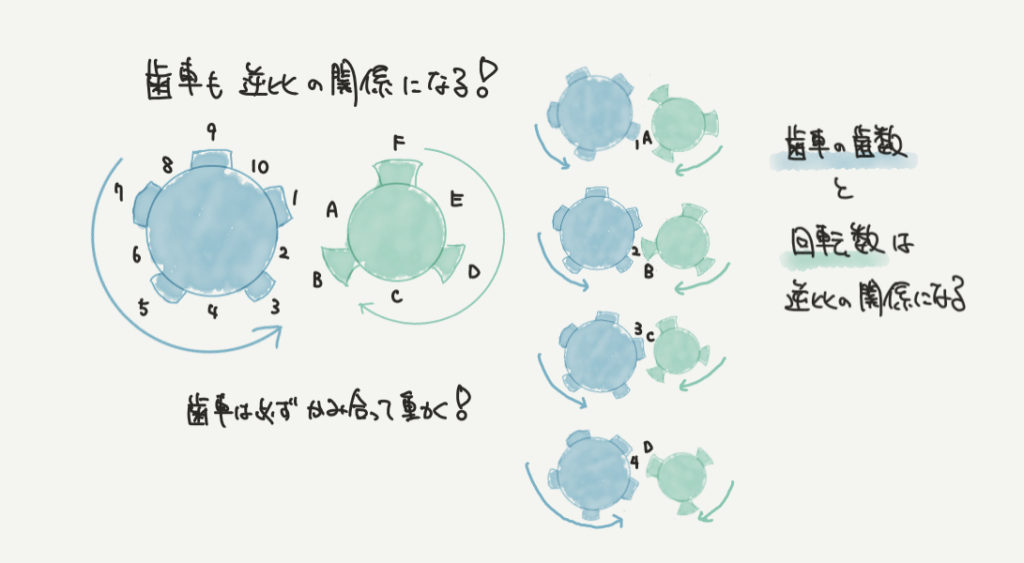
次に歯車を使って、逆比について説明していきます。
大事になってくるのは歯車が必ず噛かみ合って動くという点です。
そのため、1とAは対応して、2とBも対応してというふうにそれぞれは噛かみ合いながら歯車は動いていきます。

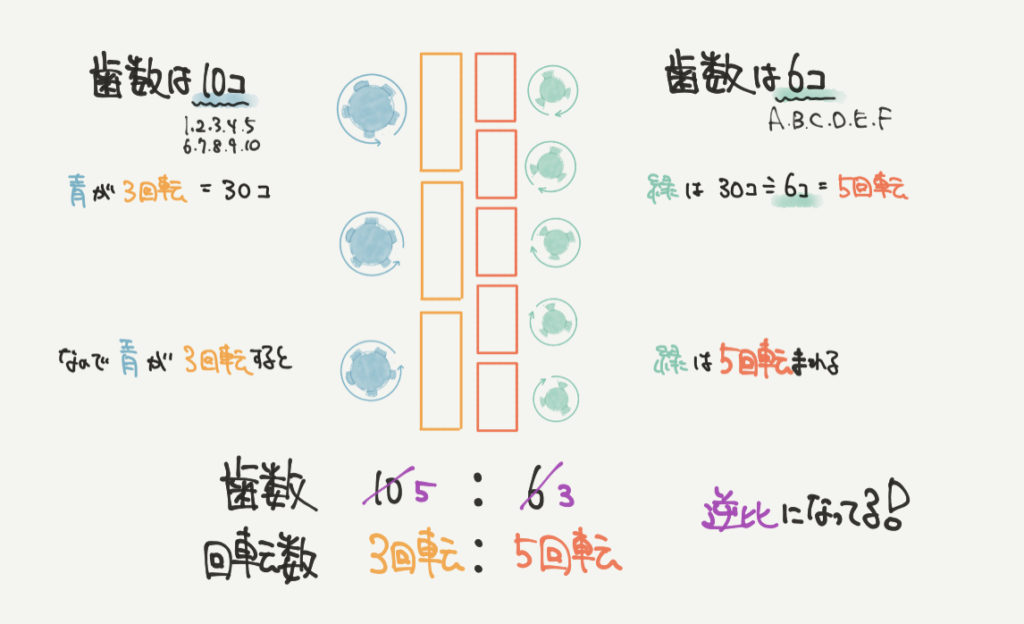
すると、歯数10の歯車が3回転するとちょうど歯数6の歯車が5回転することがわかると思います。

歯数で考えると、
青の歯車は3回転で10コ×3回転＝30歯数分進む
緑の歯車は30歯数分進むので、30歯数÷6コ＝5回転

こちらは歯車の歯数の比（10:6=5:3）と回転する比（3:5）が反対になっています。
これも逆比の考え方になります。

④百分率ひゃくぶんりつ、歩合ぶあい、分数

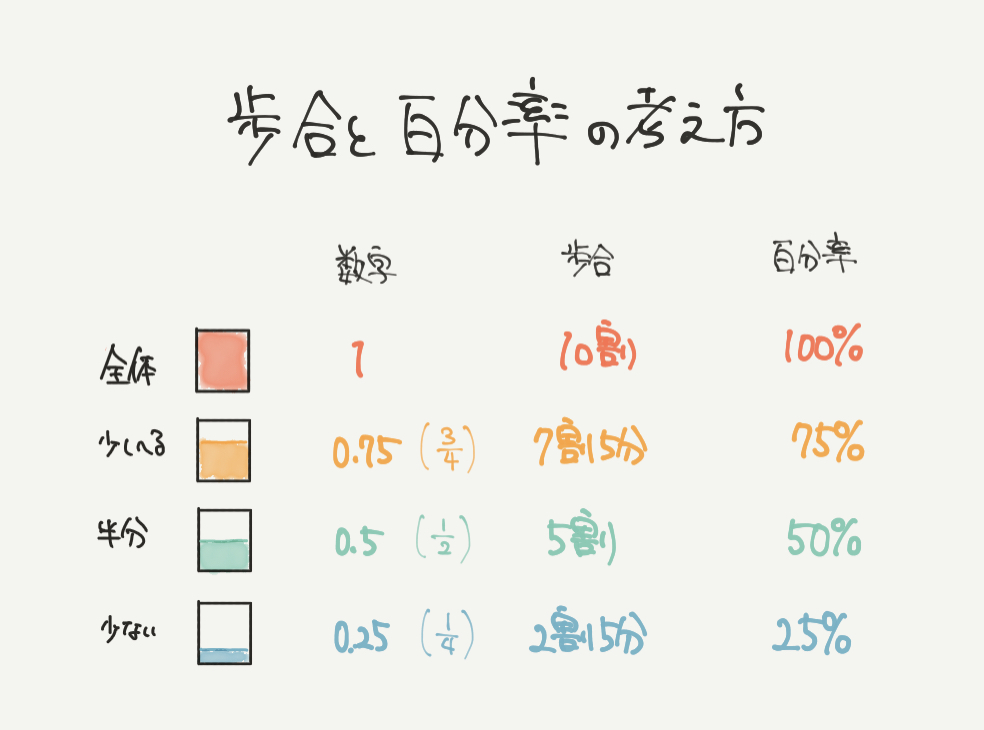
最後に割合を表すために用いられる方法を3つ解説します。

百分率：全体を100％として割合を表している。つまり100％が最大です。
歩合：全体を10割として比べている。なので10割が最大になります。
分数：全体を1として比べている。

つまり、100％＝10割＝1ということです。
基本的に「％」は食塩水などの問題で使われ、「割」は売買損益で使われます。

やってはいけない計算方法

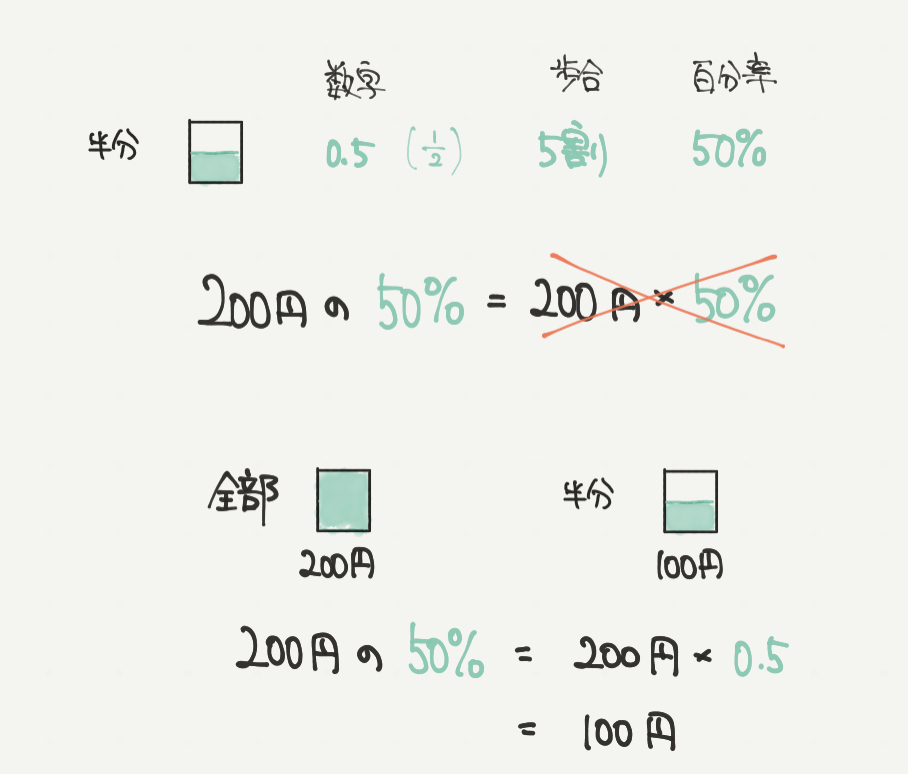
ここで注意してほしいのは「％」と「割」の数字で計算してはいけないということです。

たとえば、200円の50％はいくつか？という問題では、
200円×50%=10000円としてはいけません！！

「％」や「割」は割合を表しているだけなので、実際の計算では「分数」を使って解くようにしましょう。

割合と比の問題を得意にする4つのポイントのまとめ

割合と比の問題の4つの重要なポイント（復習）

• 前項：後項、比の値
• 単位のそろえ方と考え方
• 逆比について
• 百分率、歩合、分数

この内容だけ見ても頭は良くなりません。
ちゃんと上の4つのポイントを意識しながら問題に挑戦ちょうせんしていくことが大切です。

「割合と比の問題」ですが以上の4つの点を勉強してから問題に挑戦ちょうせんすれば今までよりもかんたんに問題を解くことができると思います。
「％」や「割」など、割合の表し方がいくつかあるのがめんどくさいですよね。

ですが、売買損益や食塩水は今後も必ず出てきますし、それらの問題で割合の考え方は必ず使います。
それだけでなく、「割合と比」は他の単元とも関係しているので「割合と比」を得意に変えられると算数の点数は大きく変わりますよ！

これを読むだけですと、勉強した気になっているだけになってしまいますので、実際じっさいに問題を解いてたくさん経験を積んでいきましょう！