はじめに
みなさんこんばんは!!「さんすうがく」の赤い小人です。
「 図形の移動と構成 」の単元の問題もいったんこれでおしまいです。
今まで習ったことを活かして問題にチャレンジしていきましょう〜
図形の移動の問題は「直角三角形」「正三角形」に続いて3問目ですね!
はい!先にこれまでの問題を解いておきたい受験生はこちらから問題を解いてみてくださいね。
直角三角形を回転させる問題はこちらから!

正方形を回転させる問題はこちらから!

おうぎ形の回転はどんな形?
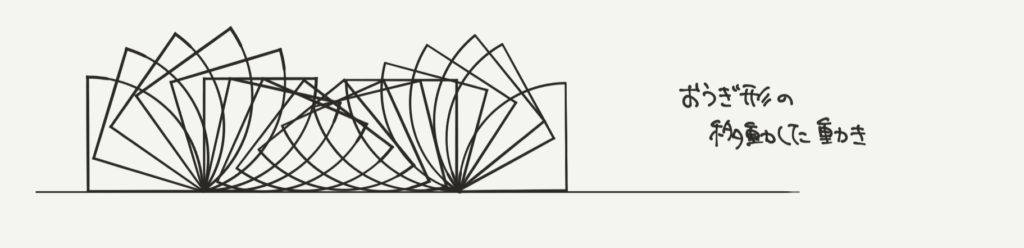
今回の問題ではおうぎ形の回転の問題が出てきます。
おうぎ形が回転する時のイメージはこんな感じです↑
少しみづらいかもしれませんが受験生のみなさんが、想像しやすいようにかなり細かく書いてみました。
これでおうぎ形がどのように移動するのかなんとなくイメージがついてきたと思います。
それではここからおうぎ形の点がどのように移動するのか見てみましょう!
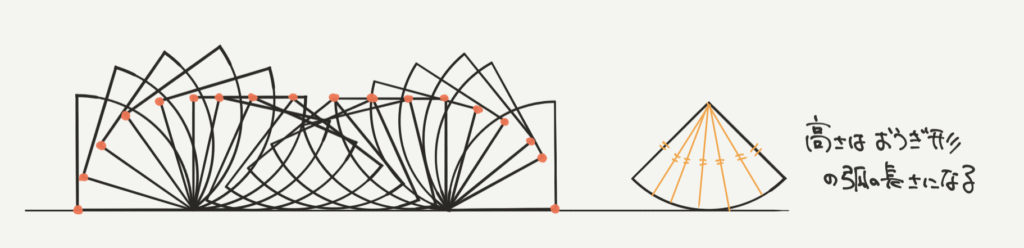
今回はおうぎ形の赤い点の移動線についてみてみましょう。
赤い点は途中まで円の弧のように動いていきますが、その後一直線になります。
そしてまた最後に円の弧のようにゴールに移動します。
ポイントになるのが一直線です。
おうぎ形の移動した線がなんで直線になるのかわからないです。
それはおうぎ形の頂点から弧までの長さがどれも同じだからです。(右図)
なので、どのようにおうぎ形が回転しても頂点までの長さは必ず半径の長さと同じになります。
つまり・・・!
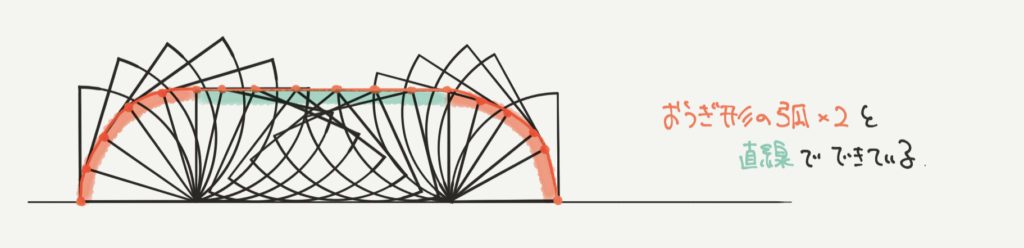
おうぎ形が移動した時の線を「部分と部分に分けて考える」とおうぎ形の弧×2と直線でできていることがわかります。
今回の問題ではこのおうぎ形の移動の知識を使って解いていきましょう!!
「 図形の移動と構成 」の問題に挑戦!
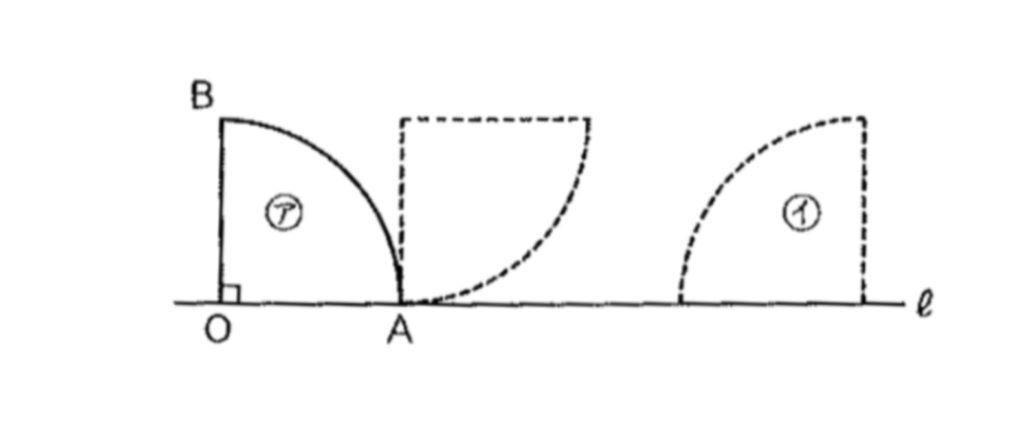
半径6cmの四分円OABを、右の図のアの位置から、直線ℓに沿って、初めてOBが直線ℓ上にくるイの位置まですべることなくころがしました。円周率を3.14として、次の問いに答えなさい。
① 点Oが動いたあとの線を、図にかき入れなさい。
② 点Oが動いたあとの線の長さは何cmですか。
③ 点Oが動いたあとの線と、直線ℓとで囲まれる部分の面積は何㎠ですか。
解答は次のページから!