【中学受験算数】「割合と比」を攻略！AとBの比、BとCの比から、AとBとCの比を求めてみよう！（３連比）

はじめに

みなさん、こんにちは！
今日は天気が悪かったですね〜。近くですごい大きな雷かみなりも聞こえました。
天気が悪いとやる気も下がってしまうので、早く晴れになってほしいですね〜☀️

今日解く問題は「割合と比」です！！
今回の記事では三連比さんれんぴとよばれる考え方が出てきます！

↑三連比さんれんぴとは？２つの比を合わせて、３つの比を出す考え方のことです。

例えば、赤い小人、黄色い小人、緑の小人がそれぞれ10円、50円、500円を持っていたとします。

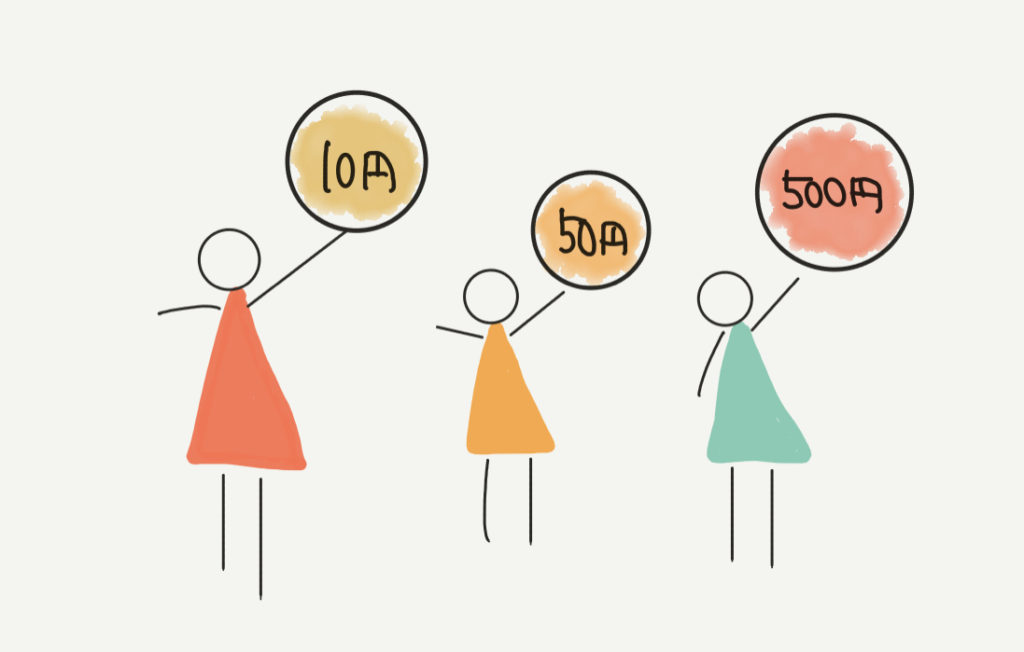
赤い小人をA、黄色い小人をB、緑の小人をCとすると、3人の金額きんがくの比は下のようになります。

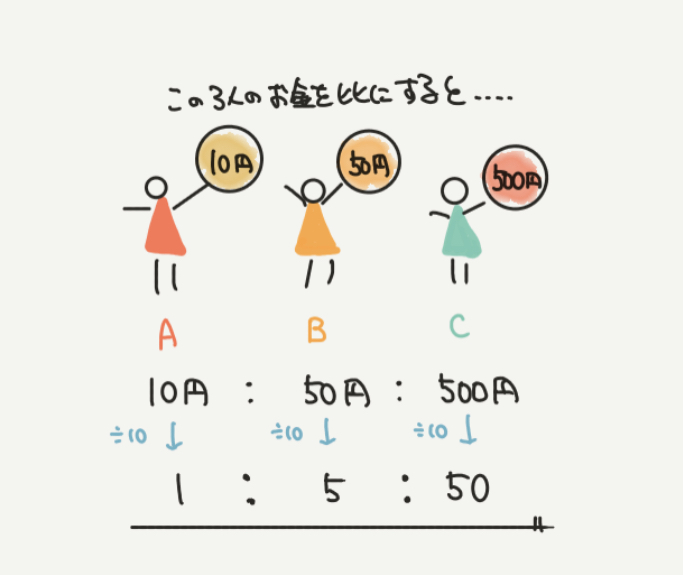
三連比さんれんぴの問題は、3人のお金がわからないときでも求もとめることができます。
下のようにA：BやA：Cなどのある比が２つわかっていれば答えを出すことができるんです！

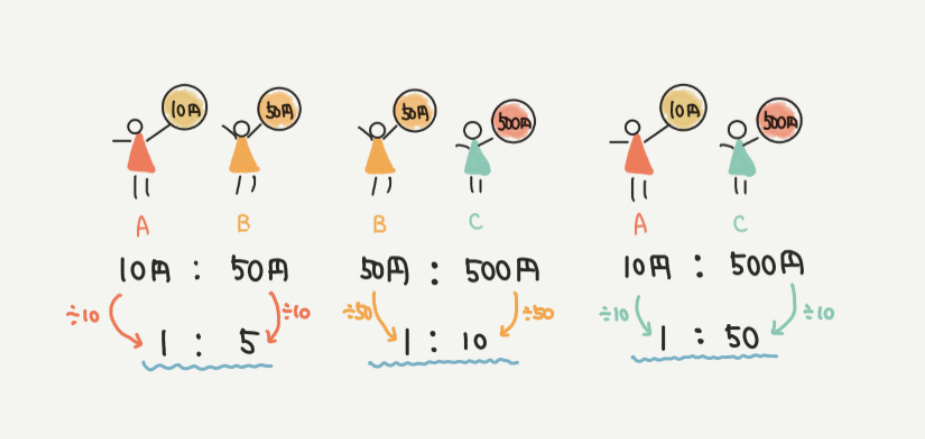
A：B＝1：5
B：C＝1：10
A：C＝1：50
になりますね。

ではこれらの比から、３つの比を○：□：△と答えるにはどうしたらいいのでしょうか？
（今回ならA：B＝1：5、B：C＝1：10からA：B：C＝1：5：50と求もとめていますね！）

それではさっそく問題に挑戦ちょうせんしていきましょう！

〈プロ講師のみ〉数学が苦手な生徒のための個別塾「数強塾」

問題に挑戦ちょうせん！

長さ84cmのひもをA、B、Cの３人で分けたところ、AとBの長さの比が3：4、AとCの長さの比が6：7になりました。
Bのひもの長さは何cmですか。

解答

この記事を書いている人はこんな人

解説を読んで「 割合と比 」を攻略こうりゃくしよう！

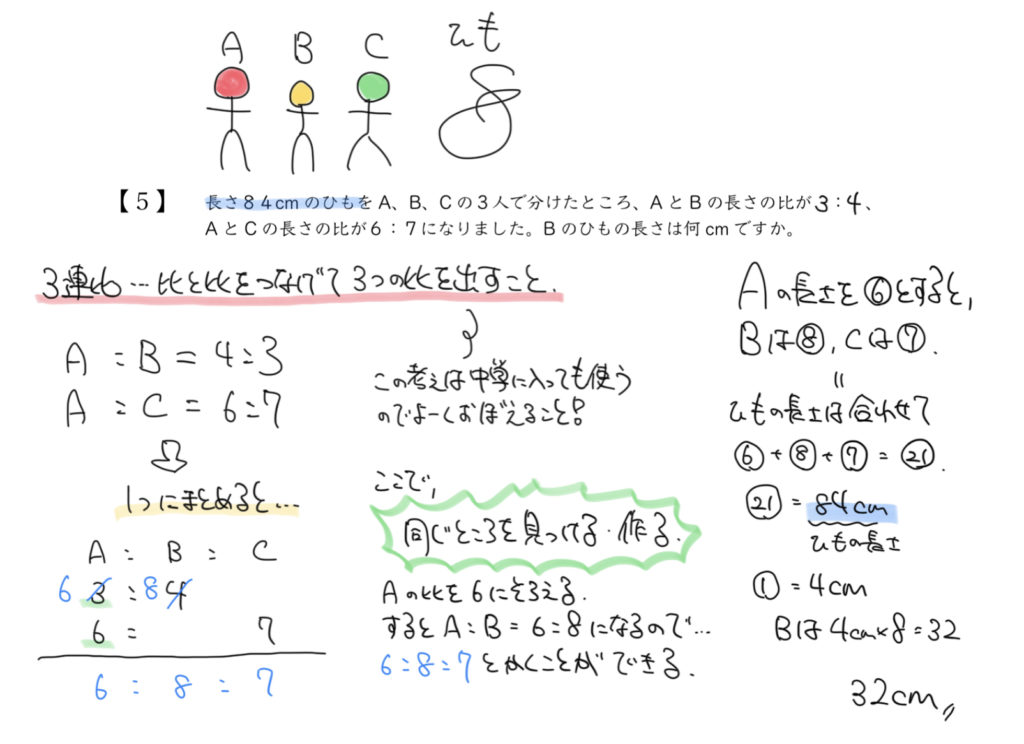
STEP1：3人の比を求もとめるために注目するところ

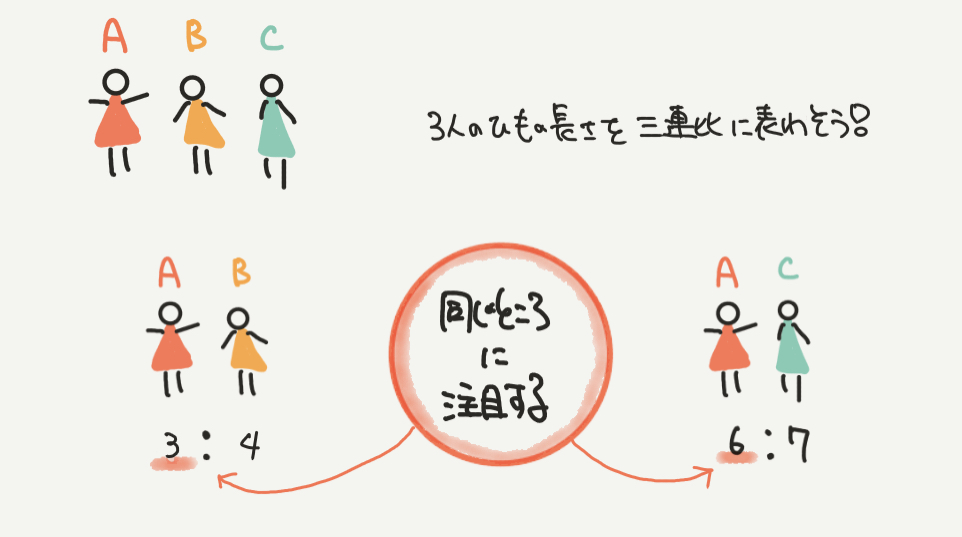
この問題のポイントは２つの比を合わせて作る、三連比さんれんぴです！
A：B＝3：4とA：C＝6：7なので
同じ部分であるAの比を基準きじゅんに3人の比を出しましょう！
（今回はAがどちらも比で表されています）

STEP2：どこの数字をそろえる？

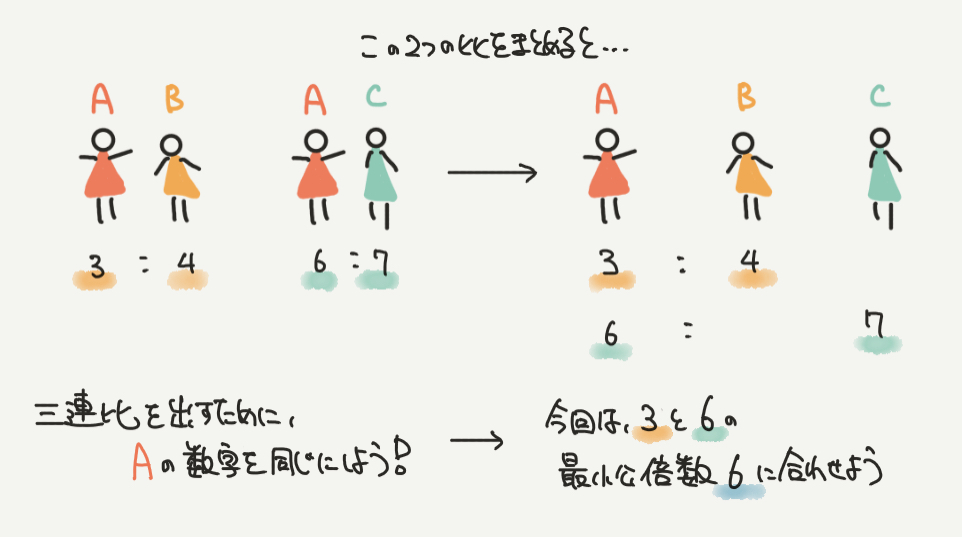
さあ、ここから3人の比を出していきましょう。
A：B＝3：4と、A：C＝6：7のAに注目して、数をそろえていきましょう。
今回は3と6の最小公倍数の6に合わせると、3つの比をカンタンに出すことができます。

STEP3：三連比さんれんぴを求めよう！

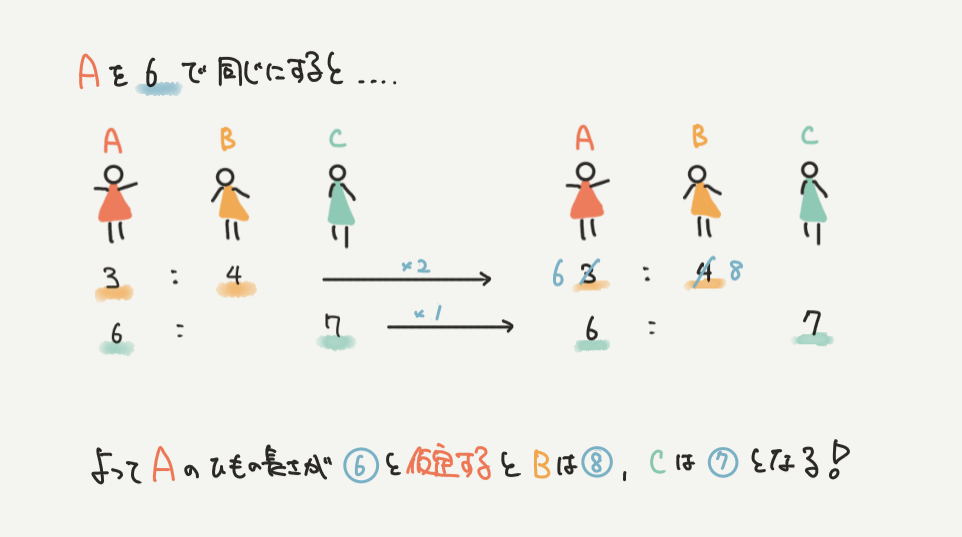
Aを6でそろえて、比を書き直してみましょう。

A：B＝3：4なので、
A：B＝6：8になりますね！

A：C＝6：7なので、これでAの数字を６にそろえることができましたね！

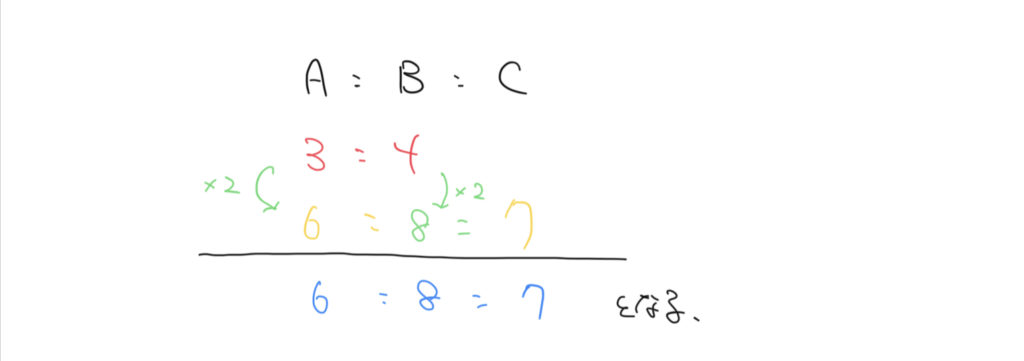
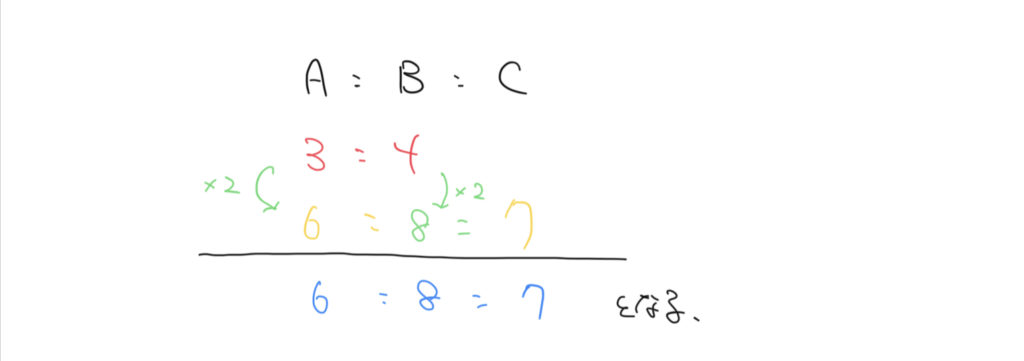
よって3人の比をA：B：C＝6：8：7となり３つの比を求めることができます。

STEP4：あとは仮定して計算していこう！

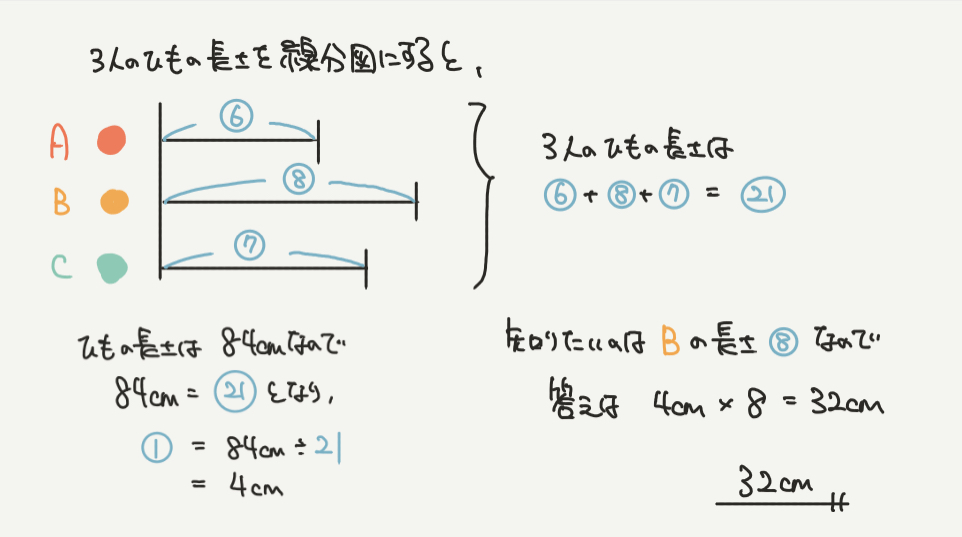
最後は仮定の考えを使っていきましょう。
STEP3でAのひもの長さを⑥とすると、Bは⑧、Cは⑦と表すことができましたね。

この3人のひもの長さを足すと84cmになると問題文に書いてあるので、
⑥＋⑧＋⑦＝㉑になり、この㉑＝84cmになります。
よって①＝4cmと求もとめることができます。

今回はBの長さを知りたいので⑧を計算すればいいことになります。
よって、4cm（①）×8＝32cmと計算できました！

３つの比を出して、ひもの長さを求める問題のまとめ

今回の問題で大事なポイント

同じところを見つける、作る（STEP1）
三連比さんれんぴの考え方（STEP2）
仮定する考え方（STEP3）
・もし○○が□□だったら〜と考えてみましょう！

おつかれさまでした！
これが三連比さんれんぴの問題でした。いかがでしたでしょうか？
なるべくわかりやすく、ていねいに解説しましたがわからないことがあれば遠慮えんりょなくコメントで教えてくださいね！

三連比さんれんぴはまた必ず出てくるキーワードです！
この三連比さんれんぴの考えは中学受験はもちろん、高校受験の平面図形でもたくさんに出ますので、今のうちからよく復習しておきましょう！！

お子様をほったらかしにしない仕組みも充実【ネット松陰塾】

【学力も成績もグン！と引き上げる東京個別指導学院】

その他の単元の問題の復習はこちらから！