はじめに
今回も平均算の問題に取り組んでいきましょう。
平均点の問題はさんすうがくではこれで3回目になります。
この記事を見るだけで理解できるように書いてありますのでぜひ一緒にがんばっていきましょう!
もうすでに問題解いているから大丈夫!という受験生はさっそく問題に挑戦してみましょう!
平均の考え方の復習
はじめて問題を解く受験生のためにも、まず復習からしてみましょう。
平均とは超かんたんに言うと「だいたいこれくらいの数字」のことでした。
たとえば、クラスにいる5人の小人(赤、黄、緑、青、紫)がテストを受けたとします。
それぞれの点数は90点、10点、70点、40点、50点とかなりバラバラです。
このとき、みんなのテストの平均点(みんながとっただいたいの点数)はどのように求めればいいでしょうか。
はい。
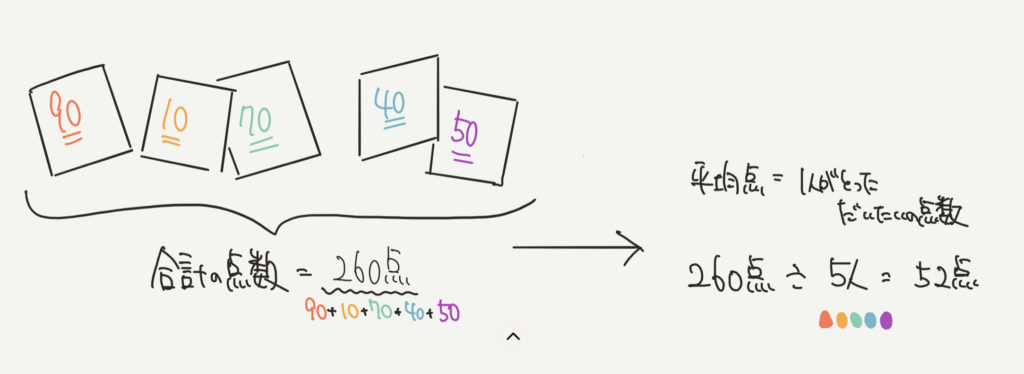
平均点は、全員が取った点数÷人数=1人あたりがとった点数(1人がとっただいたいの点数=平均点)となります。
ですので、
90点+10点+70点+40点+50点=260点となります。
5人で260点をとっているので、1人がとった平均点は、
260点÷5人=52点/1人と求めることができました。
 わかみや先生
わかみや先生このような形で平均について勉強しましたね。
問題に挑戦!
解答
答えを見るにはここをクリック!
3:5(A組:B組)
この記事を書いている人はこんな人


解説を見てみよう!
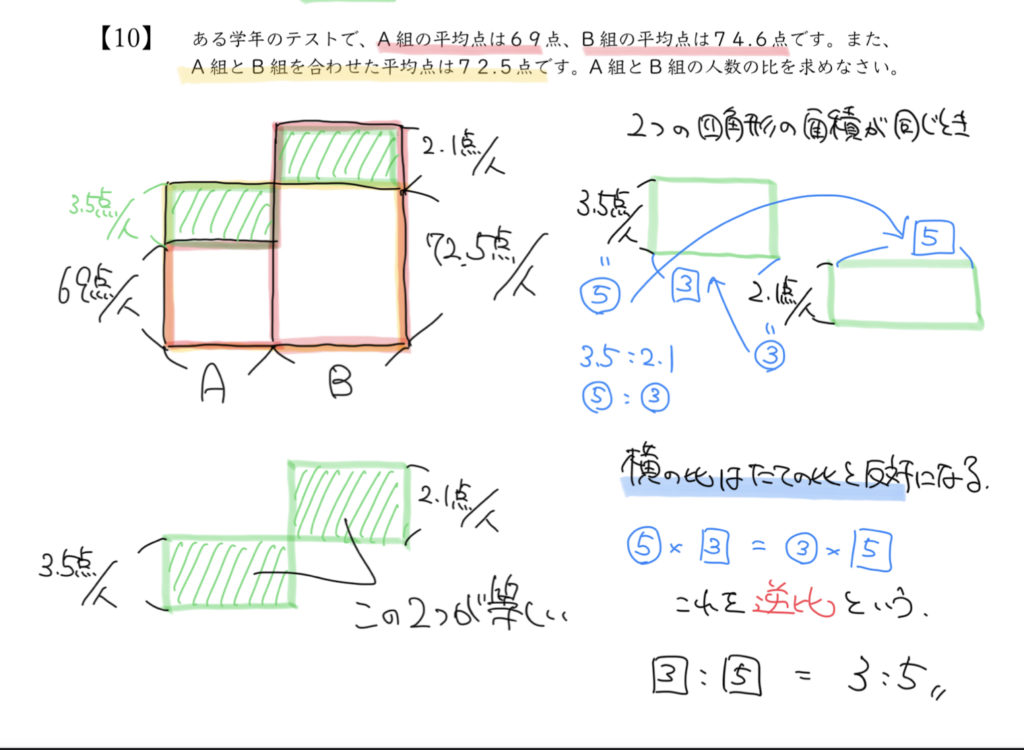

平均点の問題のときは面積図を書くとわかりやすかったですね。
まずは解説のように面積図を書く練習をしてみましょう。
左の赤の面積図のようにA組の合計点数(Aの人数×Aの平均点)と
B組の合計点数(Bの人数×Bの平均点)を書いてみましょう。
それぞれのクラスの平均点とA組とB組の合計の点数、平均点を黄色の四角形にしていくと、
緑の四角形の面積が同じであることに気がつけると思います。



下の図は解説と対応している色がちがうので気をつけてくださいね!
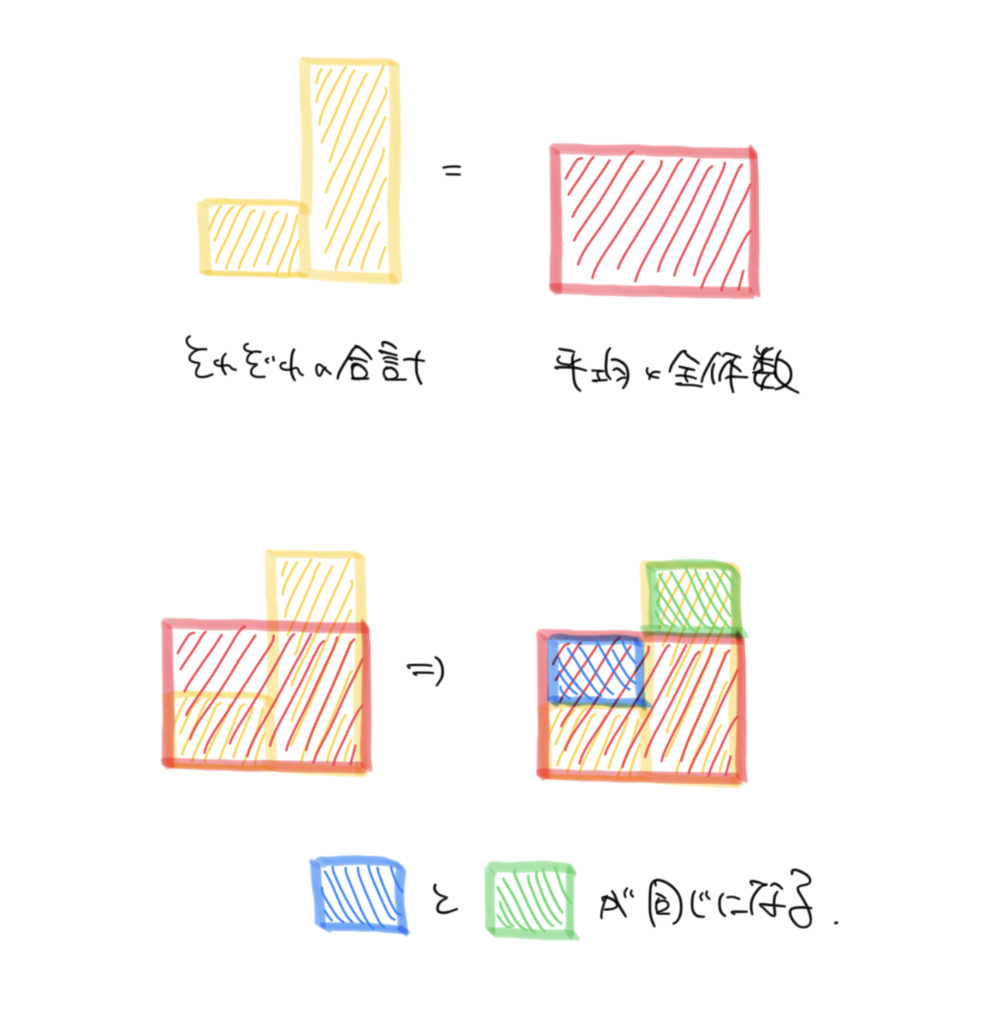

この2つの四角形(緑色)の面積が同じなのであとは計算して求めればいいのですが、
ここで問題が発生してしまいます。
A組、B組の人数が全くわからない!!
でも安心してください。
A組、B組の人数がわからなくても、大丈夫です。
なぜなら、今回求めたいのはA組とB組の人数の比なので
具体的な数字が分からなくても問題を解くことができます。
かんたんに説明すると、面積が同じ2つの四角形があるとき、
たての長さの比と横の長さの比は反対になります。(分からなくても大丈夫!今から説明します。)
たとえば、面積が15の四角形があるとします。(赤と黄)
赤の四角形と黄色の四角形のたての長さの比が3:5のとき、
横の長さの比はその反対である5:3になります。
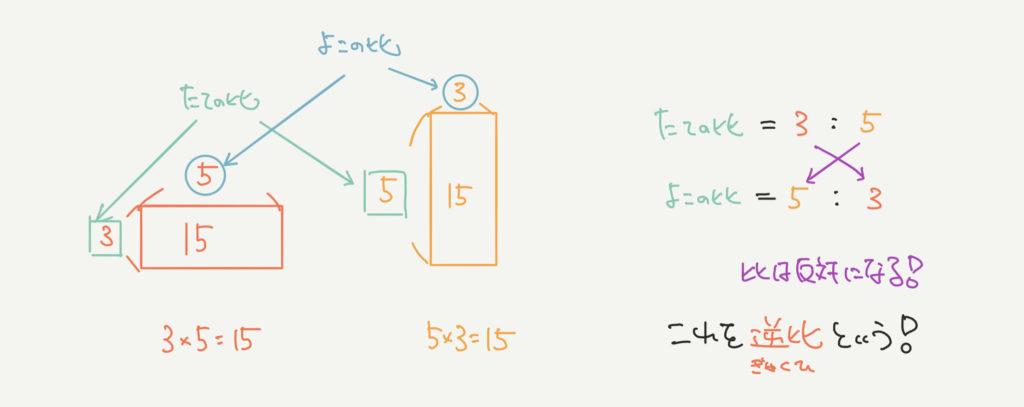

今回の緑の四角形のたての比は3.5:2.1ですので比にすると5:3となります。
(2つの数字を0.7で割ると比を求めることができます。)



比は最もかんたんな整数で表すので、小数の数字を直しましょう!
2つの四角形の面積が同じとき、横の比はたての比と反対になるので
A組とB組の比(四角形の横の長さの比)は3:5となります。
算数を得意にするコツ
この問題では逆比という考え方が出てきました。
逆比とは、2つの四角形の面積が同じとき、たての比と横の比が反対になる、
といったよう比に関する考えのことです。
この逆比の考え方は今後、多くの問題で使われる解法なのでよく練習しておきましょう。
こまったら、イラスト解説のようにかんたんに四角形を書いてみて自分で確認するようにしてみましょう。
実は逆比の考えがわかっていたらすぐに解けたという問題がすでにあります!
クラスの平均点からクラスの人数の比を求める問題のまとめ
今回の問題で大事なポイント
平均の考え方(だいたいこれくらいの数のこと)
・平均算のときの面積図の書き方
・同じところを見つける、作る
逆比の考え方
さて、平均の問題はいかがでしたか?
今までの問題を解いてくれた受験生なら気づくと思いますが、
面積図を書く、同じところを見つけるだけでは解けないむずかしい問題でしたね。
この問題で特に大事だったのは、逆比の考え方を理解することでした。
逆比は面積図など、四角形の面積が出てくる問題に使うことができます。
さんすうがくではほかにも面積図を使う問題がたくさん出てきますので、
逆比を使って解いてみるとより実力が身に付きますよ!