はじめに
まだまだ和差算の問題は続きます。今回の問題は線分図を書いて解くのとは違い、
単位量あたりの数字というものが出てきます。
算数が苦手な受験生はここで困ってしまうかもしれません。
ですが、諦めないでください!僕もはじめはチンプンカンプンでした!
そもそも単位量あたりというのはどういうことなのか?
単位量あたりの数とは、ある単位につき○○(数字)といったものの量を表す時に使われます。
例えば、
- 1時間500円(1時間につき、500円のお金がかかる)
- 時速60km(1時間で60km走ることができる)
- 1匹あたり4本の足(1匹に足が4本ある、つるかめ算の問題で出てきますね)
- 1人に2個ずつ(2個/人とも人ともかくことができます)
- 平均点が59点(1人あたりの点数が59点)
などなどのことを単位量あたりの数と受験では呼びます。
これをふまえての例題にチャレンジしましょう。
例題に挑戦!
 わかみや先生
わかみや先生さあ、考えてみましょう!!
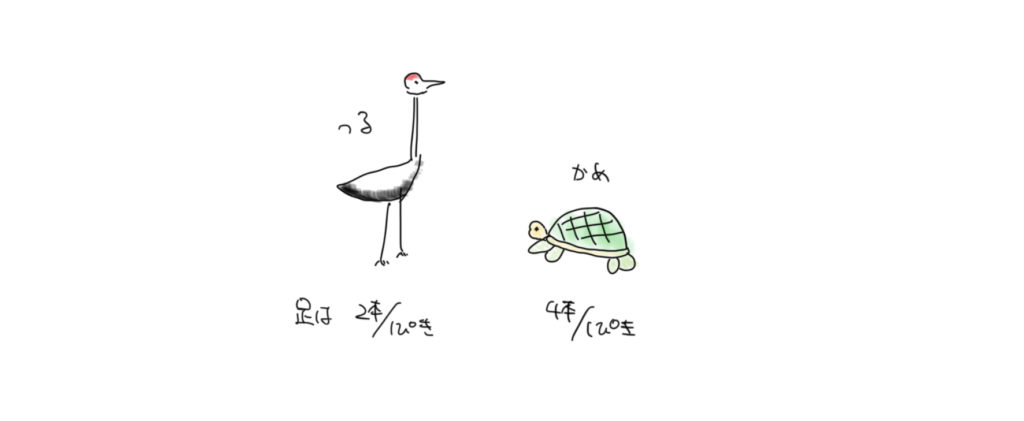

解答
つる1匹、カメ9匹です!!
解説を見てみよう!
解き方には面積図を用います。それでは解いていきましょう。
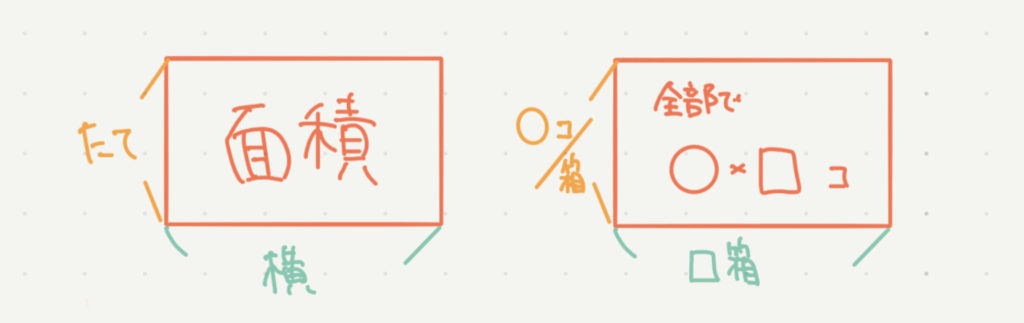
面積図の書き方はとても簡単です!
たてに足の数、横に動物の数、足の本数を面積として書いていきます。
このように図を書くことで、
足の数(たて)×動物の数(横)=全部の動物の足の数の合計(面積)
と考えることができます。これが面積図を書くことが便利な理由です。
さあ、まずは問題文の内容を図にしてみましょう。
黄色の四角形がつる、赤い四角形がカメの足の合計の数になります。
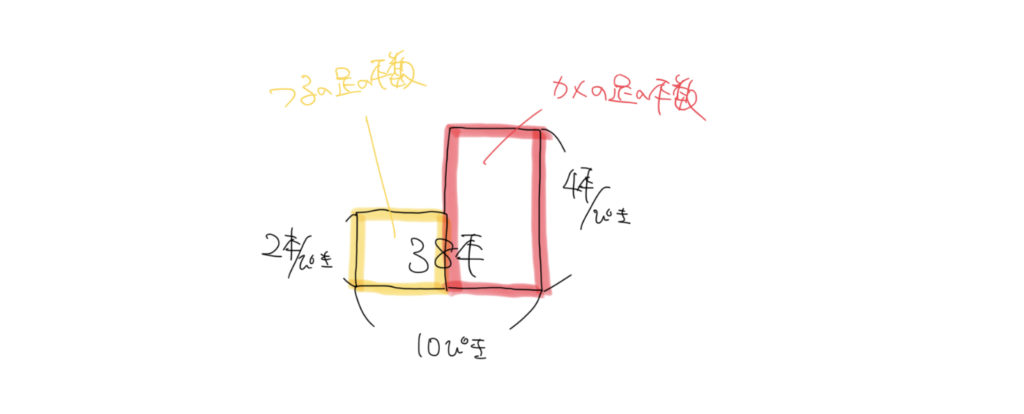




ここまで書けましたか?
そうしたらここからもう1ステップです。この黄色と、赤い四角形に青い補助線を引いてみましょう。
さっきの黄色と赤い四角形の図に青い補助線を引くと、大きな四角形(青)ができると思います。
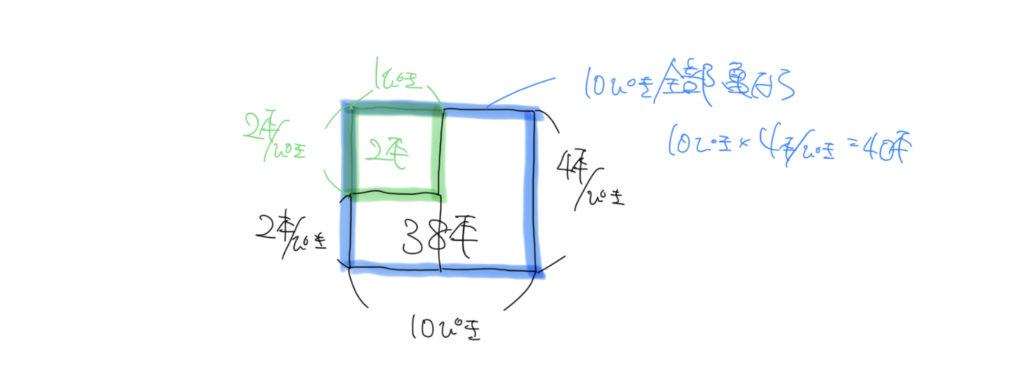

この大きな青い四角形は横の長さが10匹で、たての長さが4本/ひきになっているのがわかると思います。
つまりこの青い四角形は、
横×たて=青い四角形の面積
10ひき×4本/ひき=40本
(10ひきがカメだった時の足の数の合計になります。)
しかし実際には38本なので、
大きな青い四角形から赤い四角形+黄色の四角形を引くと、
青い四角形(40本)–(赤い四角形+黄色の四角形(38本))=緑の四角形(2本)となり、
2本分の面積が緑の四角形と求めることができます。
この緑の四角形の高さは4本/ひき−2本/ひき=2本/ひきとなり、
2本(緑の四角形)÷たて(2本/ひき)=1ひき
つるが1ひきであると求めることができます。
よってカメは10ひき−1ひき=9ひきとなります。
このような面積図をつかったやり方もさんすうがくでは頻繁に使用しますし、
何より解きやすいのでぜひ書き方を覚えるようにしてください!!
それでは問題です!
問題に挑戦!
解答
答えを見るにはここをクリック!
12箱
この記事を書いている人はこんな人


解説を見てみよう!
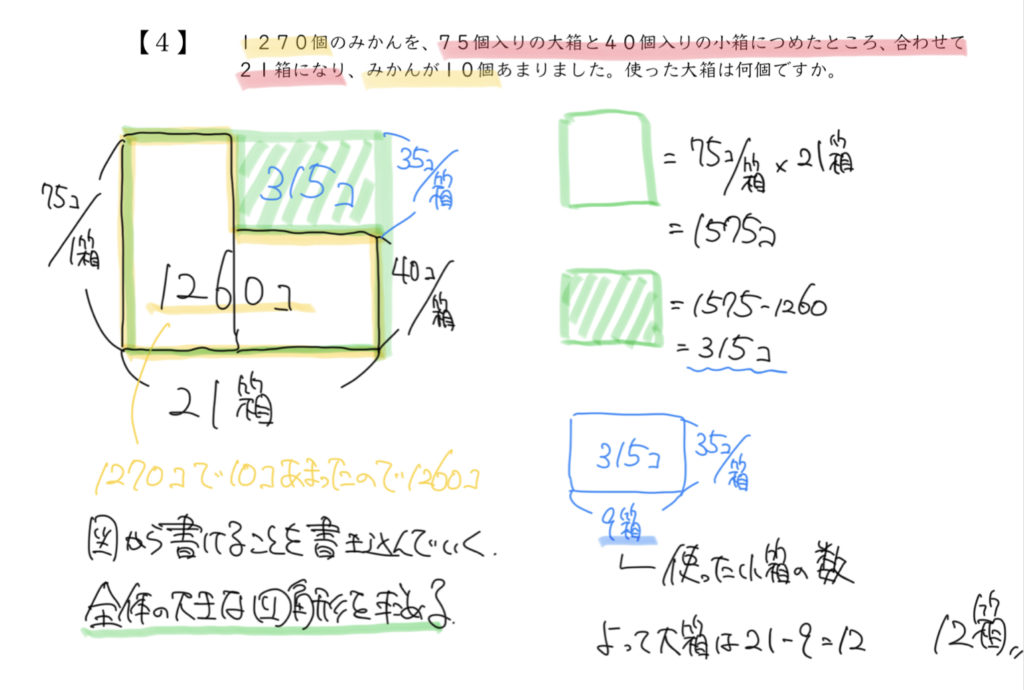

今回の問題も単位量あたりの数(1箱75個と1箱40個)が使われているので面積図を書くとわかりやすいと思います。
例題でもお話ししましたが、面積図で書くと良い点は簡単にたて×横の計算ができることにあります。

解説の面積図は問題文に沿って書かれたものです。
この図をまずはきちんと書けたかどうか、確認しましょう。
そして面積図が書けた受験生はこの問題から追加でわかることを探してみましょう。
今回追加でわかる情報は、もし21箱全てが、75個入りの大箱だった場合何個のみかんを入れられるかという情報を求めることができます。
この数が緑の大きな四角形の面積が、もし21箱全てが、75個入りの大箱だった場合のみかんの数になっています。
例題にも書いてありましたが、
①面積図を書く
②補助線を引いてわかる面積を増やしていく、書ける情報を増やしていく
というのが一般的な解法、解き方になります。
全て大箱だとみかんは21箱×75個/箱=1575個入れることができますが、
実際にあるみかんは1260個なので、
1575個−1260個=315個が小さい緑の四角形の面積となります。
そして小さい緑の四角形の面積が315個と分かれば、あとはたての長さ35個/箱で割ればいいので、
315個÷35個/箱=9箱と求めることができます。
ただしこの9箱は大箱ではなくて、小箱の数なので注意してください!
求めたい大箱の数は箱の合計21個から小箱9個を引いた12個と求められます。
算数を得意にするコツ
まずは問題を読んでしっかり面積図を書く練習をしてみましょう。
どんなに簡単な問題でも、図をしっかり書いて練習するようにしましょう。
そこから大事なのが、追加の情報を探すことでした。
今回の問題では補助線という、問題を解きやすくしてくれる線を自分で引いて大きな四角形を作っていくことがポイントでしたね。
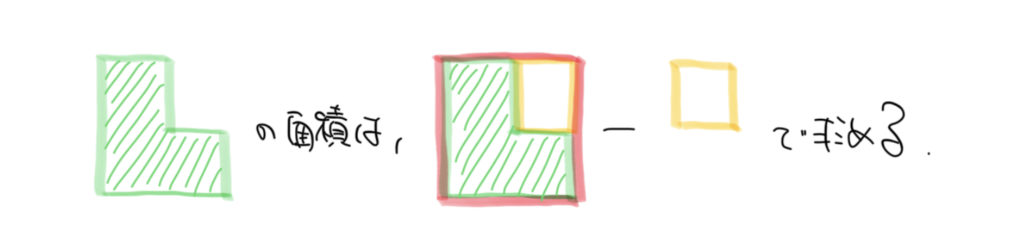

そしてこの足りない面積の考えは例題のつるかめ算などでも使われましたね。

この面積図をきちんと書く練習と補助線を引いて問題を解いていく特訓をしていけば面積図の基礎が身につくと思います。
さて、ここから類題を解いていきましょう!!