【中学受験算数】苦手の生徒の多い「割合と比」を線分図を書いて攻略！兄弟の所持金の変化から２人の持っていた金額を求めよう！

はじめに

みなさんおはようございます！
今日は中学受験算数の「割合と比」から問題を出していきます！

いままで「さんすうがく」で教えてきた比や線分図を使って問題を解いてみましょう！
それではいつも通り、まずはカンタンな問題から線分図を書く練習をしてみましょう。

まずは線分図を書く練習をしてみよう

問題：次の①、②、③の内容を図にしなさい。

①AさんとBさんの所持金しょじきんの比は8:3です。
②そのとき、AさんはBさんに1000円わたしました。
③すると、AさんとBさんの所持金しょじきんの比が7:4になりました。

それでは図を3つ、書いていきましょう！！！

線分図の書き方

①の線分図

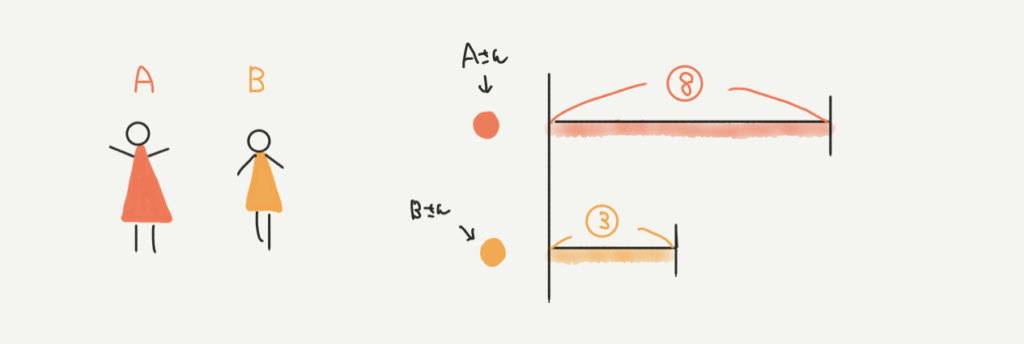
まずは①の線分図を書いてみましょう。
むずかしいことはありません。
まずはイメージするために、AさんとBさんの絵をかいてみてもいいですよ！

AさんとBさんの所持金しょじきんの比が8:3なので、Aさんの金額を⑧、Bさんの金額を③と表すことができます。

②の線分図

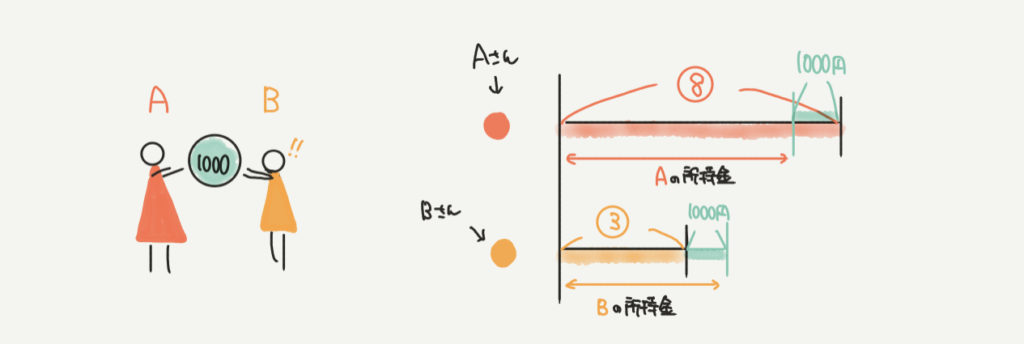
続いて、AさんがBさんへ1000円わたしたときの図を書いてみましょう。
Aさんの⑧から1000円引かれた線分図がかけますね！
そして一方で、Bさんは③に1000円プラスされるので、Bさんの所持金を③＋1000円と考えることができます。

③の線分図

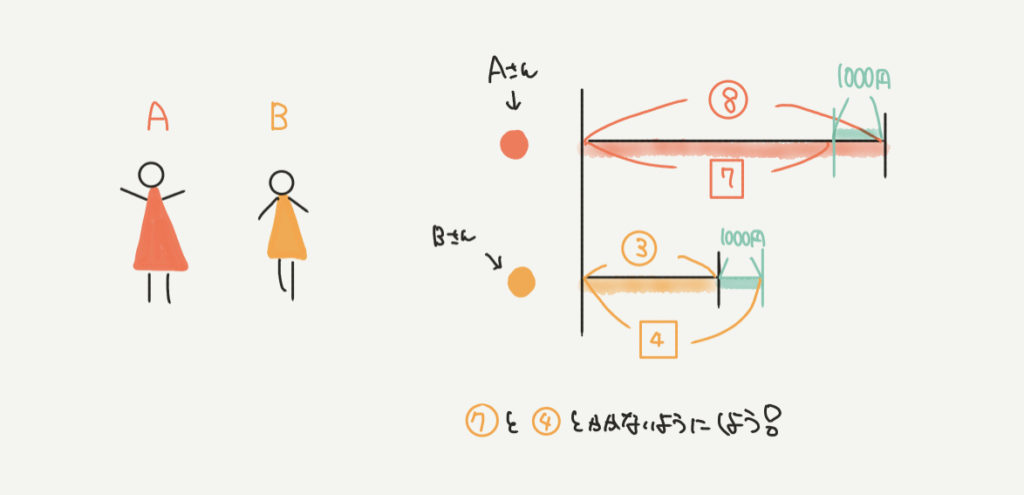
最後だけ少しむずかしいですよ。
この②の線分図の1000円わたした後のAさんとBさんの所持金しょじきんを見ていくと、
7:4と問題文でいわれていますので、□の7と□の4と書くことができました。

ここまでかければ問題なく、今日の問題にチャレンジできると思います！
記号を別で書かないといけない理由がわかっている受験生は下の内容は飛とばして問題を解いていて大丈夫だいじょうぶです！

算数を得意にするコツ、なんで記号を同じにしてはいけないの？

さて、上の線分図で、①でかいた比と③でかいた比を同じにしてしまった受験生はいますか？
これ、記号を同じにしてかいちゃうとまちがった答えを出してしまう場合があります。
どういうことでしょう？

比を同じ記号で書いてはいけない理由

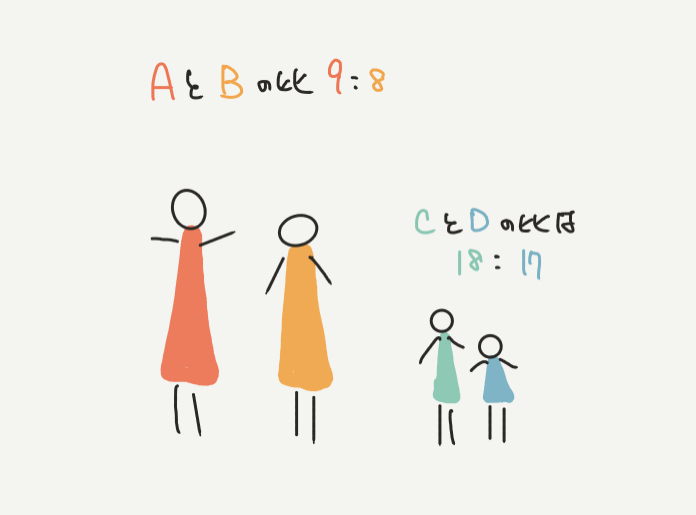
たとえばA、B、C、Dの4人がいたとします。
どう見ても今回はAとBの方がCとDよりも大きいですよね？

それぞれの身長しんちょうの比は、
A:B＝9:8
C:D＝18:17 です。

これを同じ記号（○）で表してしまうと…

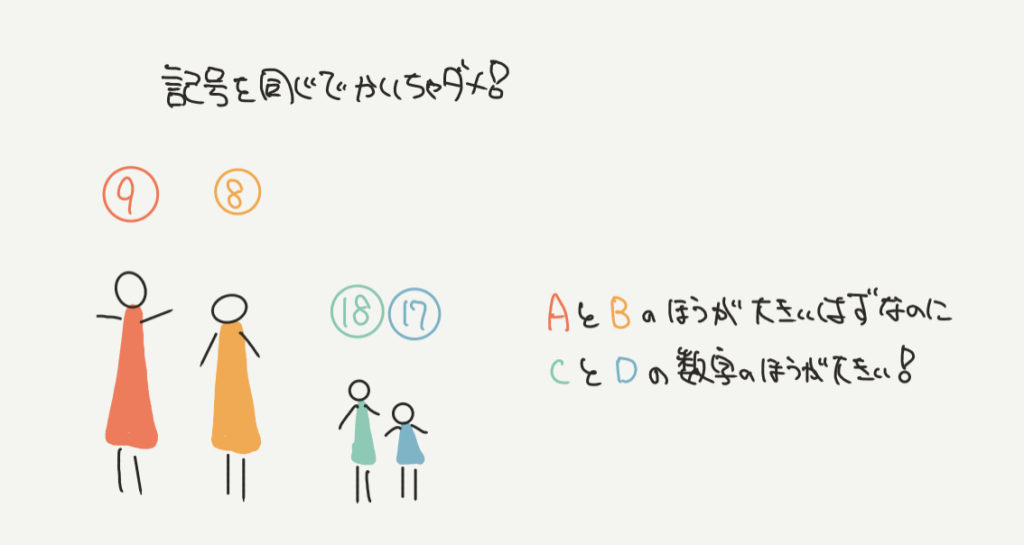
⑨、⑧、⑱、⑰となってしまい、なぜかCとDの身長しんちょうの方が大きくなってしまいます。
なぜこのやり方がいけないかというと、比くらべる基準きじゅんによって記号を変えていないからです。

比は比くらべる基準きじゅんによって記号を変えないといけない！

本当はAとBで身長しんちょうを比くらべているので、Aの身長しんちょうを⑨とすると、
Bの身長しんちょうが⑧になる、というのがA:B＝9:8の意味になります。
一方で、CはDと身長しんちょうを比くらべているので、比くらべる基準きじゅんが違ちがいますよね？

なので、記号を別でかかないと基準きじゅんがバラバラの数字で大きさを比べてしまうのでまちがった答えを出してしまうことになります。
さて、ここまでが例題でした。

ここまで読んでもまだ理解できないという受験生は、とにかく同じ記号で問題を解くのは気をつけよう、ということだけまずは覚えておいてください！

ここからは実践問題じっせんもんだいに挑戦です！

問題に挑戦ちょうせん！

はじめ、兄と妹の所持金の比は5:2でしたが、兄が妹に500円あげたので、2人の所持金の比が4:3になりました。
はじめの兄の所持金はいくらですか。

解答

この記事を書いている人はこんな人

解説を読んで「 割合と比 」を攻略こうりゃくしよう！

STEP1：問題文を線分図にしよう

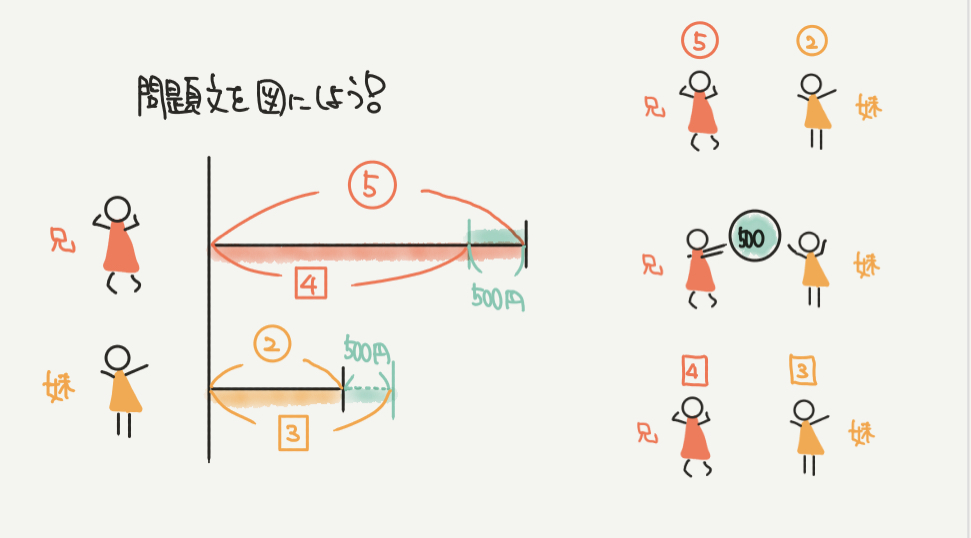
まずは問題文の内容を図にしましょう！
絵にすると、右がわのようになります。

線分図をかくときの注意点は、例題でも説明した通り、記号を同じもので書かないようにすることです。

↑今回は○の数字がもともと持っていた所持金しょじきんが基準きじゅんで、□が500円渡わたした後のお金が基準きじゅんになっています。

STEP1のこの図をきちんとかければ、あとは計算するだけなので、
まずはこの線分図を確実にかけるようにしましょう！！！

STEP2：同じところがない！なら作ろう！！

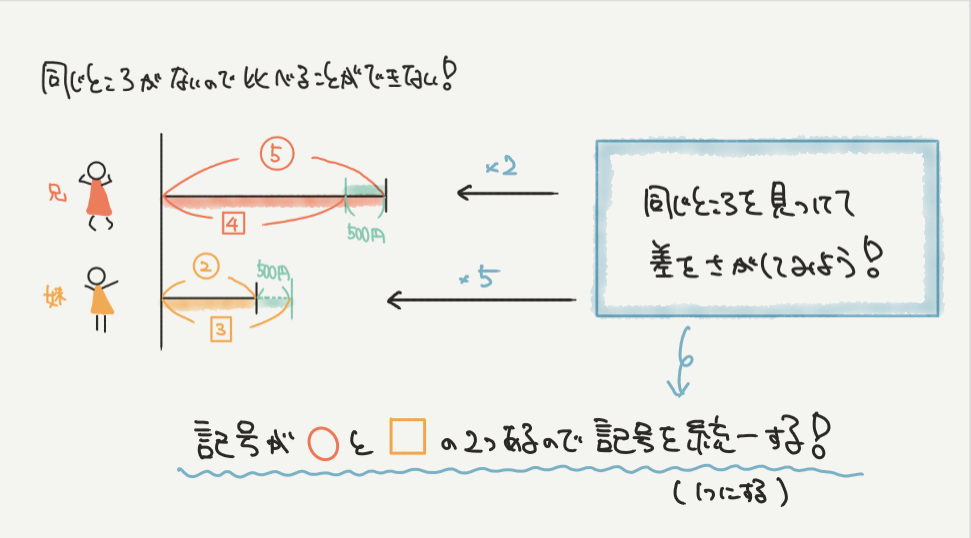
図をかいても先に進めない！！とはじめは思うかもしれません。
でも、心配しないでください。

この図から、同じところがないのなら作ってしまえばいいのです。
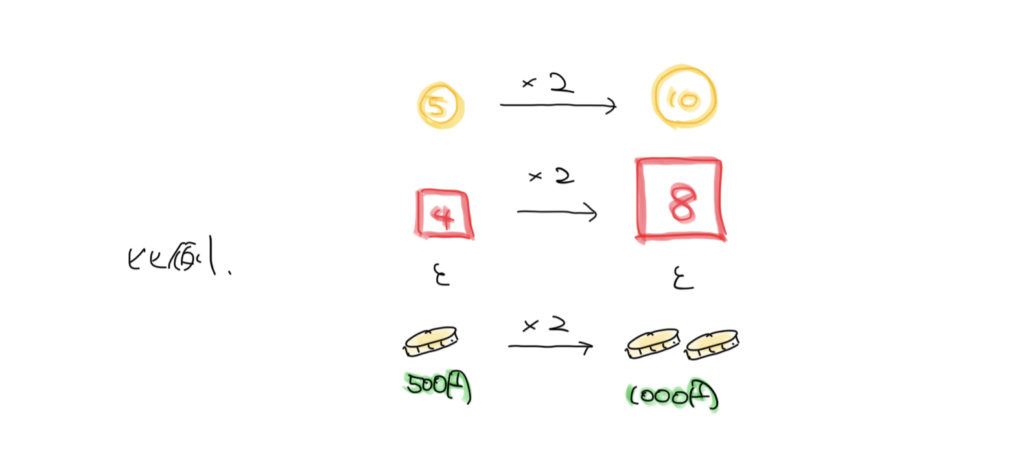
たとえば、今回は⑤と②を⑩で同じにしたいので、兄の図を2倍、妹の図を5倍にして見ましょう。

すると兄の⑤が2倍されて⑩になり、
同じく妹も②が5倍されて⑩になりますね！

どういうことかわからない受験生は、STEP3を見てみてください！

↑これが「同じところを見つける、作る」という算数の大事な考え方になります。

算数の大事な考え方

STEP3：同じところを作る

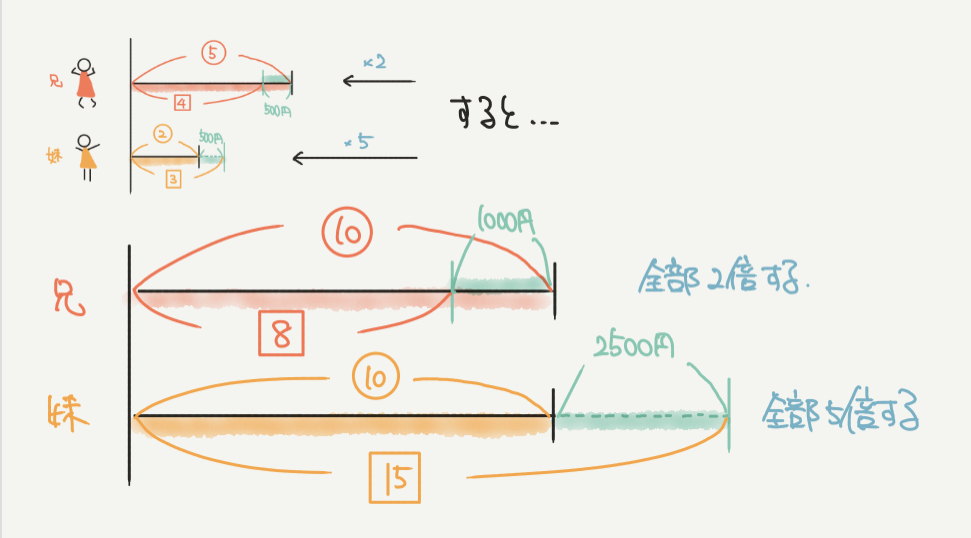
同じところを作ると上の図のようになります。
今回は兄の所持金⑤と妹の所持金②を⑩にそろえて同じものを作りました。

兄の所持金しょじきん（⑤）を2倍するということは、□の4と500円も2倍することになります。これは比例の復習ですね。
同じようにに、妹の所持金しょじきんを5倍したので、□の3と500円も5倍しないといけなくなります。

STEP4：同じところから差を見つけて解いていきましょう

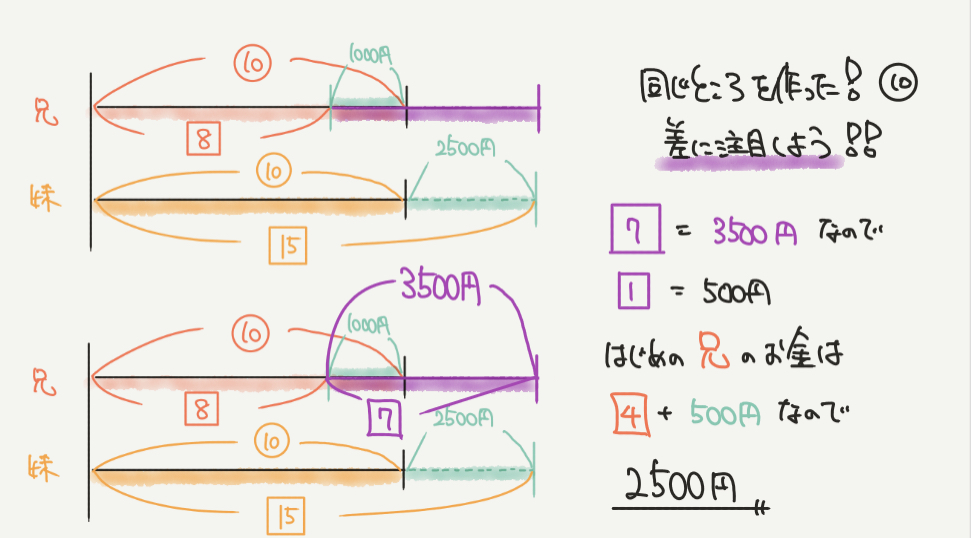
ここで兄と妹の線分図の部分を⑩とそろえたことで、
□の15と□の8の差（□の7）が3500円であることがわかります。

よって、
□の7＝3500円なので
□の1＝500円になります。

答えはもともとの兄の所持金しょじきんなので、もともとの線分図から答えを求めます。
2倍した線分図の答えを答えてはいけませんので、注意してくださいね！！

兄のもとの所持金しょじきんは、□の4＋500円なので、
500円×4+500円＝2500円となります！

兄弟の所持金の変化から２人の持っていた金額を求める問題のまとめ

今回の問題で大事なポイント

比の考え方（はじめに）
・比は何を基準きじゅんにするかで考えよう！
線分図の書き方（STEP1）
「同じところを見つける、作る」考え方（STEP2）

以上が本日の問題でした。おつかれさまでした！！
少しむずかしい問題でしたが、きちんと解けましたか？

むずかしい分、例題や説明をいつもより多く、わかりやすくしてみたのでぜひ読み返して復習してみてください。
大事なのは、読んで終わりにするのではなく、解説を自分でかけるようにすることです！

書いてあることを理解するのと、かいてあることを自分でやれることは全く違います！！
必ず自分でも解けるように、解説の図をノートに書くようにしましょう！

その他の単元の問題の復習はこちらから！