目次
はじめに
みなさんこんばんは!「さんすうがく」の赤い小人です。2022年もがんばっていきましょう!
「 数の性質 」の問題、今回は最小公倍数と最大公約数について勉強していきましょう!!
「 数と性質 」の復習はこちらから!
最小公倍数と最大公約数に関する復習を下の問題にのせています!
まだ最小公倍数と最大公約数の解き方が不安だという受験生はこちらから復習しておきましょう。
ここまでは大丈夫だぜ!という受験生は飛ばしちゃってOKです。
最小公倍数と最大公約数の求め方

まずは最小公倍数と最大公約数について求め方の復習をしておきましょう。
最小公倍数・・・ある2つ以上の整数に共通する最も小さい公倍数
最大公約数・・・ある2つ以上の整数に共通する最も大きい約数
たとえばこの図では、36と48の最小公倍数と最大公約数について計算しています。
まずは2つの数に共通する約数で割り算をしていきましょう。
約数は2、3、5となるべく小さい数から割っていくと解きやすいですよ!
すると、2、2、3で割り算することができました。
ここから最小公倍数と最大公約数を求めていきます。
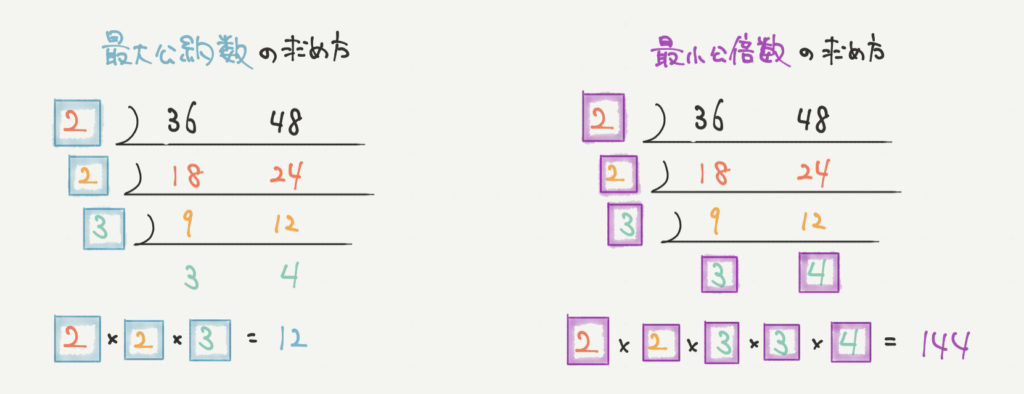
最大公約数は割った約数を全てかけ算した値になります。
たとえばこの場合だと、2×2×3=12が最大公約数です。
最小公倍数は割った約数とその商をかけ算した値になります。
たとえばこの場合だと、2×2×3×3×4=144が最小公倍数です。
今日解く問題では、この2つの求め方を使って計算する必要があります。
がんばって解いて行きましょう〜!
「 数の性質 」の問題に挑戦!
ある整数xと84の最大公約数は21で、最小公倍数は252です。整数xを求めなさい。
解答は次のページから!
塾ナビ 口コミランキング1位 AIを使ったの最新の学習システム!
信頼できるオンライン学習塾をお探しの保護者様へ。松陰塾のオンライン学習「松陰スタディ」では、43年以上の実績を持つ個別指導法で、小・中学生の5教科をサポートします。AI技術を駆使した12万問題の学習システムで、お子様一人ひとりに合わせた最適な学習プランを実現、自立学習の習慣を身につけさせます。無料相談、資料請求も実施中です!