目次
はじめに
みなさんこんにちは!!「
さんすうがく」の赤い小人です。
本日も「 数の性質 」の問題にチャレンジして行きましょう〜〜!
「 数と性質 」の復習はこちらから!
今回の問題では、素数という言葉が出てきます。
素数というのは2や3のように、1とその数でしか割れないような数のことでしたね!
素数に関する勉強は下の問題からもできますので、時間のある受験生はまずこちらの問題から解いておくと理解しやすくなると思います。
ここまでは大丈夫だぜ!という受験生は飛ばしちゃってOKです。
素因数分解ってなに?

まずはこの問題で出てくる素因数分解という言葉について理解しておきましょう。
素因数分解とは、ある整数をかけ算の形で表したものです。
たとえば、6という数字は2×3=6と、2つの素数のかけ算で表すことができます。
また8という数字も、2×2×2=8と素数のかけ算で表すことができます。
このように整数を素数のかけ算で表す練習をしてみましょう。
ちなみに2×4=8と表すことができますが、4は素数ではないのでまちがいです。

このようなまちがいをしないために、素因数分解するときのやり方を2つにまとめています。
①まず初めに小さな素数から順番に割り算できないか調べること
②割った数をかけ算の形にすること
この2つのルールを守るように計算してみて下さい。
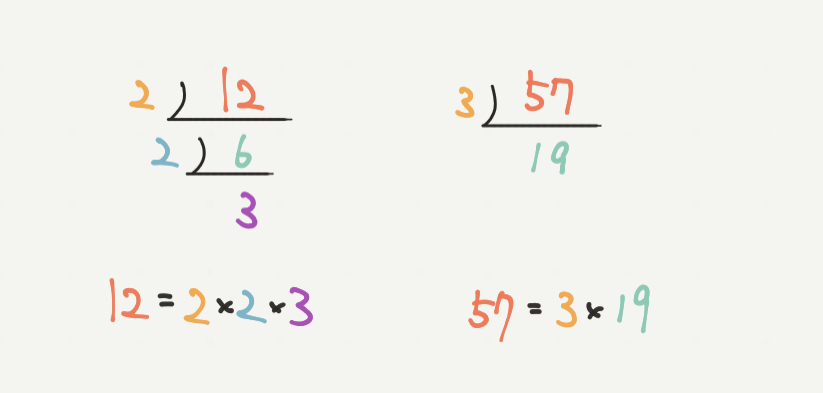
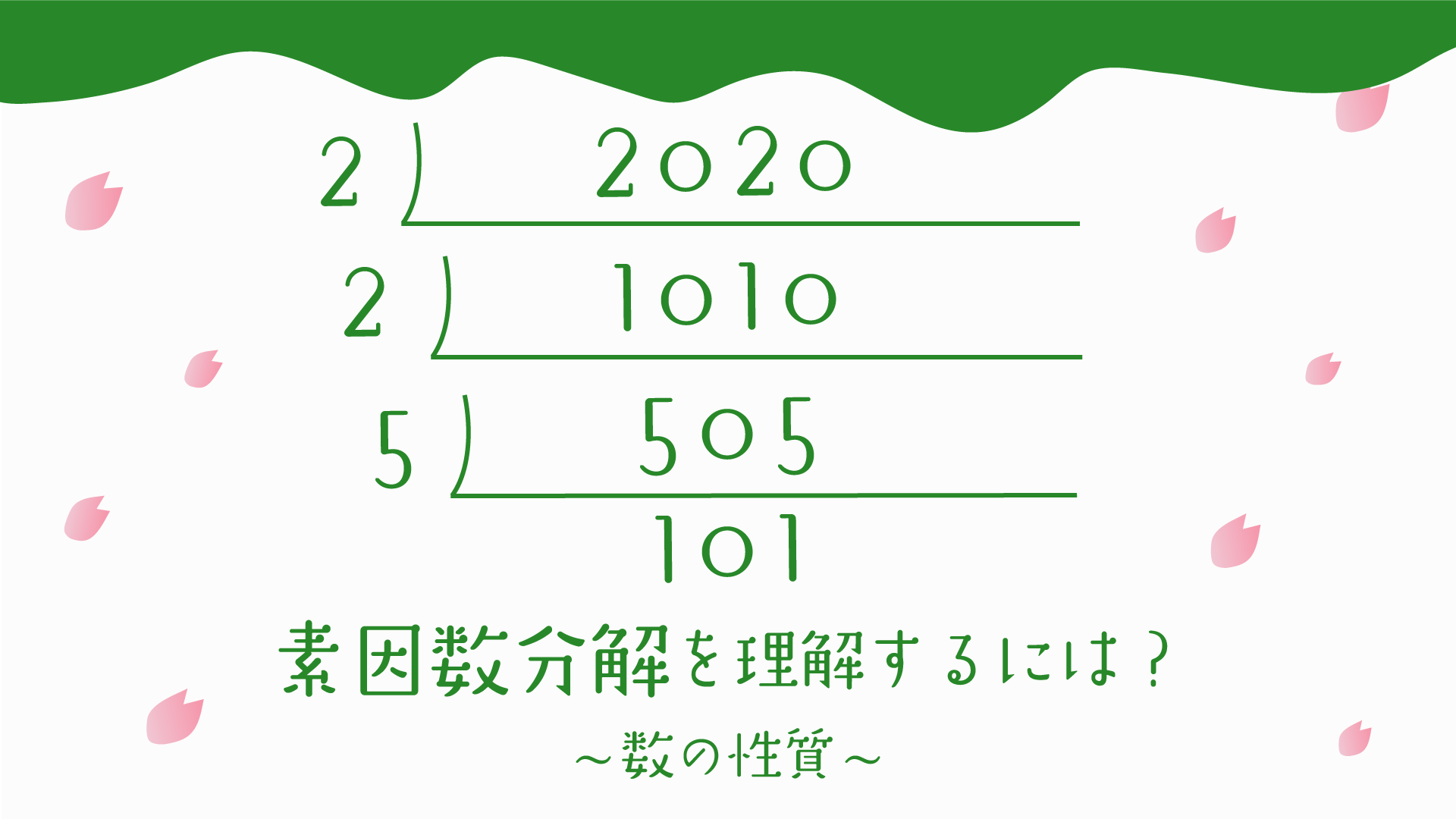
たとえば、12という数字を小さな素数2から順番に割っていくと、
12=2×2×3と表すことができます。
また、57という数字は2では割れないので、次に小さい素数3で割ると、
57=3×19と表すことができました!
さて!それでは問題に挑戦してみましょう〜!!
「 数の性質 」の問題に挑戦!
2020を素因数分解しなさい。
解答は次のページから!