目次
解答
2020＝2×2×5×101
解説を読んで「 数の性質 」を攻略しよう！
STEP1：素数で割るときは倍数の性質を覚えておくと楽！
素因数分解は素数で割れるかどうかを確かめる必要があります。
なので、2の倍数や3の倍数、5の倍数の性質を覚えておくと、かんたんにその数が割れるかどうかを判別できます。
2020は偶数なので2の倍数ということがわかりますし、下1ケタが0なので5の倍数でもあることがわかります。
こんな形で頭でイメージしながら割り算してみましょう。
倍数の性質の問題はこちらから復習できます！！
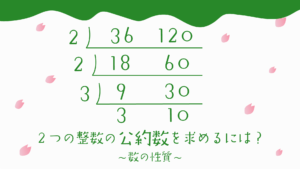
STEP2：2020を小さい素数で割っていこう
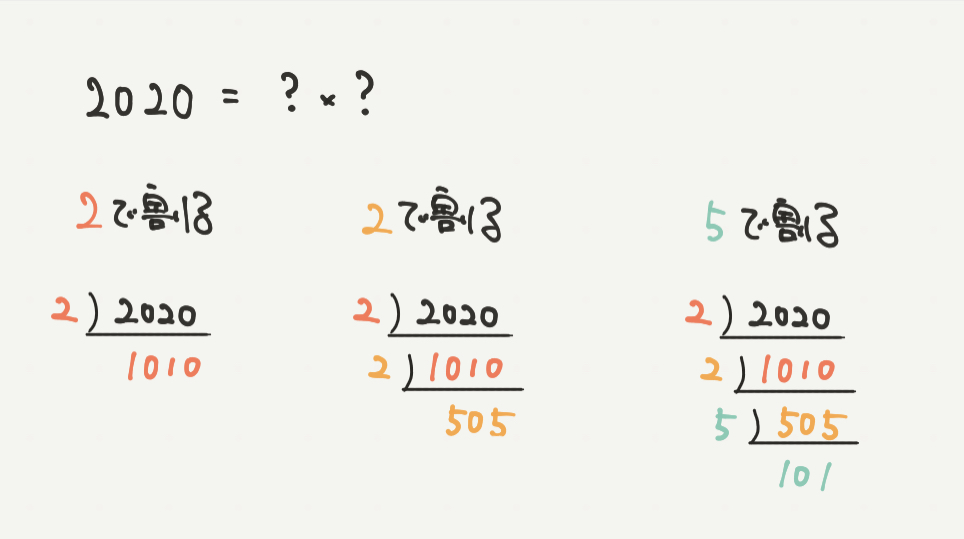
2020を2で割っていくと、
2020÷2＝1010となります。
1010も2で割れるので、
1010÷2＝505
505は2でも3でも割れないので次に小さい素数5で割ると、
505÷5＝101となりました。
101が素数かどうかはわかりませんが、÷19や÷23くらいまで計算してできなさそうなら素数ということにしていました。
STEP3：割った数を計算式に入れて答えを出そう
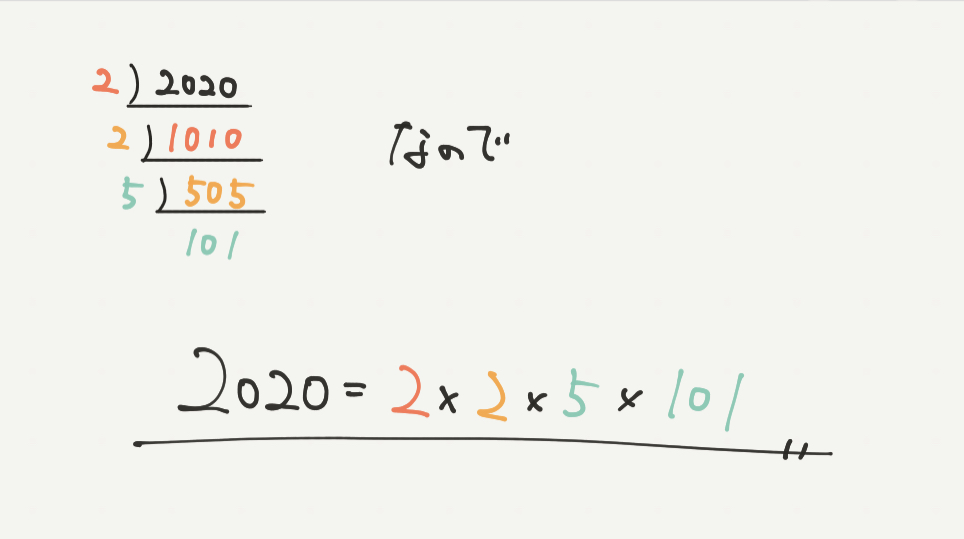
割った数とその商をかけ算すると、
2020＝2×2×5×101
と素数のかけ算で表すことができました。
STEP4：2021よりも大きい数字の因数分解も覚えておこう
ちなみに受験ではよくその年の数字が使われます。
今回の問題のように2020を素因数分解させたり、計算問題に2020を出したりと出題のされ方は様々です。
この問題を作ったのが2020年だったので、2020という数字を使いました。2021年や2022年の素因数分解も覚えておくと楽かもしれませんね！
2021＝43×47
2022＝2×3×337
2023＝7×17×17
2024＝2×2×2×11×23
素因数分解を理解するときのまとめ
「 数の性質 」の問題で大事なポイント
- 素数に関する考え方
- 素数は1とその数でしか割ることのできない数
- 例）2、3、5、7、11、13、17、19・・・
- 素因数分解の考え方
- ある整数を素数のかけ算で表す考え方のこと
- 例）12＝2×2×3、400＝2×2×2×2×5×5
以上で今日の問題は終わりです！
最後まで読んでくれてありがとうございました！！
次の問題で会いましょう！！！
