目次
はじめに
みなさんこんばんは!!
「さんすうがく」の赤い小人です。
今日も「 数の性質 」の問題ですね!よろしくお願いします。
今日の問題は少しむずかしいのでいつもよりていねいに解説しますね!
「 数と性質 」の復習はこちらから!
もうここは大丈夫だぜ!という人はここの部分は飛ばしてしまってOKです!
今回の問題では約数を求める方法と、割り算の仕組みについて理解しておく必要があります。
なのでこの2つの問題は絶対にできるようにしておいて下さい!!
公約数に関するていねい解説
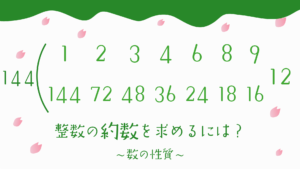
この記事では3つの数の公約数を求める問題が出てきます。
1つ1つの整数の約数を数え上げて、同じ数を調べるやり方でも公約数を求めることができますが、効率が悪いです。
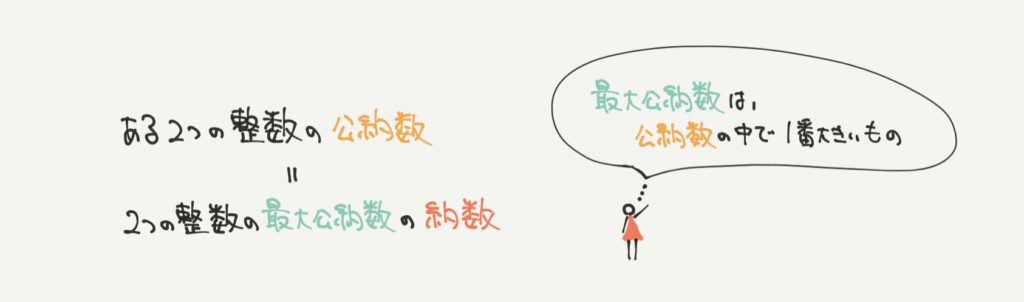
公約数は最大公約数の約数ですので、
ここでは、最大公約数の約数を求める方法で公約数を調べ上げていきます。
ちなみに最大公約数とは公約数の中で最も大きな数のことです。

最大公約数の求め方は上の図を参考にしてみて下さい。
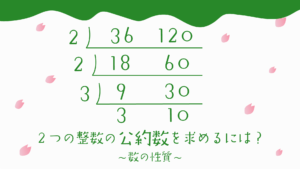
たとえば36と120という数の公約数を求めたいとき、
共通する約数で割算していきます。
はじめは2で割っていき、さらに2で割り、最後に3で割るとこれ以上共通する約数がなくなります。

ここまで書ければ36と120の最大公約数を求められます。
割った約数をかけ算していくと、2×2×3=12となり、
12が最大公約数と計算することができました。
公約数は最大公約数の約数でしたので、
36と120の公約数は最大公約数(12)の約数である、1,2,3,4,6,12となりました。
少しむずかしいと思いますが、この部分がとても大事なのでしっかり理解するようにしましょう。
「 数の性質 」の問題に挑戦!
98を割ると2あまり、125を割ると5あまり、163を割ると3あまる整数を全て求めなさい。
解答は次のページから!