目次
はじめに
みなさんこんばんは!!
「さんすうがく」の赤い小人です。
今日も「 数の性質 」の問題にチャレンジしましょう。
「 数と性質 」の復習はこちらから!
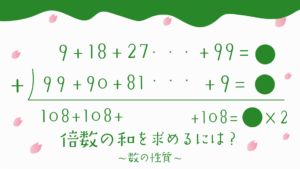
「 数の性質 」の問題ももう半分が終わりました。
これまでの問題をいくつか書きましたので、復習がまだできていない受験生はこちらから解くようにしましょう。
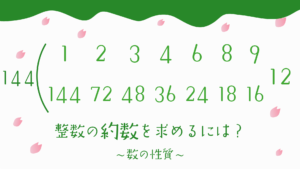
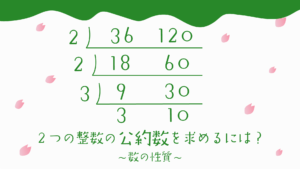
2つの整数の公約数を求める問題はこちら!

割る数と余った数から当てはまる整数を求める問題はこちらから!

約数が2個しかない整数を求める問題はこちらから!

図形を使って正方形を作るには?
今回の問題では最小公倍数という言葉が出てきます。
最小公倍数とは、ある2つ以上の整数に共通する倍数の数のことです。
まずは下の絵を見てみましょう。
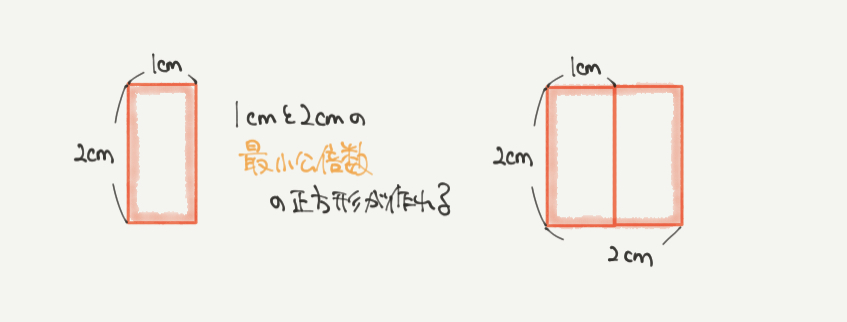
長方形は一辺が1cmと2cmの図形です。
この図形を組み合わせて正方形を作るとき、作ることのできる最もかんたんな図形が一辺2cmの正方形です。
このとき、正方形の一辺の長さは1cmと2cmの最小公倍数の数になります。
正方形を作るには、図形の長さの最小公倍数を考えればいいんですね。
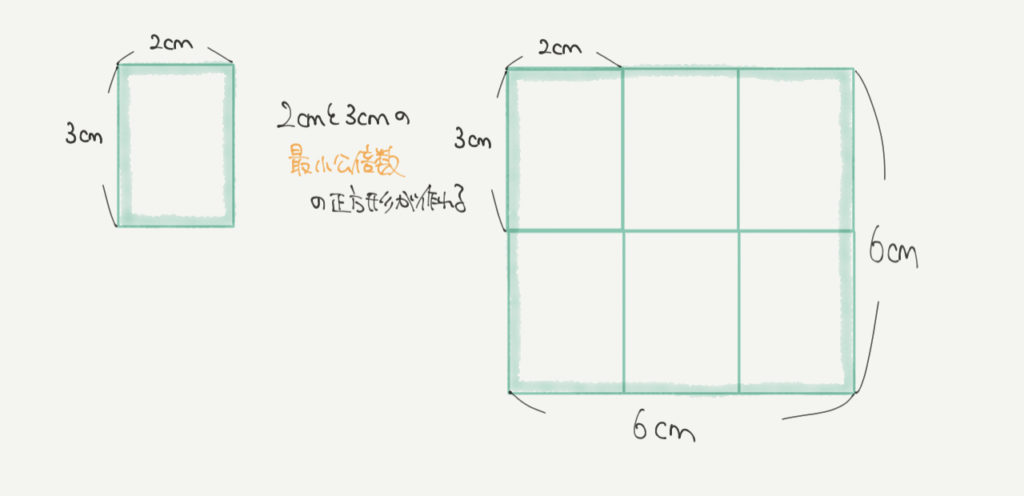
同じように、こちらの長方形は一辺が2cmと3cmになっています。
2cmと3cmの最小公倍数は6cmなので、今回は一辺6cmの正方形を作ることができます。
図形の数が一番小さくなるように正方形を作るとき、その正方形の長さは図形の最小公倍数の長さとなります!
(今回は2cmと3cmの図形を使って6cmの正方形を作りました。)
今日の問題のポイントを勉強したところで、さっそく問題を解いていきましょう。
「 数の性質 」の問題に挑戦!
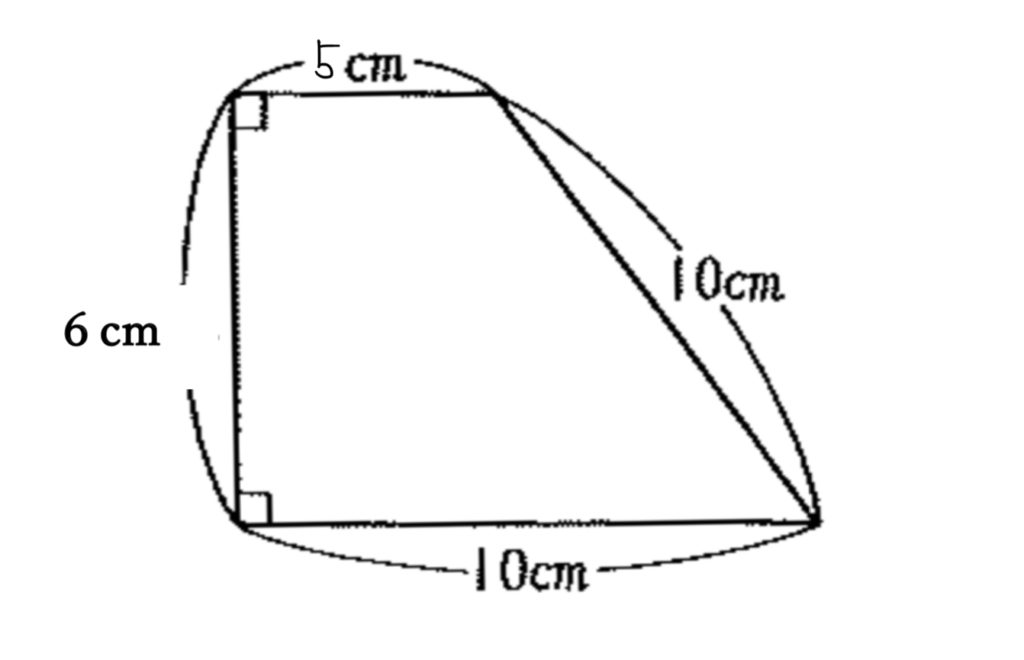
下の図のような台形の紙がたくさんあります。この紙をすき間なく並べて、出来るだけ小さな正方形を作ろうと思います。台形の紙は全部で何枚必要ですか。
解答は次のページから!