はじめに
みなさん新年あけましておめでとうございます!!
家でまったりしている「さんすうがく」の赤い小人です。
「 数の性質 」の問題、今回は倍数の性質について勉強していきましょう!!
倍数の性質ってどういうものなんですか?
倍数の性質は、その倍数に見られる特徴のことです。
実際にヒントで解説していますので、よく読んでみましょう。
「 数と性質 」の復習はこちらから!
ここまでは大丈夫だぜ!という受験生は飛ばしちゃってOKです。
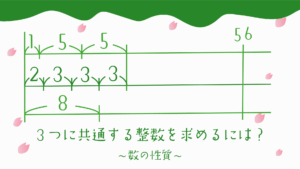
割る数と余った数から当てはまる整数を求める問題はこちら!

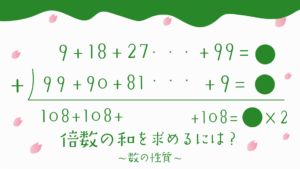
○を割ると□あまる整数を求める問題はこちらから!

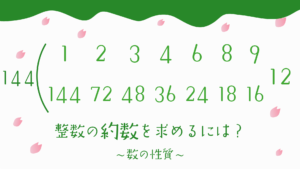
約数が2個しかない整数を求める問題はこちら!

倍数の性質を勉強しよう!
まずは倍数の性質について勉強していきましょう。

2の倍数の性質
2の倍数の性質は偶数であることです。
偶数は下1ケタが0,2,4,6,8のことです。
たとえば、230,14,9092などの数は2の倍数です。
3の倍数の性質
3の倍数は各位の数の和が3の倍数であることです。
たとえば、
333は3+3+3=9(3の倍数)なので、
333は3の倍数となります。
4の倍数の性質
4の倍数の性質は下2ケタが4の倍数になることです。
たとえば、
5020は下2ケタが20で4の倍数なので、5020は4の倍数となります。
5の倍数の性質
5の倍数の性質は下1ケタが0か5になることです。
たとえば、345は下1ケタが5なので345は5の倍数です。
同じように2980も下1ケタが0なので、2980も5の倍数です。
6の倍数の性質
6の倍数は2の倍数でもあり、3の倍数でもあるのでそれぞれの倍数の性質を合わせて持っています。
なので、6の倍数の性質は偶数であり各位の数の和が3の倍数であることです。
たとえば、
156は偶数で各位の数の和が1+5+6=12(3の倍数)なので6の倍数となります。
8の倍数の性質
8の倍数の性質は下3ケタが8の倍数であることです。
たとえば、10808は下3ケタの808が8の倍数なので、10808は8の倍数です。
9の倍数の性質
最後に9の倍数の性質です。
9の倍数の性質は各位の数の和が9の倍数であることです。
たとえば、
693という数は各位の数の和が6+9+3=18(9の倍数)なので、693は9の倍数となります。
7の倍数の性質もありますが、むずかしいので普通に7で割り算した方が早いです!!
さあやってみましょう!!
「 数の性質 」の問題に挑戦!
次の問いに答えなさい。
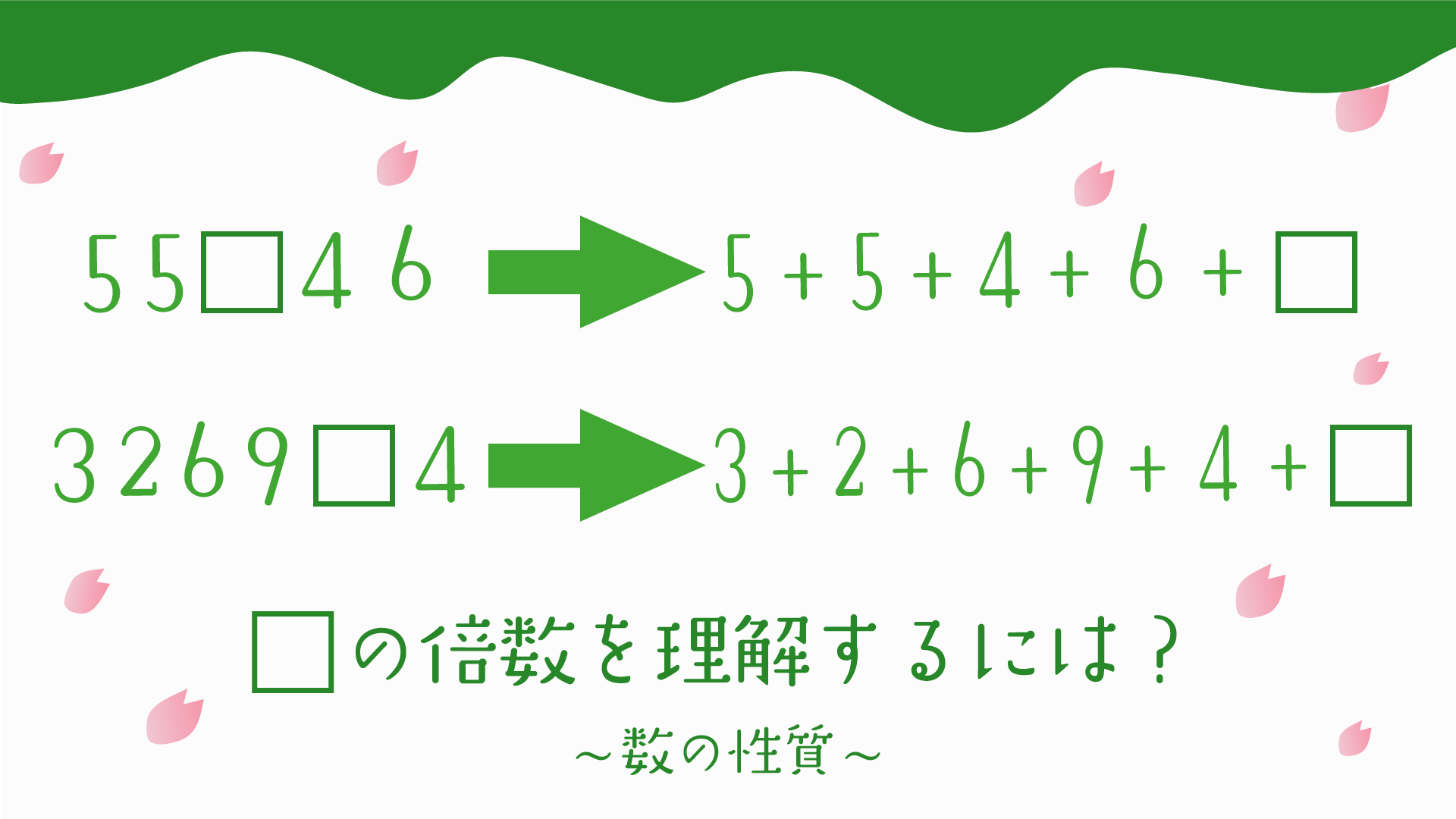
① 百の位がわからない5けたの9の倍数55□46があります。□に当てはまる数字を全て求めなさい。
② 十の位がわからない6けたの4の倍数3269□4があります。□に当てはまる数字を全て求めなさい。
解答は次のページから!