【中学受験攻略】平面図形の基本「相似」を利用して木の高さを計算しよう！

2024年3月3日

はじめに

みなさんこんにちは！
「平面図形」の問題もあとわずかです。残り数問がんばっていきましょう！

今日は「相似そうじ」がテーマになっています。
さっそくヒントから「相似そうじ」について説明していきますので、ついてきてくださいね！

「相似そうじ」は平面図形の問題を解く上で超大切な考え方なので今日でマスターしちゃいましょう。

相似ってなに？

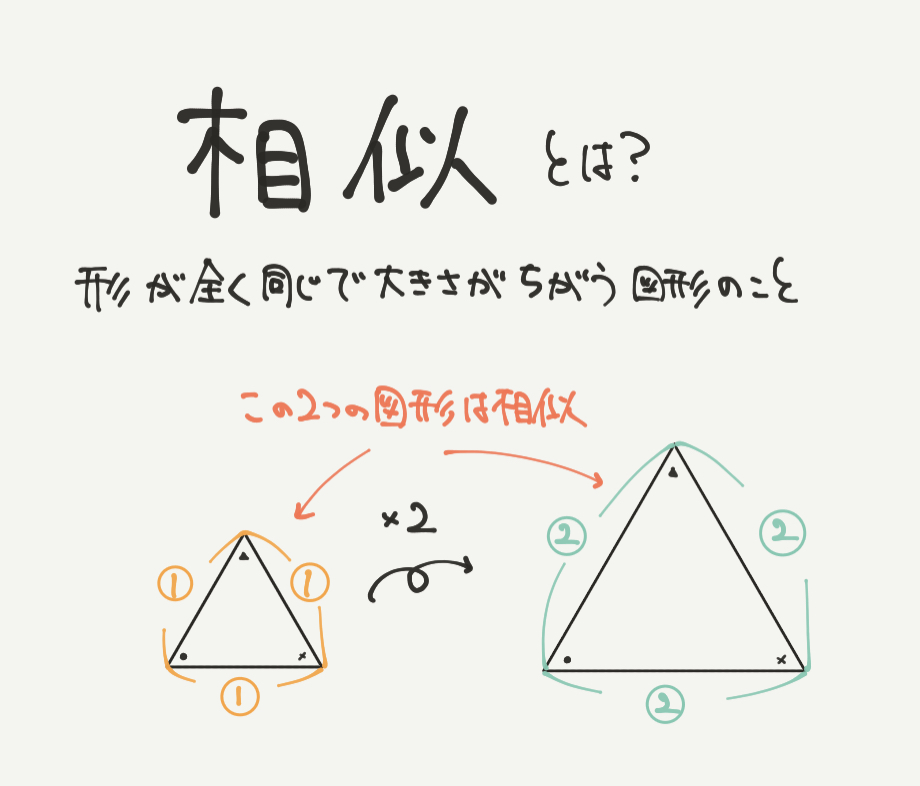
相似そうじとは、形が全く同じで大きさがちがう図形のことです。
たとえば、上の三角形をみてみると角度がどちらも同じなので、
形が全く同じな三角形であることがわかります。

そして大きさをみてみると、辺の長さが2倍になっているので2つの三角形の相似そうじ比は1:2となりました。

このように、大きさだけがちがう図形のことを「相似そうじ」と言い、
平面図形の問題ではこの考え方を使って問題を解いていきます。

ちなみに大きさも形も全く同じ図形を「合同ごうどう」な図形と言います。

相似な図形と対応する辺の長さ

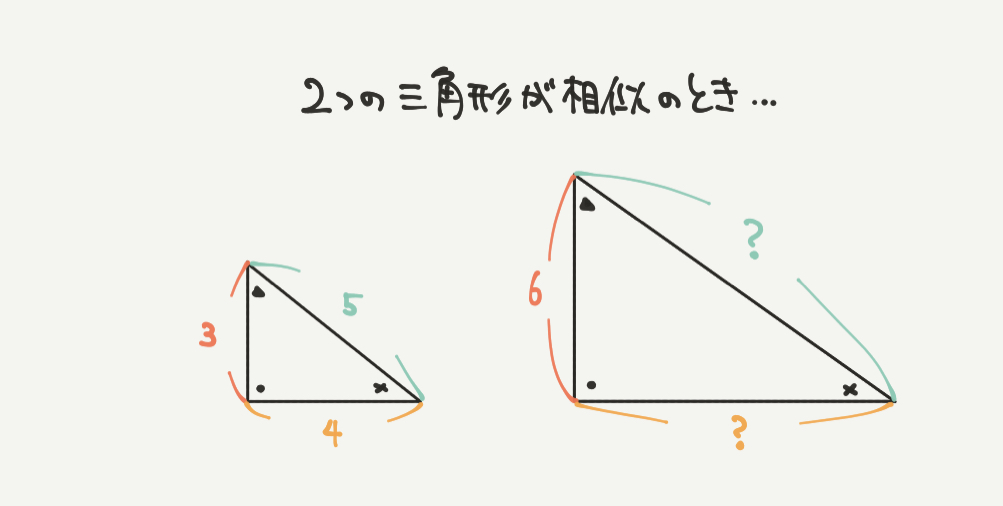
では、相似そうじな図形だとどのように辺の長さを求めることができるのでしょうか？

上の三角形は角度が全部同じなので、相似そうじな三角形であることがわかります。

小さい三角形の辺の長さは3、4、5で大きな三角形の辺の長さは1つしか分かっていません。

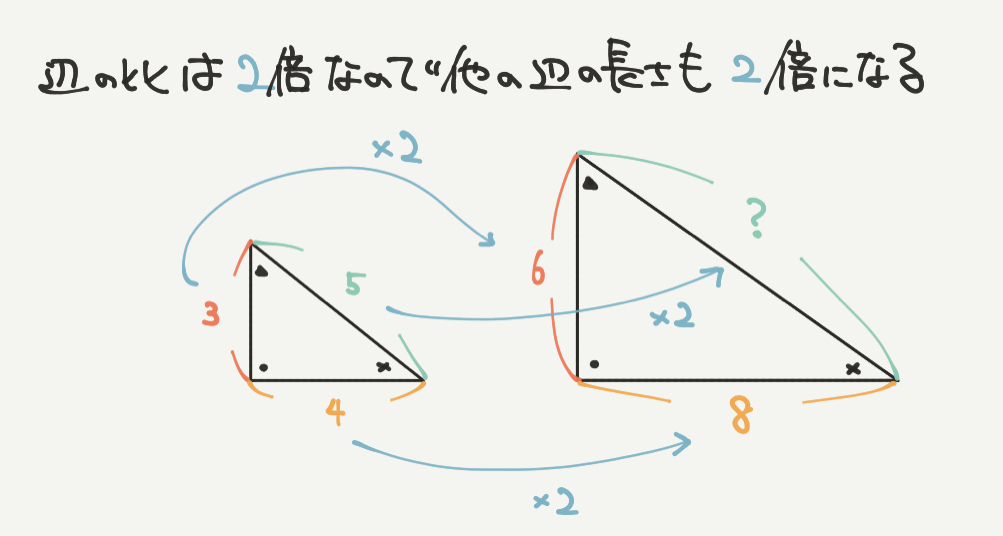
このとき、大きな三角形の6に注目してください。

2つの相似そうじな三角形で辺の長さが3から6へ×2されているのがわかります。

相似そうじな図形は対応する辺の長さが全部同じだけ大きくなるので、赤の辺の長さが×2されれば、

他の黄色の辺の長さと緑の辺の長さも×2されます。

よって
?=10
?=8

というのが求められます。
ここまでが相似そうじの基本です。

今日の問題ではこの考え方を使いながら問題を解いていきましょう。

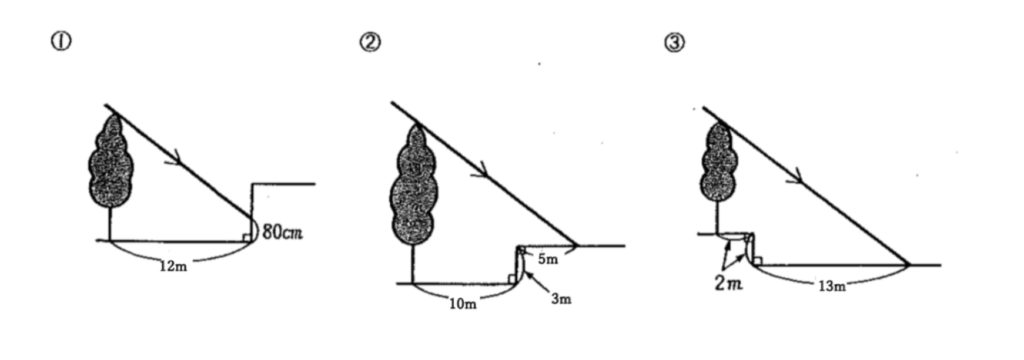
問題に挑戦ちょうせん！

地面に垂直に立てた長さ2mの棒ぼうの影かげの長さが3mのとき、
次の①〜③の図のそれぞれの木の高さを求めなさい。

解答

答えを見るにはここをクリック！

①8m80cm
②13m
③8m

この記事を書いている人はこんな人

解説を見てみよう！

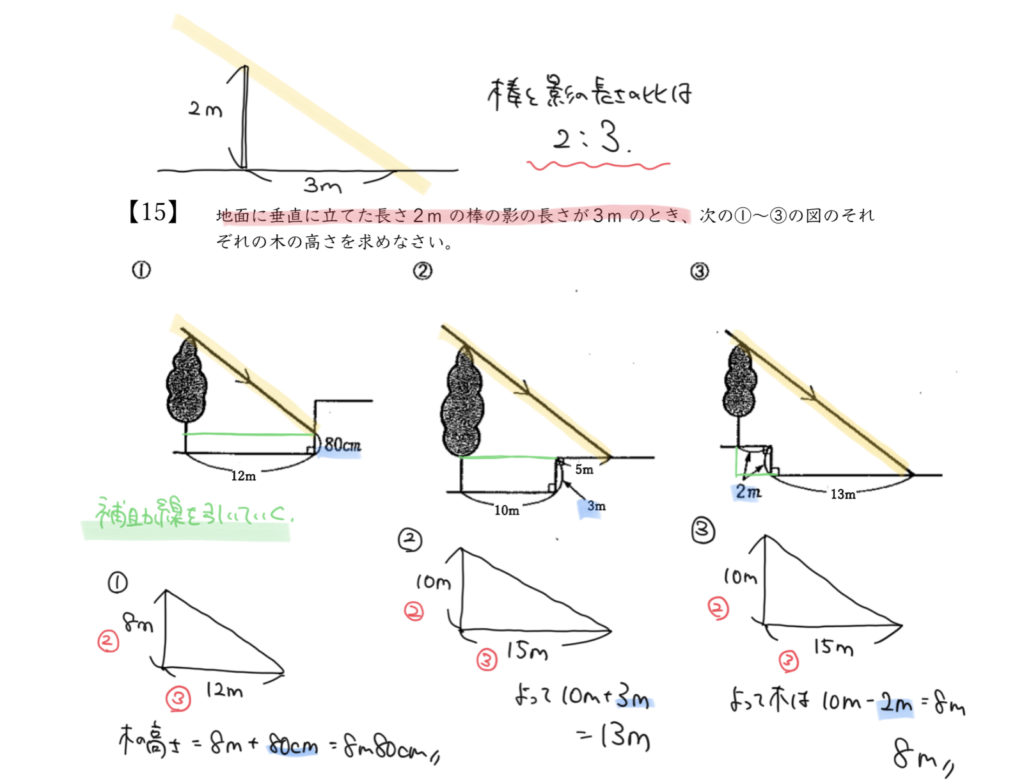
STEP1：問題文から相似比が2:3とわかる

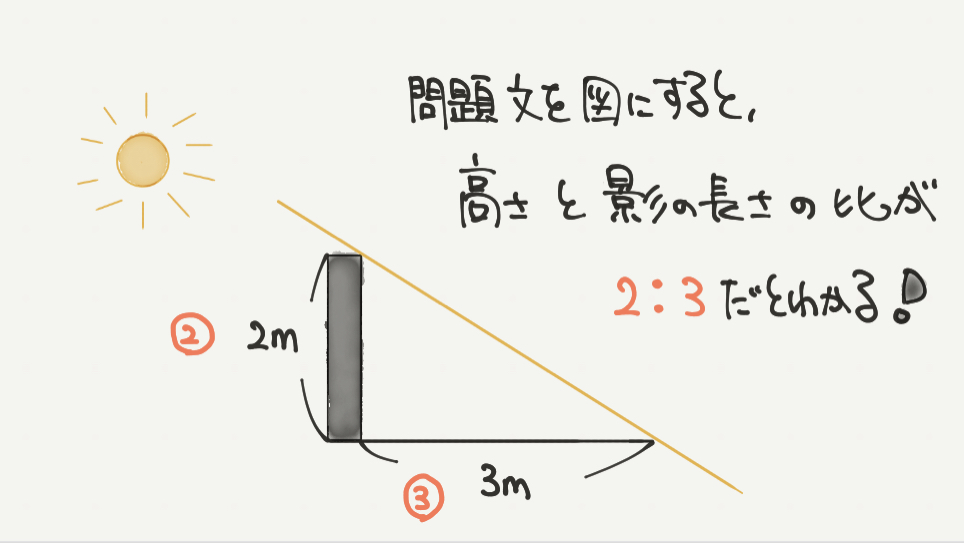
まずは問題文を図にしてみましょう。
高さが2mの棒ぼうを立てると影かげが3mになるので、
たての長さを横の長さの比が2:3となるのがわかります。

太陽が差し込む角度は同じなので、たての長さを影かげの長さの比は必ず2:3になり、
相似そうじな図形であるといえます。
この2:3の情報を使いながら問題を解いていきます。

STEP2：①補助線を引いて木の高さを求めよう

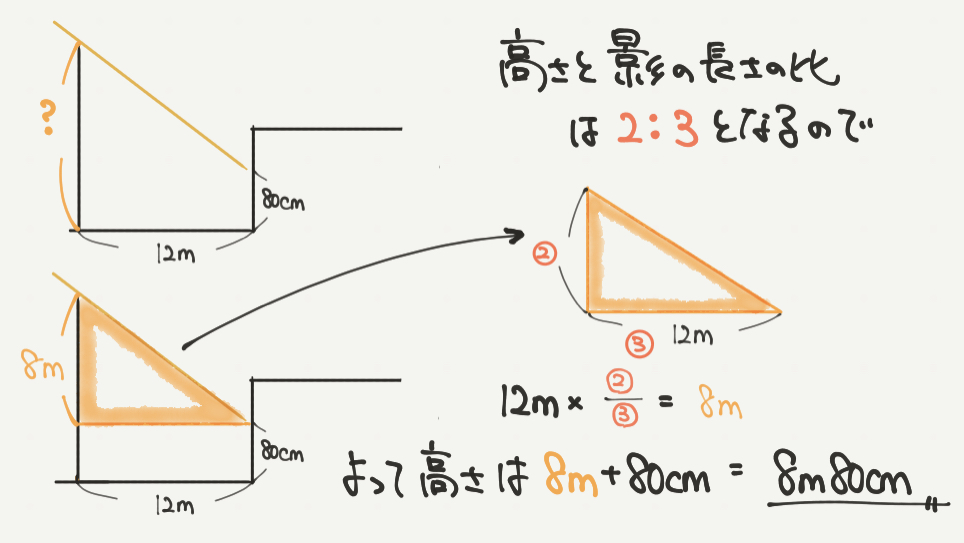
①の問題では補助線を引いて問題を解いていきます。
↑補助線とは？問題を解きやすくするために自分で引く線のことでしたね！

上の図のように横に一本線を引いてみると黄色の三角形ができるのがわかると思います。
この三角形を取り出して、たての長さを求めていきます。

ここで思い出してほしいのがSTEP1で求めた図形のたての長さと横の長さの比です。
たて:横=2:3でしたね！

黄色の三角形の横の長さ（図の③の部分）が12mなので、
②のたての長さは8mと計算できます。

よって求めたい木の高さは8mに80cmをたして、8m80cmとなりました。

STEP3：②補助線を引いて木の高さを求めよう

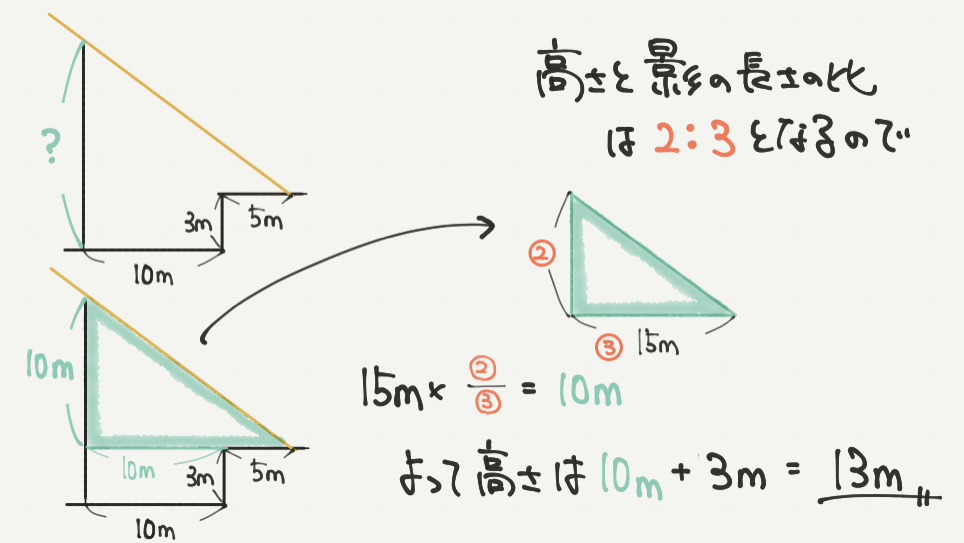
②の問題でも考え方は同じです。これも補助線を引いて解いていきます。
今回は上の図のように横に一本線を引いてみると緑の三角形ができるのがわかると思います。

この三角形を取り出して、STEP2と同じくたての長さを求めていきます。

緑の三角形の横の長さ（図の③の部分）が15mなので、
②のたての長さは10mと計算できます。

よって求めたい木の高さは10mに3mをたして、13mとなりました。

STEP4：③補助線を引いて木の高さを求めよう

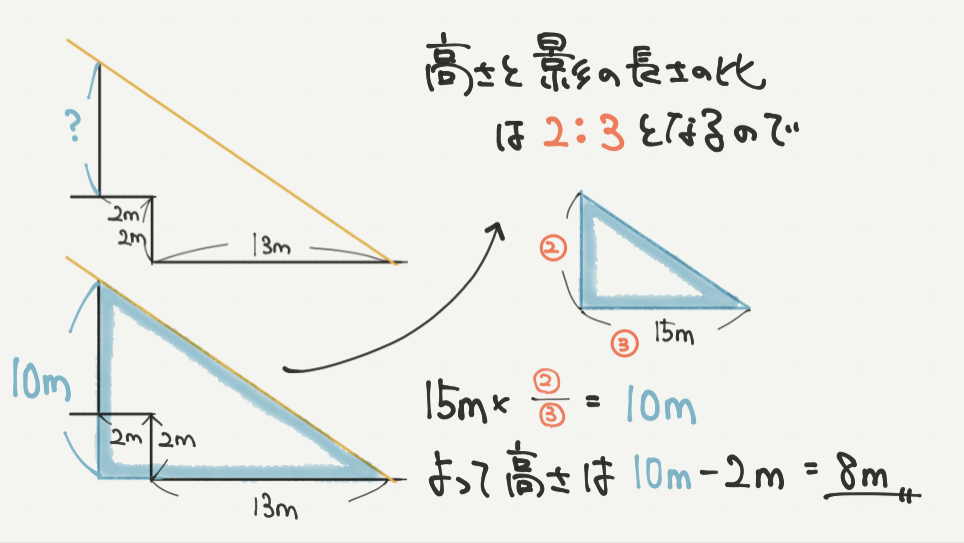
②の問題でも考え方は同じです。実は今回全部の問題で補助線を引いています！

補助線はとても便利ですが、気をつけてほしいのは適当てきとうに補助線を引いてはいけないことです。

問題をたくさん解いて、どこに線を引けば解けそうなのか？をつねに意識しながら
問題を解くようにしてみてください。

この問題では上の図のようにたてと横に一本ずつ線を引いてみると、
青の三角形ができるのがわかると思います。
この三角形を取り出して、STEP2、3と同じくたての長さを求めていきます。

青の三角形の横の長さ（図の③の部分）が15m（13m+2m）なので、
②のたての長さは10mと計算できます。
よって求めたい木の高さは10mから2mを引いて、8mとなります！

影の長さから木の高さを求める問題の解説

今回の問題で大事なポイント

相似そうじの考え方（はじめに、STEP1、2、3、4）
　・相似は形が同じで大きさがちがう図形のことでしたね！
補助線の考え方（STEP2、3、4）
　・どのように線を引くのがいいのか、問題をたくさん解いて感覚をつかんでおこう！

今回は相似そうじに関する大切な問題でした。これが相似そうじの問題の基本です。

この問題では相似そうじの知識のほかに、補助線を引くことも大切でした。
上でまとめた2つのポイントを理解しないと正解できなかったと思います。

補助線の引き方は前の記事でも少し書きましたが、
知らない形から知っている形に変形することが重要でしたね。
↑今回はでこぼこの形から三角形を作るように線を引いてみました。