はじめに
みなさんこんにちは!
今日のテーマは「平面図形」です!今までよりも少しむずかしい問題ですが一緒に解いていきましょう!
解くために知っておかないといけないポイントが1つありますので、それをまずは勉強していきます!
いつも通り、ヒントからていねいに説明しますね!
黄色い三角形は赤い三角形の何倍か?
まずは図形の基本について勉強しましょう。
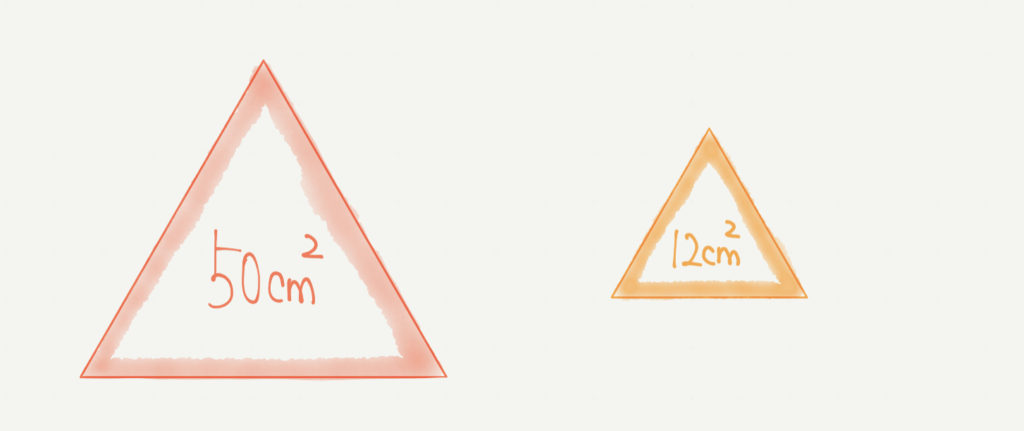
ここに赤と黄色の2つの三角形があるとします。
それぞれの面積は赤が50㎠で黄色が12㎠です。
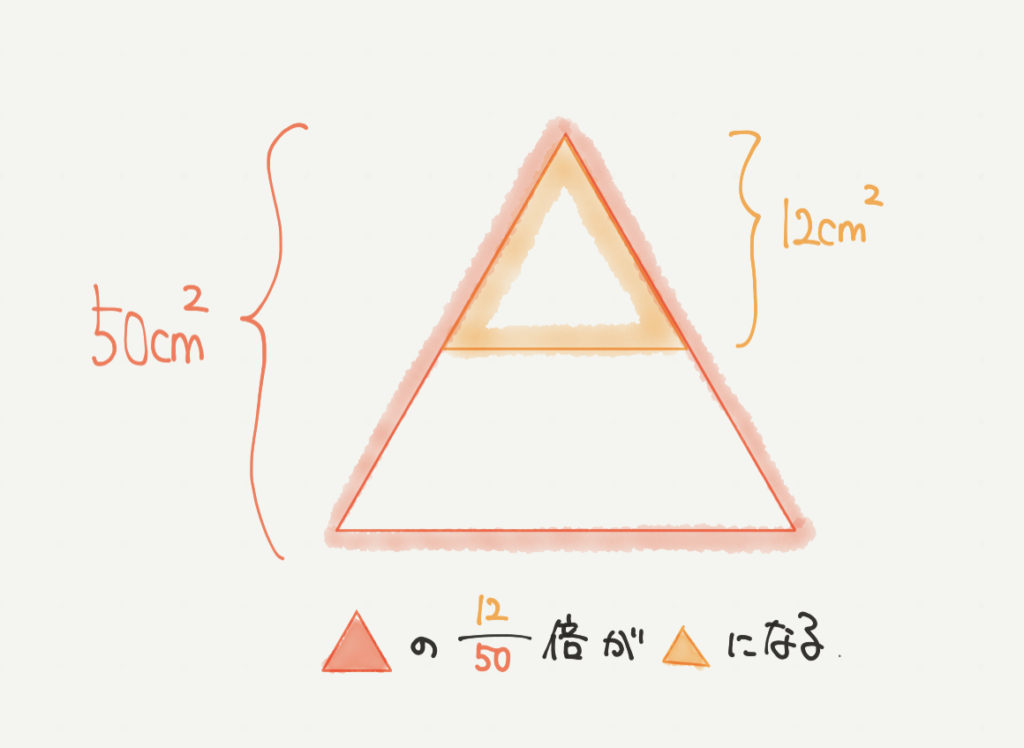
このとき▲:▲の面積比は50㎠:12㎠で25:6となります。
そして上の図を見てわかるように、▲の面積の12/50倍が▲になるとわかると思います。
↑わかりやすくするためにあえて約分せずに書いています。
ちなみに▲の50/12倍が▲とも書くことができます。
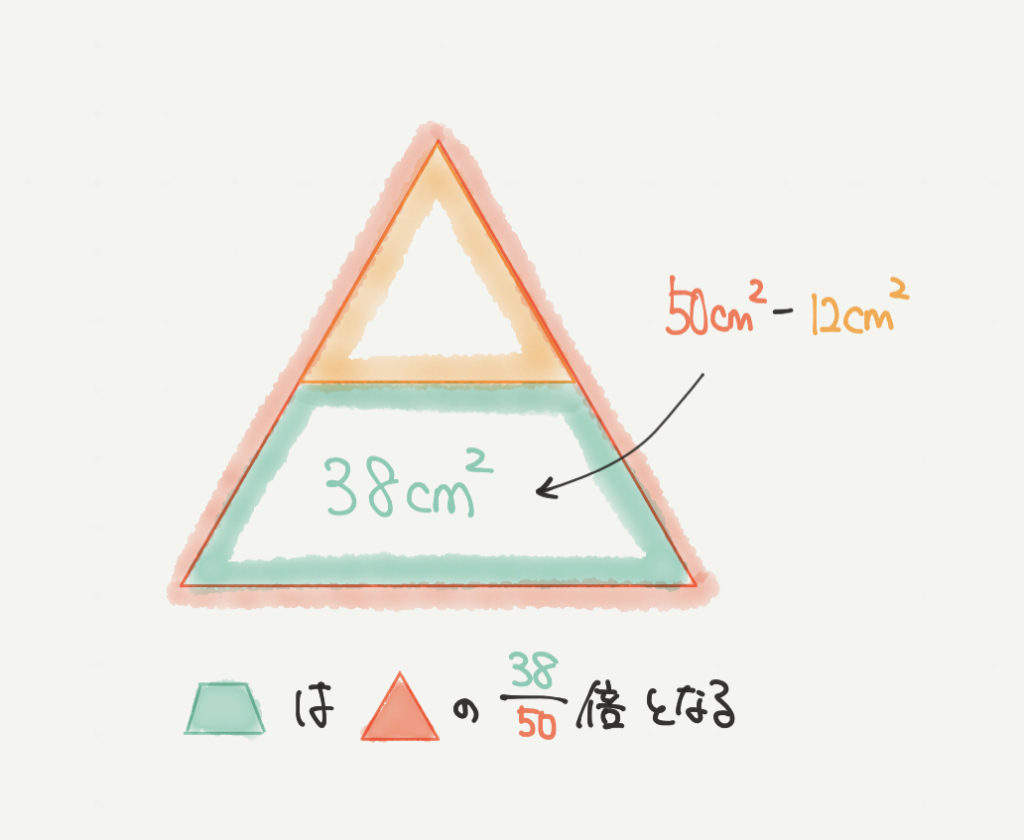
ちなみに、緑の四角形の部分は38㎠になります。
これは▲–▲=38㎠だからだね!!
その通りです。なので同じように、■は▲の38/50倍の大きさであることがわかると思います。
ただ、ここまで理解できても、実はまだ問題を解くことができません。
問題を解くために必要なもう1つのポイントをSTEP1のところで解説しようと思いますので、
まずは問題にチャレンジしていきましょう〜〜!!
問題に挑戦!
解答
答えを見るにはここをクリック!
①9/35倍
②264/7㎠
この記事を書いている人はこんな人


解説を見てみよう!
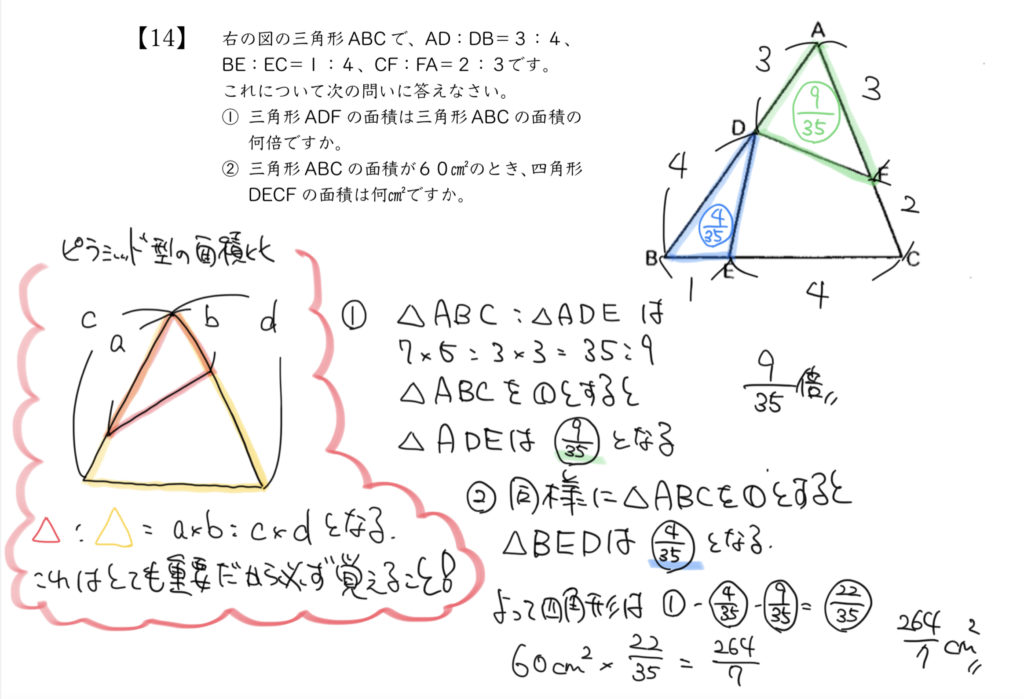
STEP1:ピラミッドの形を覚えよう
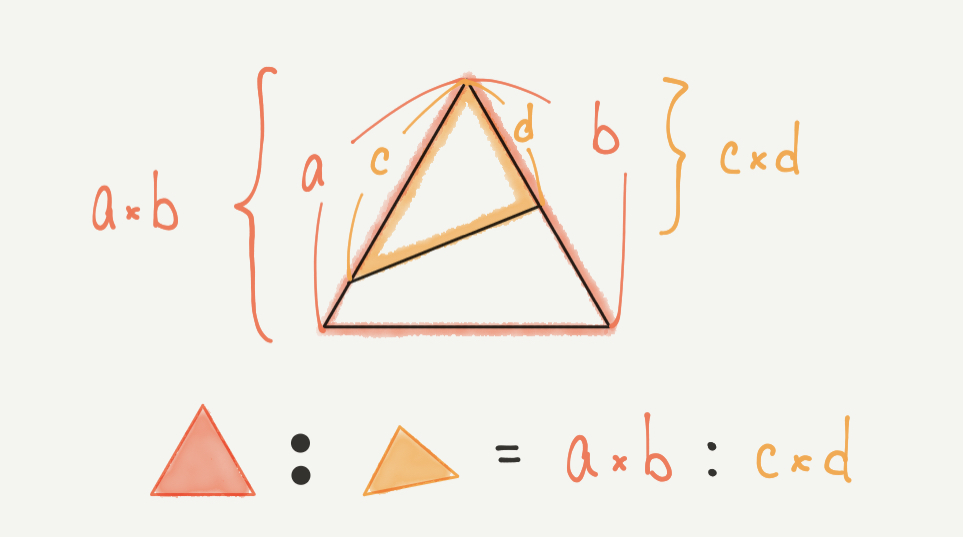
この記事で一番覚えてほしいポイントがこちらの「ピラミッドの形」になります。
三角形が2つ重なってピラミッドみたいに見えるからそう呼んでいます。
「ピラミッドの形」を使うと、ある2つの三角形の面積の比をa×b:c×dで求めることができるんです!
a,b,c,dは長さではなく、比を書いてみましょう。
具体的にどういうことかは、STEP2を見ながら考えていきましょう!
STEP2:△ADEは△ABCの何倍か求めよう
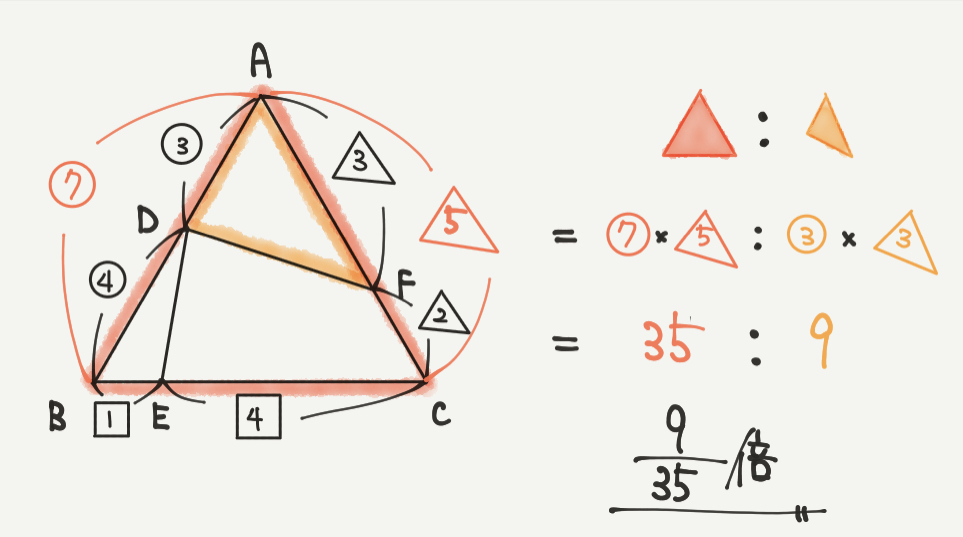
たとえば、この①の問題では△ADEと△ABCが出てきます。
問題文で書かれている比を図に書きながら考えてみましょう。
今回、聞かれている面積は△ADEなので、△ADEと△ABCで「ピラミッドの形」を見つけてみましょう。
それぞれの面積の比はSTEP1でa×b:c×dと勉強しましたので、
▲:▲
=7×5:3×3
=35:9となりました。
よって▲の面積は▲の面積の9/35倍ということがわかります!
STEP3:△DBEは△ABCの何倍か求めよう
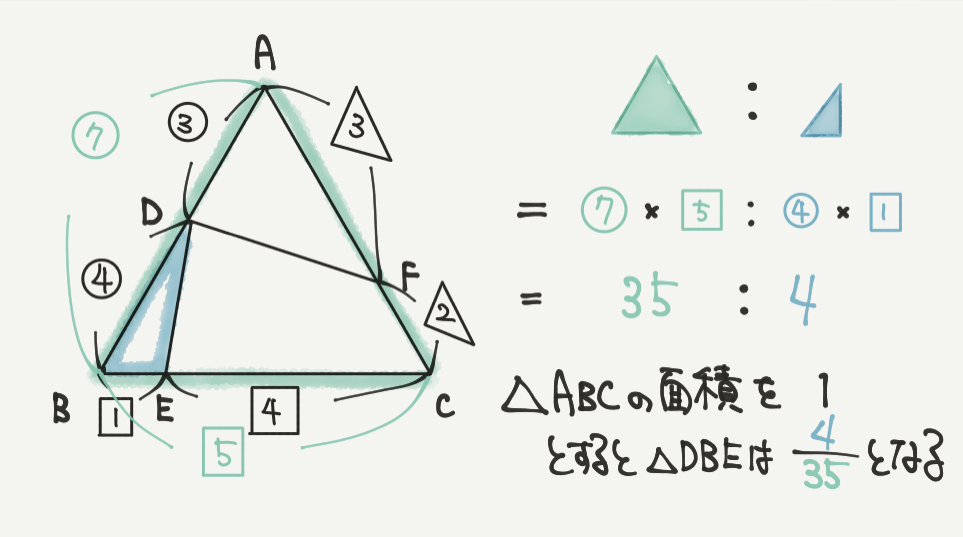
②の問題も考え方はSTEP2と同じです。
今回出てくる三角形は向きが違うので注意してください。
青い三角が左はしっこにピタッとくっついているので「ピラミッドの形」も少し向きを変えて考えます。
すると、▲:▲
=7×5:1×4
=35:4
と求められますね!
なので大きな三角形(▲=▲)の面積を1と仮定すると、△DBEは4/35と表すことができます。
↑仮定とは?「もし○○が□□だったら~」と問題を解きやすくするための考え方のことです。
今回は「もし△ABCの面積が1だったら~」と仮定しています!
STEP4:□DECFの面積を求めよう
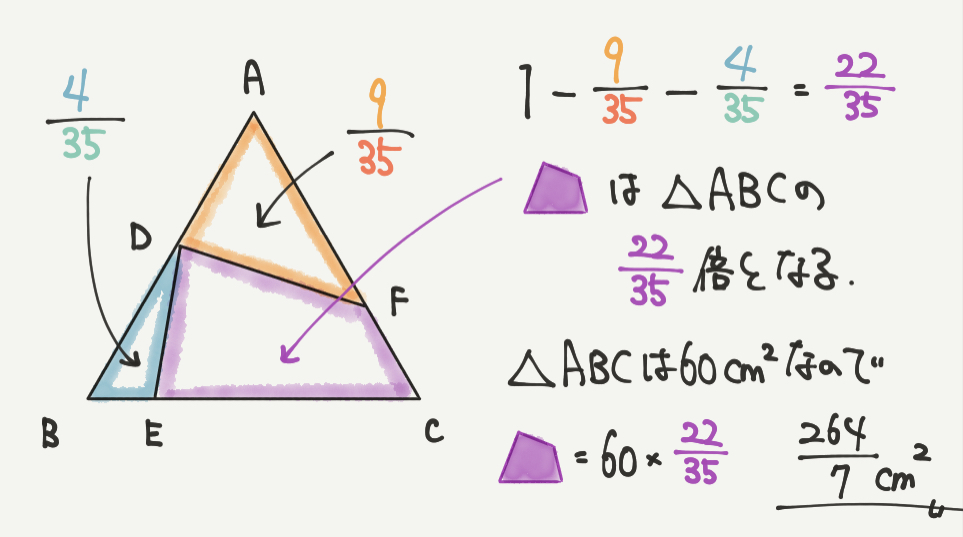
STEP2、3で△ADFと△DBEの面積がそれぞれ△ABCを1と仮定すると!
△ADF:9/35(STEP2)
△DBE:4/35(STEP3)
なので、紫の四角形は全体から2つの三角形を引いていくと、
となることがわかります。
1-9/35–4/35=22/35
となります。
よって求めたい紫の面積は△ABCの22/35倍、すなわち
60㎠×22/35=264/7となることが計算できました。
これは「全体は部分と部分でできている」という算数で大切な考え方です。
この問題だと、全体(△ABC)と部分(△ADF)と部分(△BDE)と部分(□DECF)で
できていることがわかりますね!
2つの三角形の大きさを比で求める問題の解説
今回の問題で大事なポイント
- 「ピラミッドの形」の考え方(STEP1)
- 仮定の考え方(もし○○が□□だったら〜と考えること)
・今回はもし△ABCの面積が1だったら〜と仮定しました - 「全体は部分と部分でできている」考え方(STEP4)
 わかみや先生
わかみや先生今回の問題で大切だったのは「ピラミッドの形」です。
今日はこれだけしっかり覚えてください!!!!
何度も言いますが、「ピラミッドの形」の面積比は今後も重要になってくるので、
よく復習しておいてください。
少しむずかしいかもしれませんが絶対にこの後も出てくる大切な考え方なのでしっかり理解しましょう!
「ピラミッドの形」の問題はまだあまりありませんが、
それ以外の仮定の考え方の復習と「全体は部分と部分でできている」考え方は、
他の問題でもたくさん出てきています。
時間がある受験生は下の記事にも挑戦してみましょう!
仮定する考えの復習
かかった時間から速さを変えた時間を求めるには?

「全体は部分と部分でできている」考え方の復習
半円の重なった部分の面積と周りの長さを求めるには?