【中学受験攻略】算数平面図形の基本！2つの三角形の面積比をわかりやすく解説

はじめに

みなさんこんにちは！
「平面図形」の問題もいったんはこちらでおしまいです。
今までの問題で勉強したさまざまな知識を使う総まとめなので、ぜひ気を引き締しめてください！

今までに勉強した内容だと、「仮定する考え方」「同じところを作る考え方」
「補助線」「相似」「等積変形」などなど、たくさんありましたね！

これらの考え方の一部を使って、4つの問題にチャレンジしていきましょう。
その前にいつも通り今回の問題を解くために必要なヒントについてかんたんにおさらいしておきましょう。

高さが同じとき三角形の面積比は底辺の比と等しい

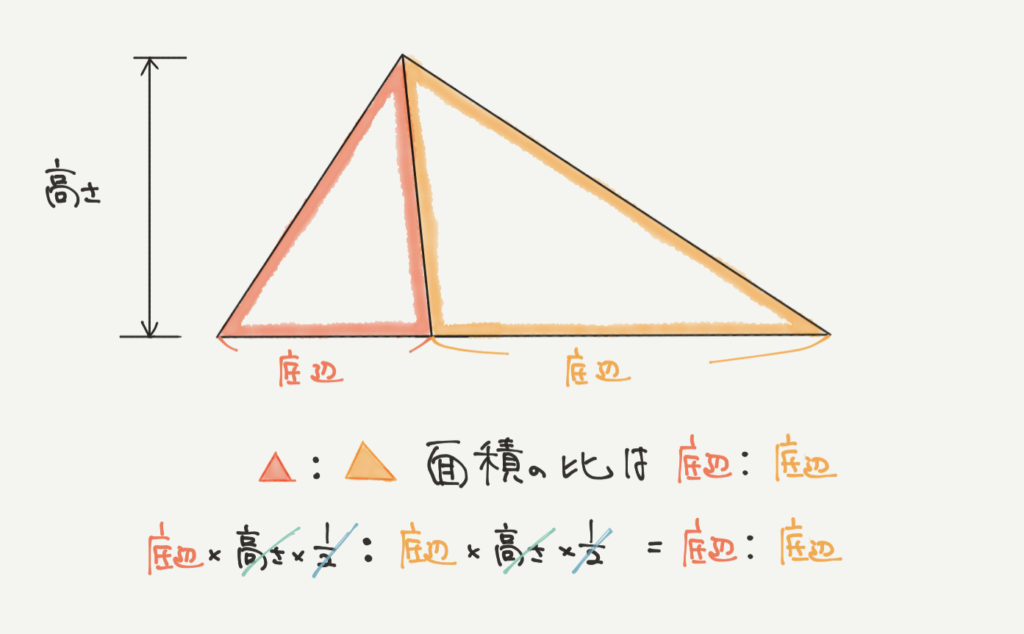
まずは高さが同じときの三角形の面積比を計算してみましょう。
三角形の面積は「底辺×高さ×1/2」でしたので、赤と黄色の三角形のぞれぞれの面積は

赤：底辺×高さ×1/2
黄：底辺×高さ×1/2
となりますね。

なのでこの2つの面積比は
赤：黄
＝底辺×高さ×1/2：底辺×高さ×1/2
＝底辺：底辺

となることがわかります。

ピラミッドの形の復習

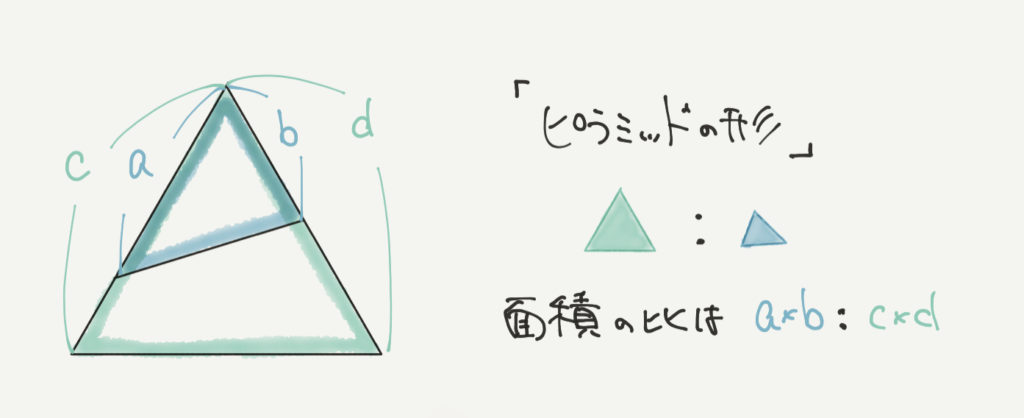
続いては三角形が2個こ重なっているような図形について見ていきましょう。

このピラミッドみたいな図形のとき、緑と青の三角形の面積の比は

青：緑
＝a×b：c×d

となります。

これはどうしてこうなるのか？と考えるとむずかしくなってしまうので、
いったんは公式のように覚えてもらえるといいと思います。

ちなみにaとかb、c、dとかには実際の数字が入ったり、比の数字が入ったりします。
詳しくは解説のSTEP2を見てみてくださいね。

それでは問題を見ていきましょう！！

問題に挑戦ちょうせん！

次の①〜④のそれぞれの図で、アの三角形とイの三角形の面積の比を求めなさい。

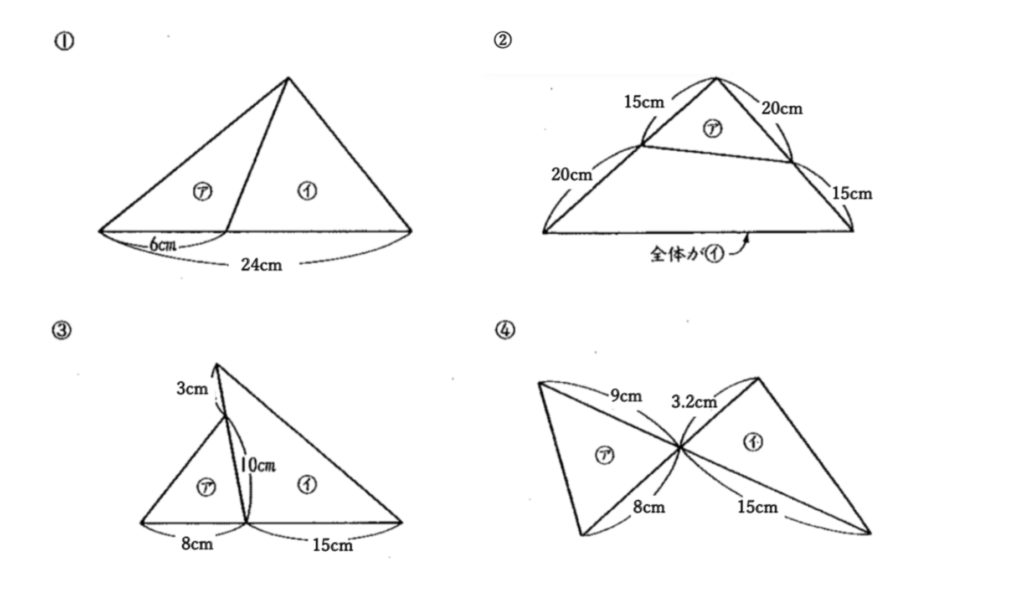
解答

この記事を書いている人はこんな人

解説を見てみよう！

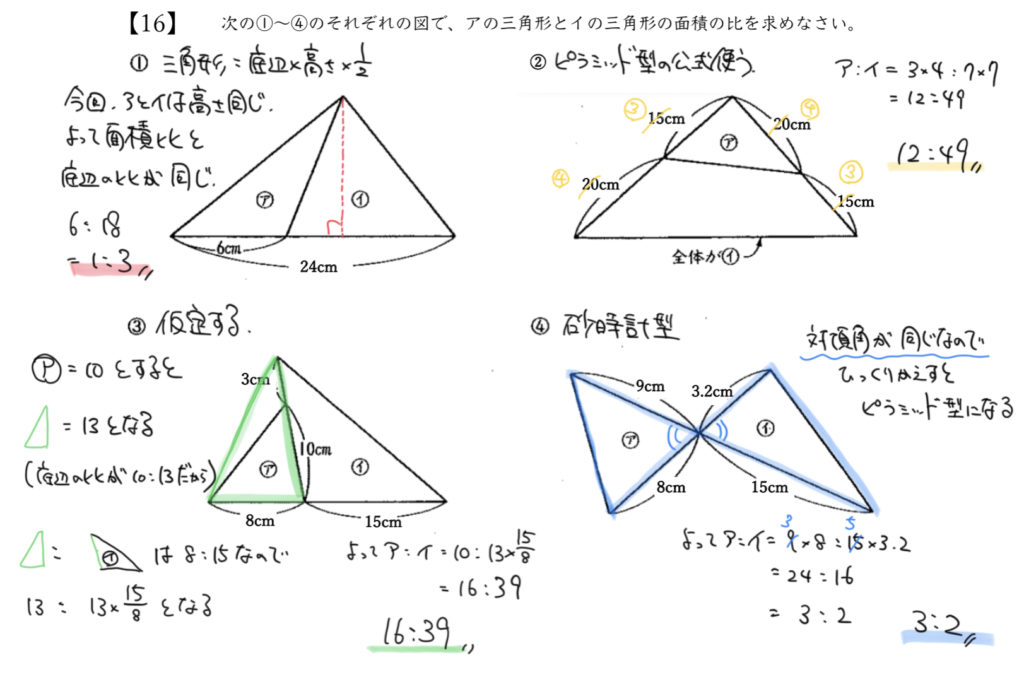
STEP1：三角形の比は底辺：底辺で求められる

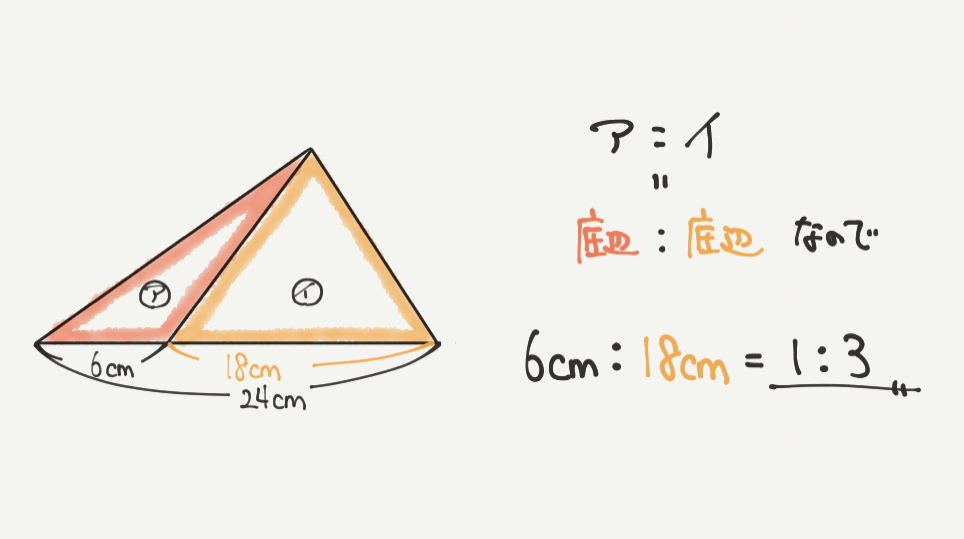
赤と黄色、どちらの三角形も底辺が違ちがうだけで、高さは同じです。

よって、はじめにで勉強した通り三角形の面積比は底辺の比と同じになります。

今回24cmと6cmがわかっているので、イの底辺の長さは18cmとわかります。

よって面積比は6cm:18cm=1:3になります。

STEP2：ピラミッドの形を使おう

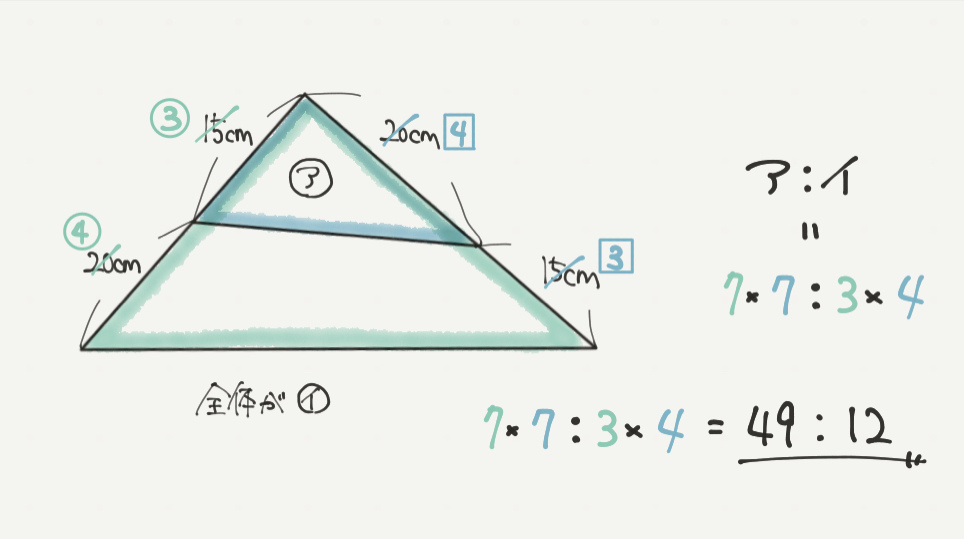
②の問題はそのまんまピラミッドの形をしていますね！

こちらもピラミッドの形の公式を使います。

実際の数字を使って比を出すと数が大きくなってしまうので、それぞれの辺を比で表してみましょう。

今回は全部の辺が同じ5という数で割れるので解くことができますが、
比を出すときは緑と青で必ず別で比を出すようにしましょう。

よってピラミッドの式に当てはめて計算すると、

ア:イ
＝7×7:3×4
＝49:12

となりました！

STEP3：補助線と仮定の考え方を使おう

STEP3.1：▲は▲の何倍か考えよう

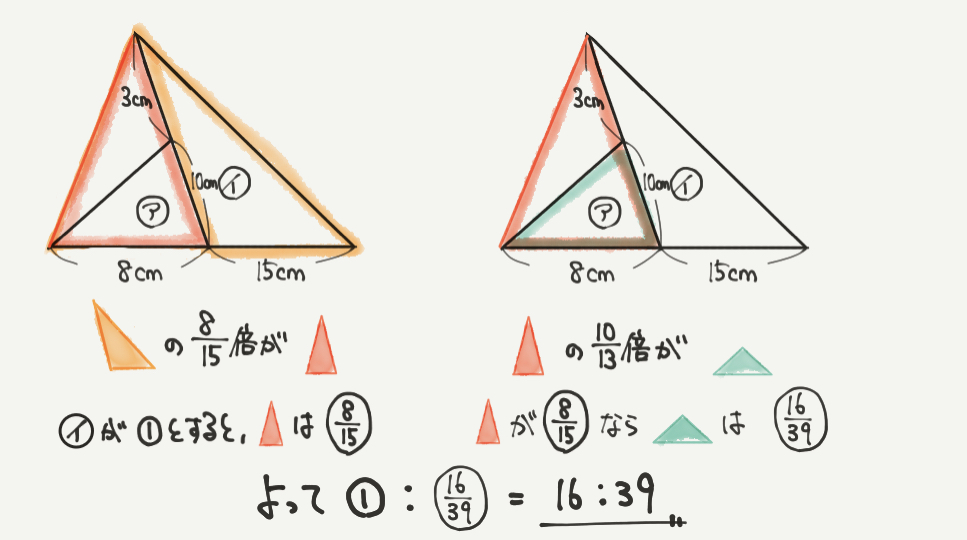
左の図を見てみましょう。赤い補助線を引いてSTEP1の問題と同じような形に直しました。

すると高さが同じになるので、▲と▲の面積の比が8:15になることがわかります。

よって▲は▲の8/15倍になるということです！

STEP3.2：▲は▲の何倍か考えよう

右の図を見てみましょう。

形がわかりづらいですが、これもSTEP1の形と同じであることがわかります。
赤い三角形を右にひっくり返すと、底辺が10cmと3cmで高さが同じ三角形ができますね。

▲の底辺は13cmで▲の底辺は10cmなので、
▲は▲の10/13倍ということがわかりました。

STEP3.3：イの面積を①と仮定して計算しよう

最後は「仮定する考え方」を使いましょう。
↑仮定とは？「もし○○が□□だったら～」と問題を解きやすくするための考え方のこと。
今回は「もしイの面積が①だったら～」と仮定しています！

イ（▲）の面積を①と仮定すると、▲は▲の8/15倍なので▲は○8/15となります。

そして▲は▲の10/13倍なので同じように▲は、
○8/15×10/13=○16/39と計算することができました。

求めたいア:イ＝▲:▲なので
①:○16/39=16:39が答えになります。

STEP4：図形を移動させてピラミッドの形にしよう

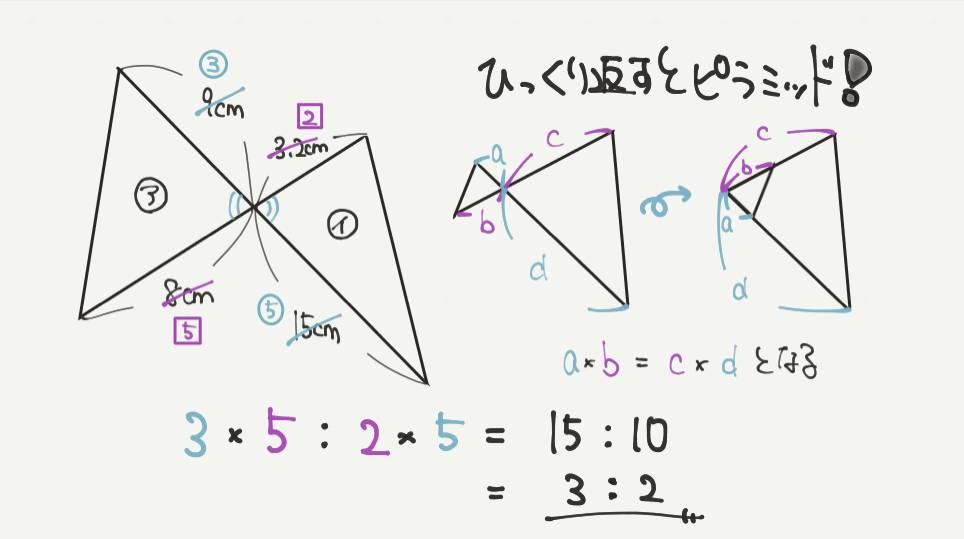
最後は④の問題！こちらはピラミッドの形にして計算することができます。

2つの三角形の対頂角が等しいのでひっくり返すと
ピタッとピラミッドの形に変形することができます。（右の図）

なので、それぞれの長さをかんたんな比に直していけば答えが出ます。

気をつけて欲しいのは、青と紫で比を出してほしいということです。
三角形をひっくり返したときに、aとd、cとbが同じ辺上にあるので、
青と紫で比を出さないと答えが計算できなくなってしまいます。

すると、
9cm:15cm=3:5
8cm:3.2cm=5:2

になるので、2つの三角形の面積の比は
3×5:5×2
=15:10
=3:2

と求めることができました。

2つの三角形の面積比を求める問題のまとめ

今回の問題で大事なポイント

• 高さが同じときの三角形の面積比の考え方（はじめに、STEP1、3）
  ・高さが同じとき、三角形の面積比は底辺の比と同じになる！
• ピラミッドの形（STEP2、4）
• 補助線の考え方（STEP3）
• 仮定する考え方（STEP3）

以上が三角形の面積比を求める問題でした！！
全4問と盛もりだくさんでしたが正解することはできたでしょうか？？？

今回の問題ははじめにでも説明した通り、平面図形で大切な考え方をたくさん使う問題たちでした。

それぞれの問題で知っておかないといけない知識が少し違ちがうので、
自分がどこで間違まちがえたのかを理解して復習するようにしましょう。

ピラミッドの形を使う問題の復習

2つの三角形の大きさを比で求めるには？

補助線の考え方を使う問題の復習

２種類の大きさの箱にみかんを詰つめ合わせるには？

仮定する考え方を使う問題の復習

２教科の点数の割合からそれぞれの点数を求めるには？