はじめに
さて、今回も平均算の問題にチャレンジしていきましょう。
今回の問題も平均点の考え方が出てくる問題です。
平均とはある数の真ん中を表す「だいたいこれくらい!」という数字のことでしたね。
たとえば、赤い小人が50円、黄色い小人が100円持っているとします。
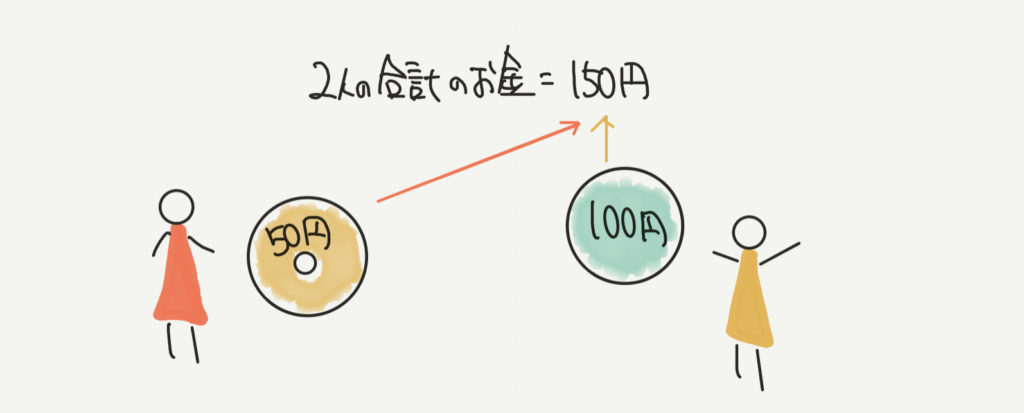
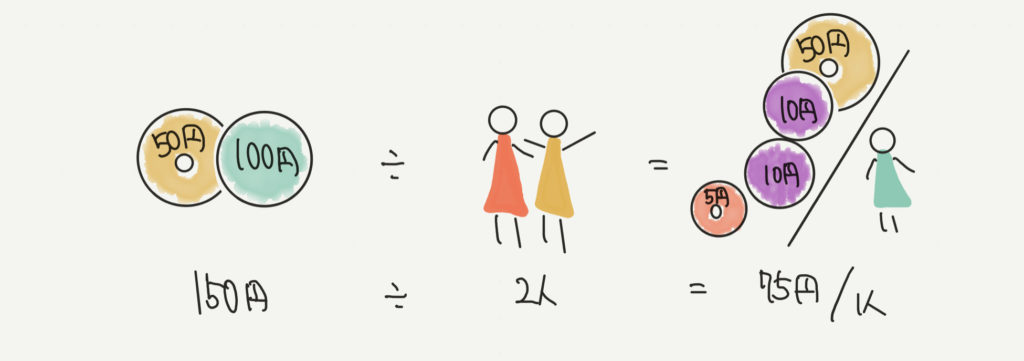
2人は合わせて 50円+100円=150円 持っていますが、
ひとりが持っているお金はだいだいいくらか考えるとき、
150円(2人が持っている合計のお金)÷2人(赤と黄の小人)=75円/1人(一人がだいたい持っているお金)
という考えで求めることができました。
平均点の問題で大事だったのは、
①面積図を書いてみること
②そこ(面積図)から同じところを見つける
という考え方を使うことの2つでした。
平均点の考え方と面積図の書き方はこちらのイラストも参考にしてみてくださいね。
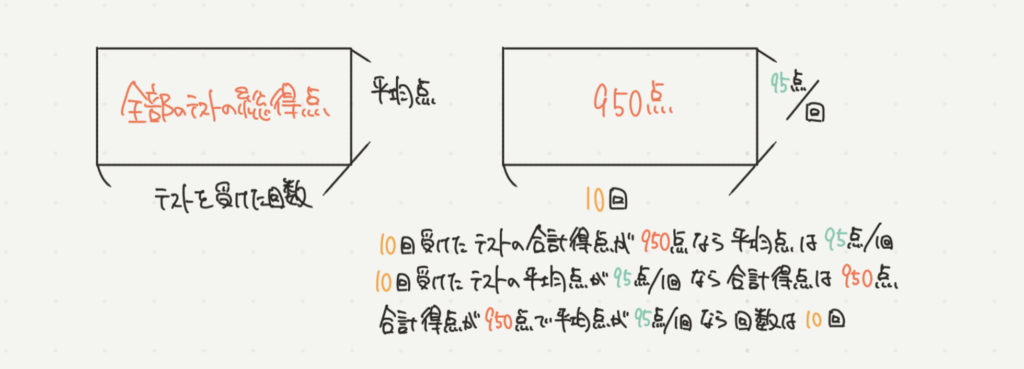
今回もその考えを使って、問題を解いていきましょう〜!
問題に挑戦!
解答
答えを見るにはここをクリック!
5回
この記事を書いている人はこんな人

解説を見てみよう!
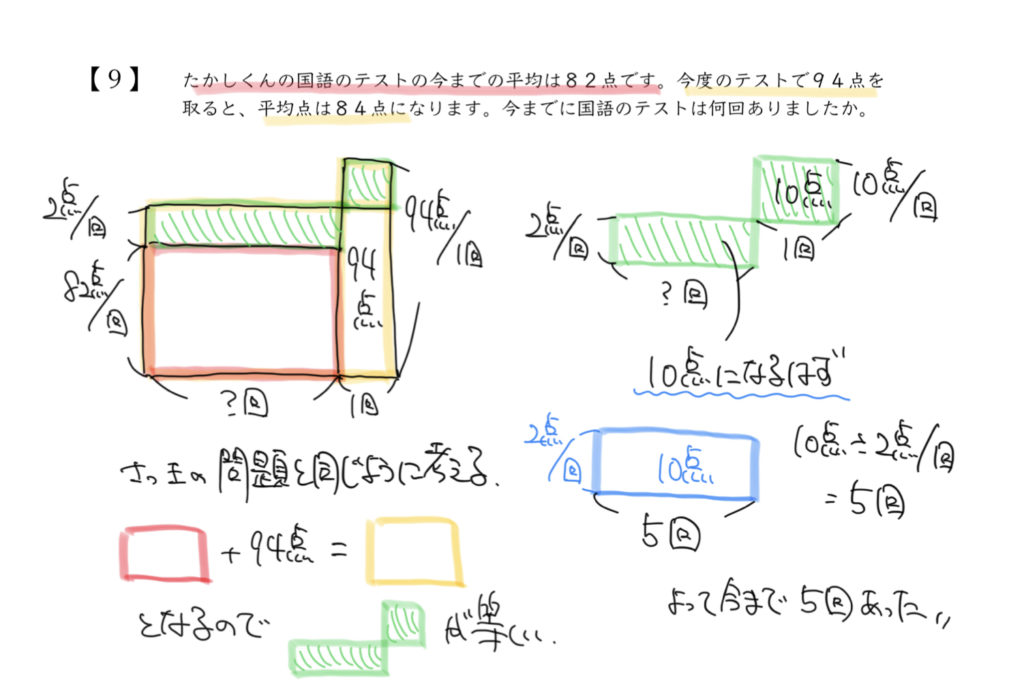
さあ、まずは問題文から面積図をかいていきます。
きちんと問題文通りに書けましたか?
解説の左側に書いてある面積図が問題文の内容をそのままかいたものになります。
横は今までにテストを受けた回数を、たては1回あたりの平均点になります。
そうなると面積(たて×横)が
1回あたりの平均点(たて)×回数(横)=全部のテストで取った合計の点数(面積)
と考えることができます。
赤の四角形(今までのテストの合計点数)+94(今回の1回のテストの点数)
=黄色の四角(1回あたりの平均点×今まで受けたテスト)になります。
そう考えると解説の右に書いている緑の四角形2つの面積が同じになるはずなので、
緑(右)の面積が、
10点/1回(たて)×1回(横)=10点(面積)
と求めることができますので、緑(左)も10点であることがわかります。
緑(左)の面積も10点なので、
10点(面積)÷2点/1回(たて)=5回(横)となります。
同じところ(緑の面積たち)を見つけて、それらがつりあうように計算すれば答えが出ます!
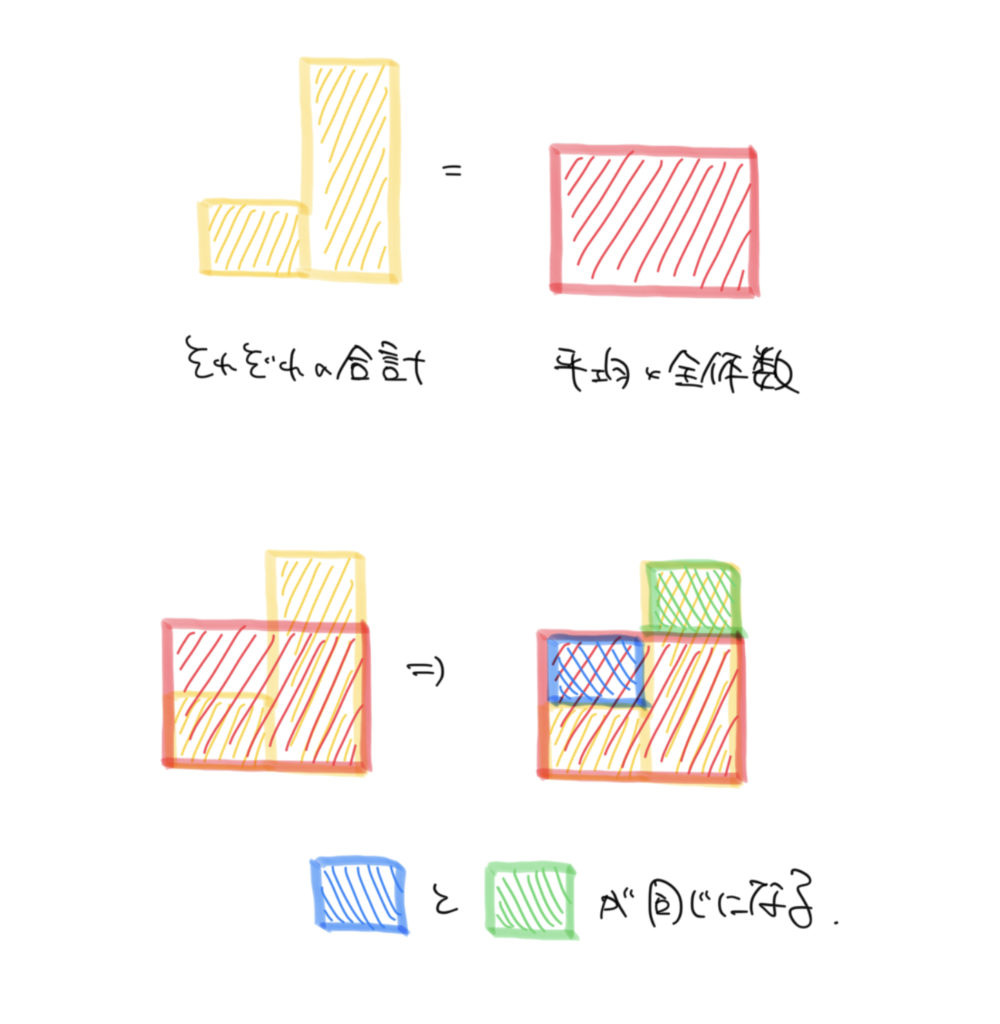
つり合いの考え方はこちらのイラストも参考にしてみてください。
 わかみや先生
わかみや先生黄色と赤色の四角形の面積が同じとき、
青色の四角形と緑色の四角形の面積が同じになります。
平均点から受けたテストの回数を求める問題のまとめ
今回の問題で大事なポイント
平均の考え方(だいたいこれくらいの数のこと)
・同じところを見つける・作る
面積図の考え方(たてと横の単位)
いかがでしたか?
平均点の問題は面積図を書いて解いてみるとかんたんに求められましたね。
この問題だけではわからない!もっと他の問題にチャレンジしたい方は他の問題も解いてみてください!