はじめに
みなさんこんばんは!
今日解く問題は「食塩水」の足し算の問題です。
「食塩水」の足し算の問題を解くためには、もちろん「食塩水」の基礎を勉強する必要があります。
もし、「食塩水」の問題に自信がない受験生がいたらこちらの記事で、「食塩水」についてとても詳しく説明しているのでお時間あるときに確認してみてください!
食塩水の問題の復習はこちらから
食塩水の濃度から混ぜた2つの食塩水を求めるには?

蒸発させる食塩水の量を求めるには?

問題に挑戦!
解答
答えを見るにはここをクリック!
225g
この記事を書いている人はこんな人


解説を読んで「 割合と比 」を攻略しよう!
STEP1:まずは問題文を図にしよう!
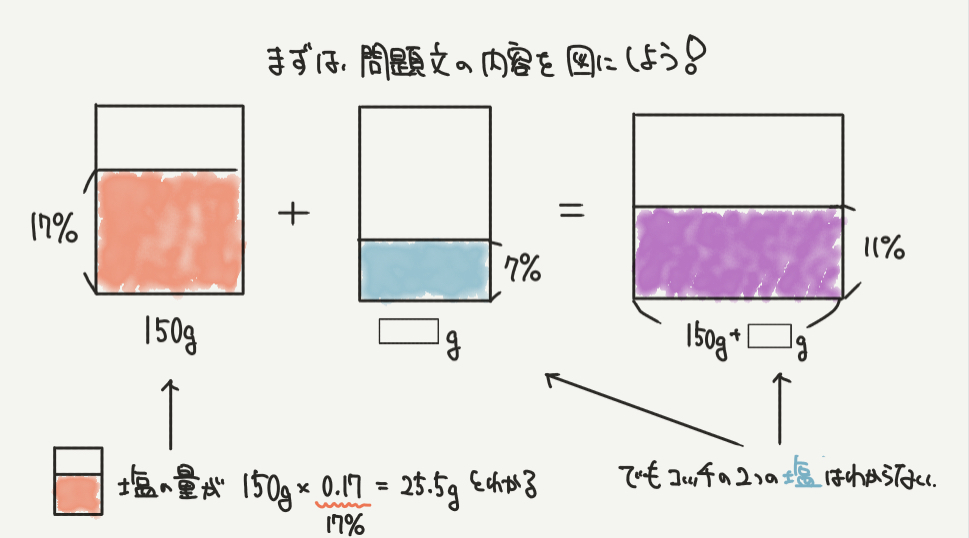
食塩水の足し算ははじめて解くとむずかしいと思うので、まずはお絵かきしてイメージを持ちましょう。
17%の食塩水150gを赤色で、7%の食塩水□gを青色で書いてみましょう。
すると、何gかはわかりませんが、紫色の食塩水11%ができあがります。
他にもわかっていることとして、赤い食塩水の塩の量が25.5gとわかりますね。
STEP2:食塩水を混ぜると、塩が移動する!
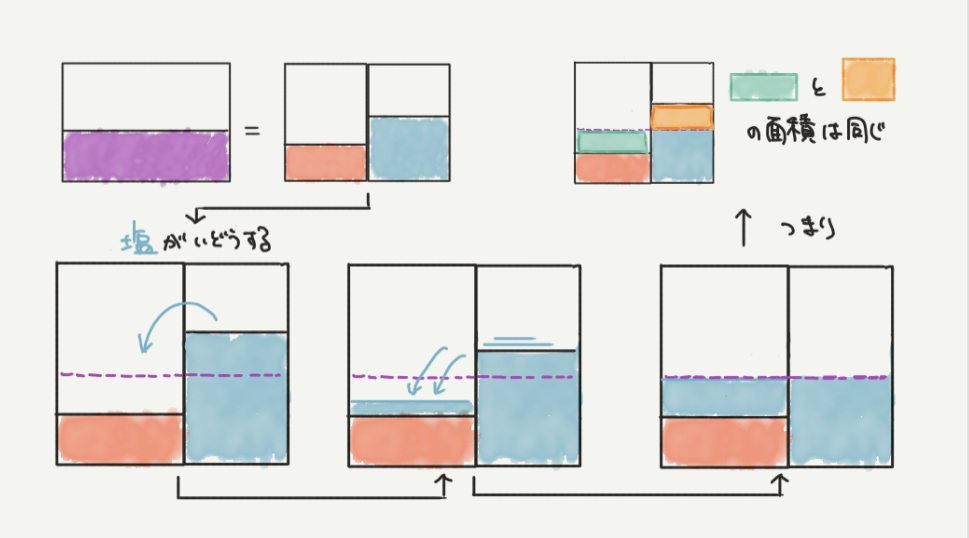
食塩水を混ぜるということは、食塩水の中の塩が一緒になる、ということです。
食塩水の絵をみながら確認してみてください。
ここでは青い食塩水の塩が赤い食塩水よりも多いので、青の塩が赤い食塩水に移動します。
そこで塩の量が均一になるので、濃度が11%の食塩水ができることになります。
STEP3:同じところを見つける作る!
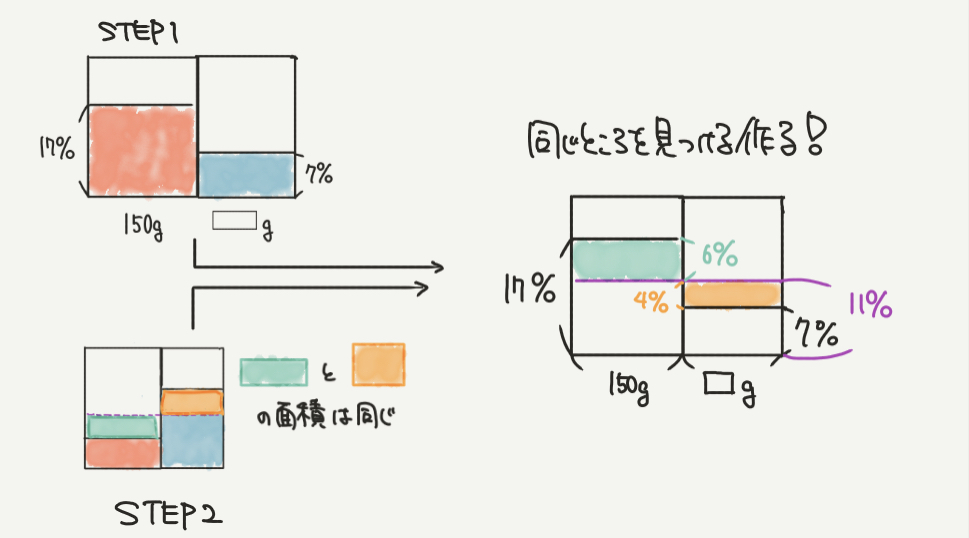
STEP2の内容を理解すると、今回の問題では赤い17%の食塩水の塩が
青い7%の食塩水に移動したことが図からわかります。
そして移動した塩の面積(量)は同じになるはずなので、
緑と黄色の四角形の面積が同じになります。
これが「同じところを見つける、作る」という考え方です!
2つの四角形のたての長さは17%、11%、7%を使って、
17%−11%=6%
11%−7%=4%
と計算できます。
ここまで計算できたらあとはもう少しです!!
STEP4:最後は逆比を使って計算しよう!
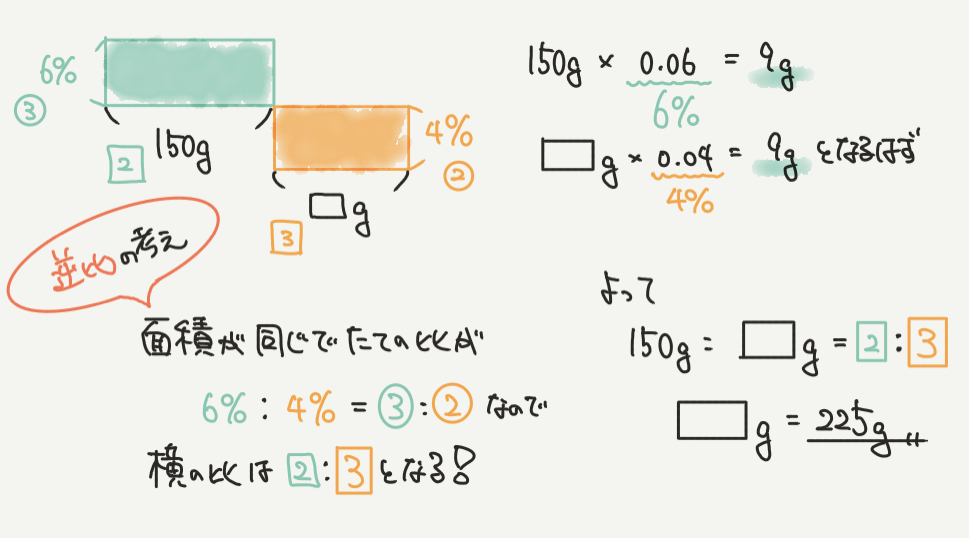
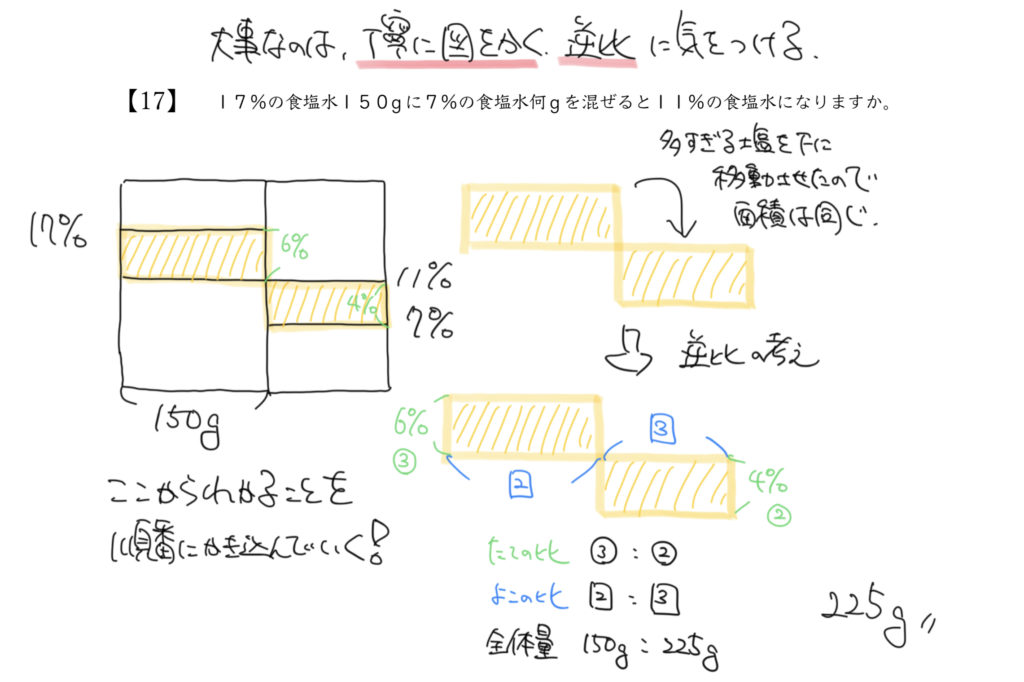
面積が同じ四角形で、たての比が6%:4%=3:2です。
これを逆比の考えを使って解いていきます。
面積が同じなので、横の比は2:3になります。
よって150g:□g=2:3となりますので、
□g=225gとなりました。
↑150g=2なので、□g=(150g×3)÷2で225gとなります。
逆比を使わない解き方
ちなみに逆比を使わなくても解けます!(時間がかかるやり方なのでおすすめしません!)
解説の図の右上に書いていますが、塩の量が9gとわかっているので、
黄色の四角形の面積を出すやり方でも□g=225gとわかります!!
濃度から混ぜ合わせる2つの食塩水の重さを求める問題のまとめ
今回の問題で大事なポイント
面積図の正しい書き方(足し算は面積図をつなげてかこう!)
逆比の考え方(面積が同じとき、たての比と横の比が反対になる)
平均の考え方(平均は「だいたいこれくらいの数」という考え)
食塩水の考え方(食塩水の復習は前の記事から!)
少しむずかしかったと思いますが、理解できましたか?
ていねいに解説を書きましたが、それでもわからない受験生の方がいたらぜひコメントで連絡してください!できるかぎり答えて改善していきたいと思います。
食塩水を混ぜる問題では、上の4点の考え方が大事でしたね。
1、2、3の復習は下の記事からできますのでぜひ時間をかけて、勉強してみてくださいね。
面積図の復習はこちらから↓
2種類の大きさの箱にみかんを詰め合わせるには?

逆比の復習はこちらから↓
歯車の歯数から回転数を求めるには?

平均の考え方の復習↓
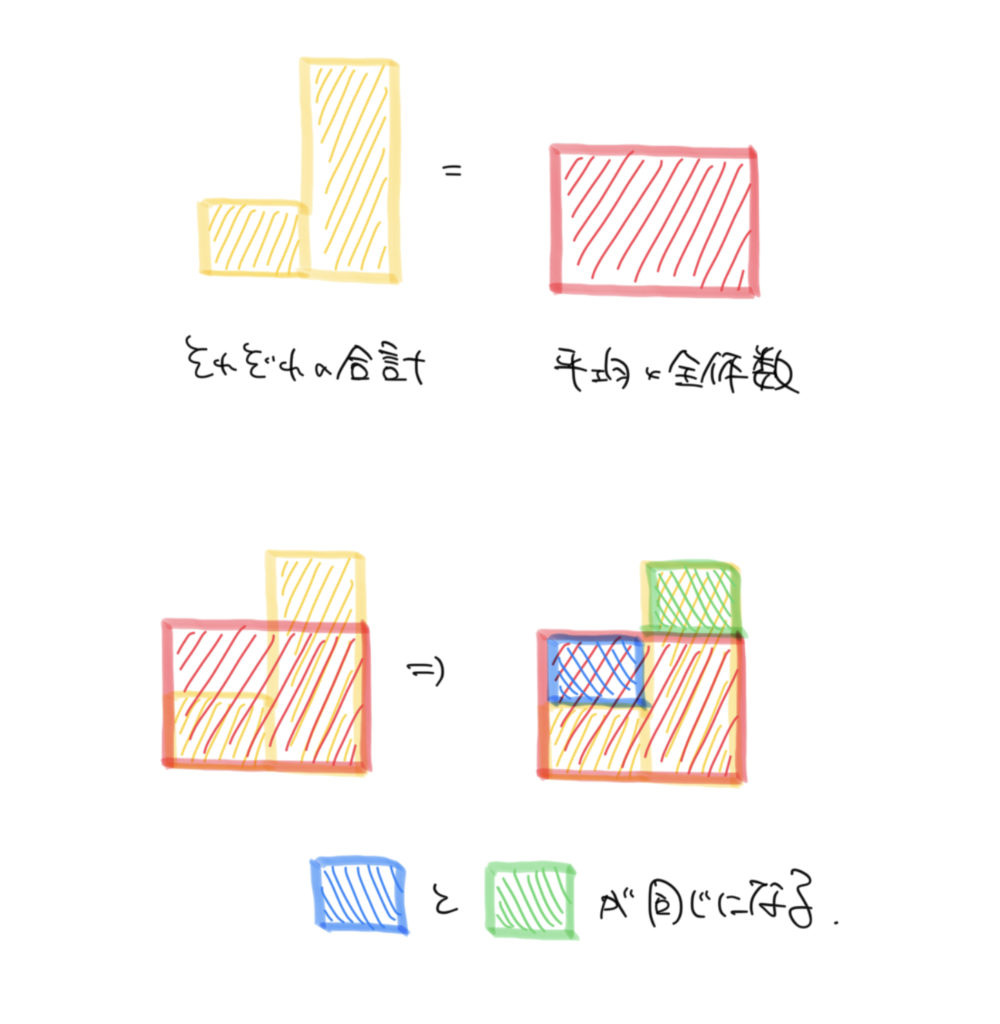
よって移動した緑の部分と増えた青の部分の面積は同じになるはず!
例えば、
めちゃめちゃ濃いカルピスとうっすいカルピスを混ぜて飲むとちょうどよくなりますよね?
でも中に入っているカルピスの原液(カルピスの元の液体)の量は変わりません。
これをふまえた上で、解説通りに解いてみてください。
男女の平均の長さから女子の平均を求めるには?