はじめに
みなさんこんばんは!!
「速さ」の問題に今日もチャレンジして行きましょう。
本日の問題も「旅人算」とよばれる問題です。
いつも通り、線分図や絵を書きながら1つずつていねいに解いていきます。
そんな「旅人算」の基本から復習しましょう。
旅人算ってなに?(復習!)
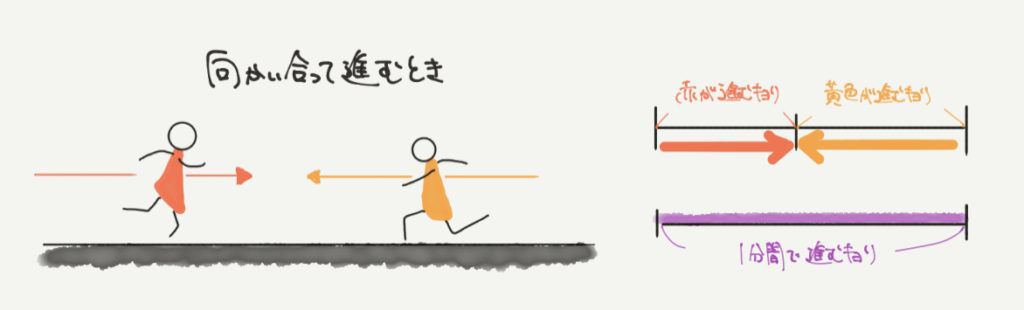
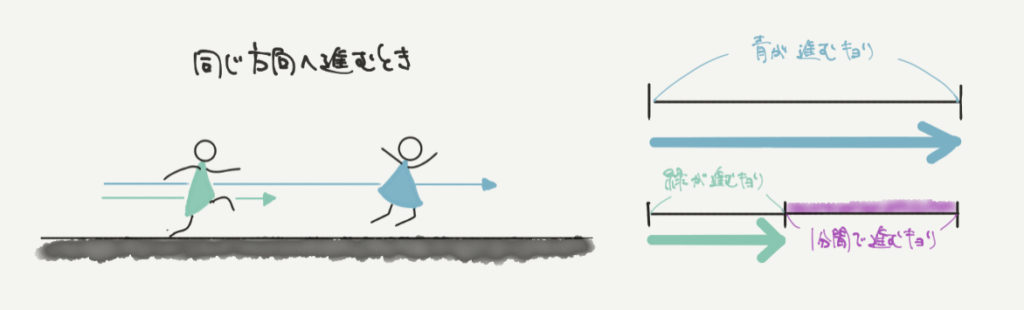
旅人算とは、違う速さで歩く人たちがいつすれ違うのか、いつ追い越されるのかを求めるような問題でしたね。
1つ前の記事では向かい合って進む問題を解いていきました。
今回はもう一つの、同じ方向を向いているパターンの問題に挑戦です!!
どこに注目すればいいのか?どうやって解いていけばいいのか?きちんと解説していますので、
一緒に頑張って行きましょう。
問題に挑戦!
解答
答えを見るにはここをクリック!
40分
この記事を書いている人はこんな人


解説を読んで「 速さ 」を攻略しよう!
STEP1:問題文の内容を図にしよう
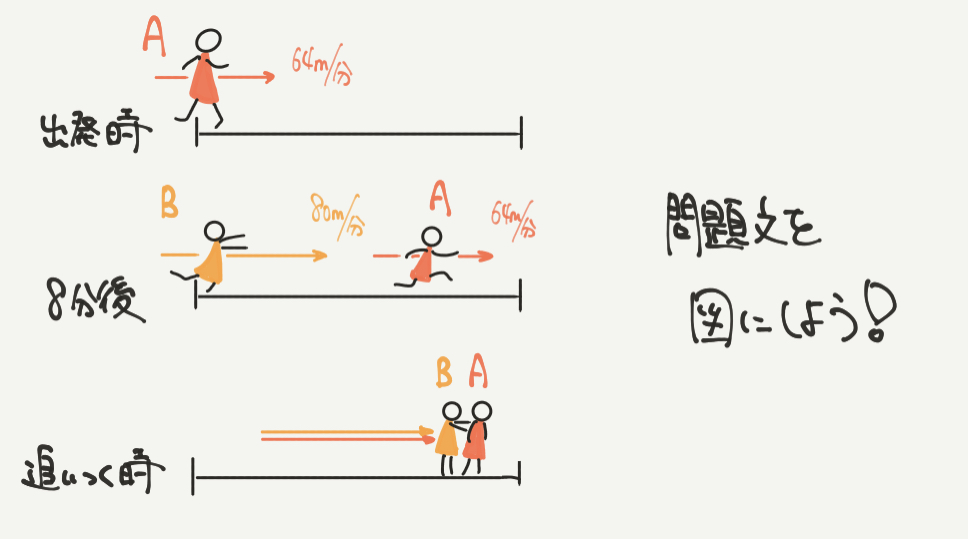
さて、まずは問題文の内容を図(絵)にしていきましょう。
まずはAさんが出発します。
8分間Aさんが走って、そのあとBさんが出発します。
そして何分後かわからないですが、2人が出会うのでその図も書いておきましょう。
算数を得意にするコツ
今まで「さんすうがく」の解説を読んできた受験生のみなさんは「あれ?単位はそろえなくていいの?」と思っているかもしれませんが、今回は速さの単位が「分」「m」だけなので、わざわざ単位をそろえる必要はありませんでした。
なのでSTEP1から問題文を図にしていきます!!
STEP2:AとBは1分間にどれだけ近づくのか?
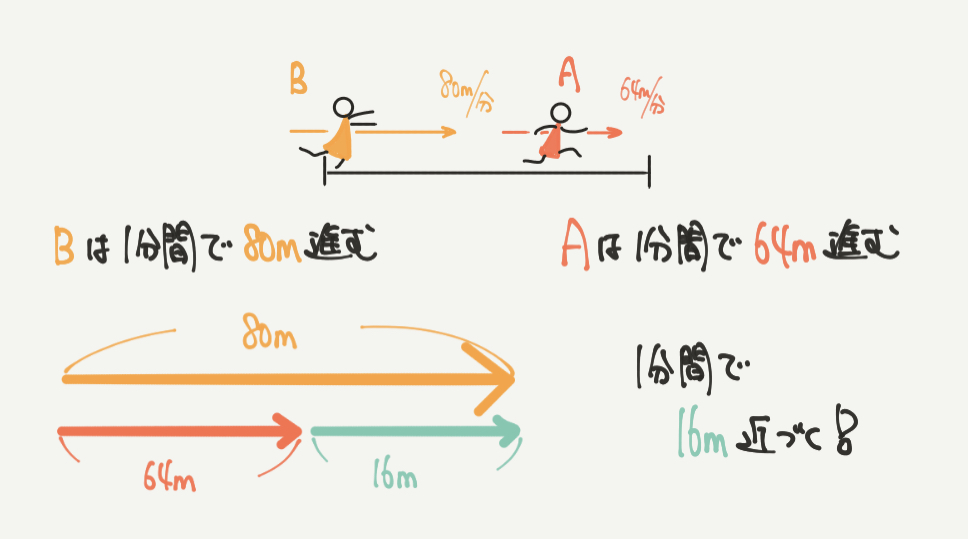
STEP1できちんと図を書くことができたら、
今度は1分でどれくらい2人の距離が近くなるのか考えていきましょう。
同じ方向に進むので、
64m/分+80m/分=144m/分ではなく!!!
80m/分–64m/分=16m/分で、毎分16mずつ近づいていくことがわかります。
STEP3:AとBはどれだけ離れているのか?
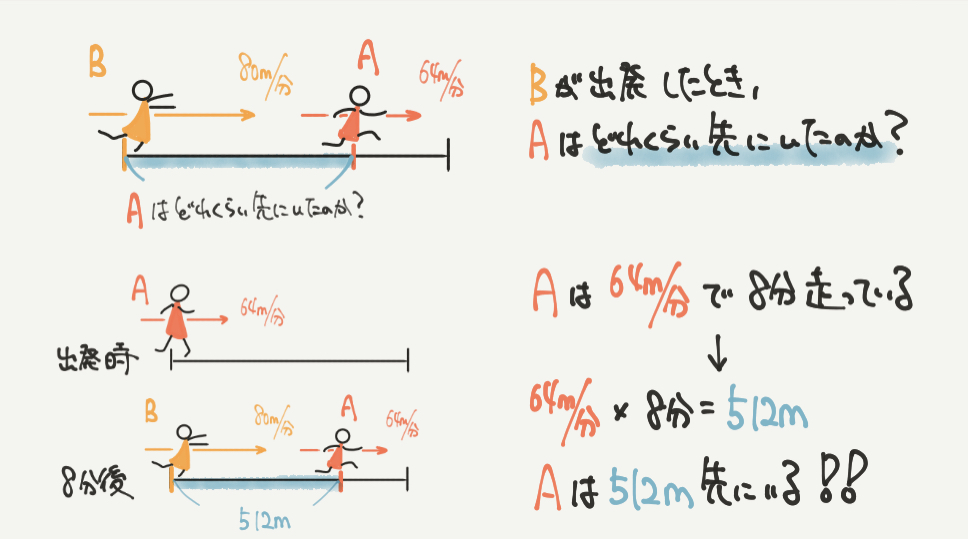
2人が1分間で16mずつ近づくことがわかりました。
あと答えを出すために知りたいのは、2人がどれくらい離れていたのか?ということです。
2人がどれくらい離れているのかは、線分図からもわかるように
Aさんが8分間で歩いた距離だけ離れていることがわかると思います。
よってAさんは8分間で、
64m/分×8分=512mということで、
AさんとBさんは始め、512m離れていることがわかります。
STEP4:出会う=2人の距離が0mになるということ
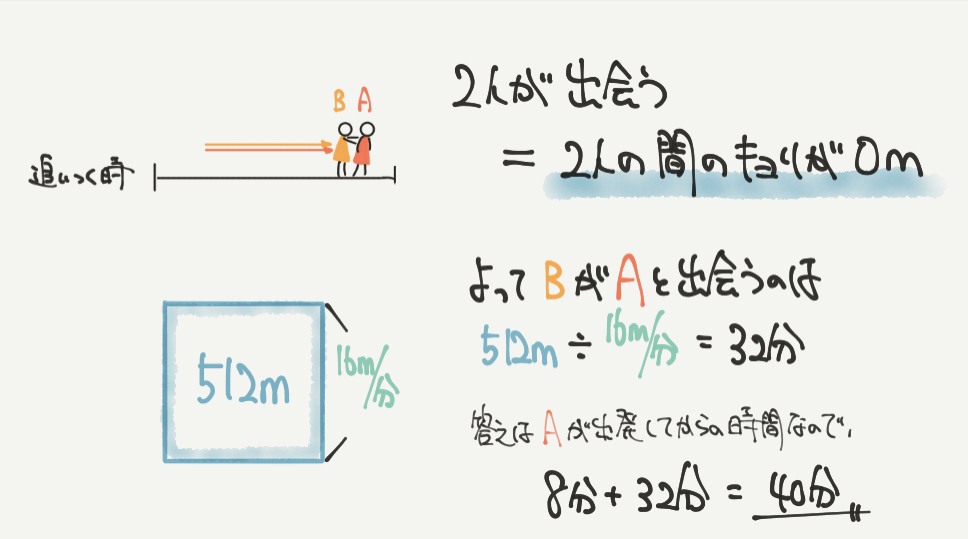
STEP3で2人は512mはなれていて、1分で80m–64m=16m近くなることがわかりました。
ここから旅人算で大切な考え方を使っていきます!!
2人は512mはなれている。(Bさん出発のとき)
2人の距離は向かい合って進むのでどんどん短くなる。(BさんがAさんを追いかけているとき)
2人の間の距離が0mになる。(出会うとき)
なので、2人が出会う=BさんがAさんに512m近づいたとき!というのがわかります。
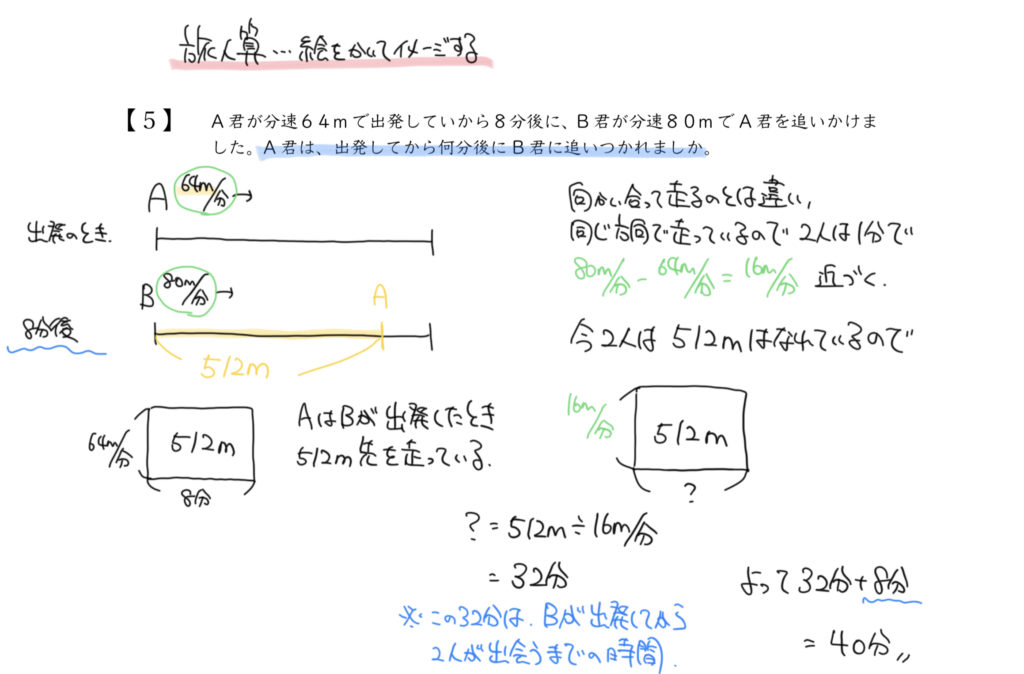
よって512m÷16m/分=32分、Bさんが出発してから32分後にBさんはAさんと出会います。
ここで32分と答えてしまうとバツになるので、きちんと何を答えないといけないのかを考えましょう。
今回の答えは、Aさんが出発してから何分後に出会うのか?でした。
なので答えは8分(Aさんが先に走っていた時間)+32分(BさんがAさんに追いつくまでに走った時間)=40分となりました。
後から出発した人が追いつくまでの時間を求める問題のまとめ
今回の問題で大事なポイント
速さの単位をきちんとそろえること
同じ方向に進むときの考え方(2人の距離が1分間で短くなっていく!)
2人が出会う=2人の間の距離が0mになること!(STEP4)
今回のポイントは
①速さの単位をきちんとそろえること(今回はそろっていたので問題ないですが、必ず注意はしておきましょう!)
②同じ方向に向かって進むときの考え方(2人の距離が1分間でどれだけ短くなっていくのか?)
③2人が出会う=2人の間の距離が0mになること!
の3点でしたね。
向かい合って進む問題と、セットに勉強しておくと頭にスッと入ってくると思います。
ぜひ下の記事から復習してみてください〜。
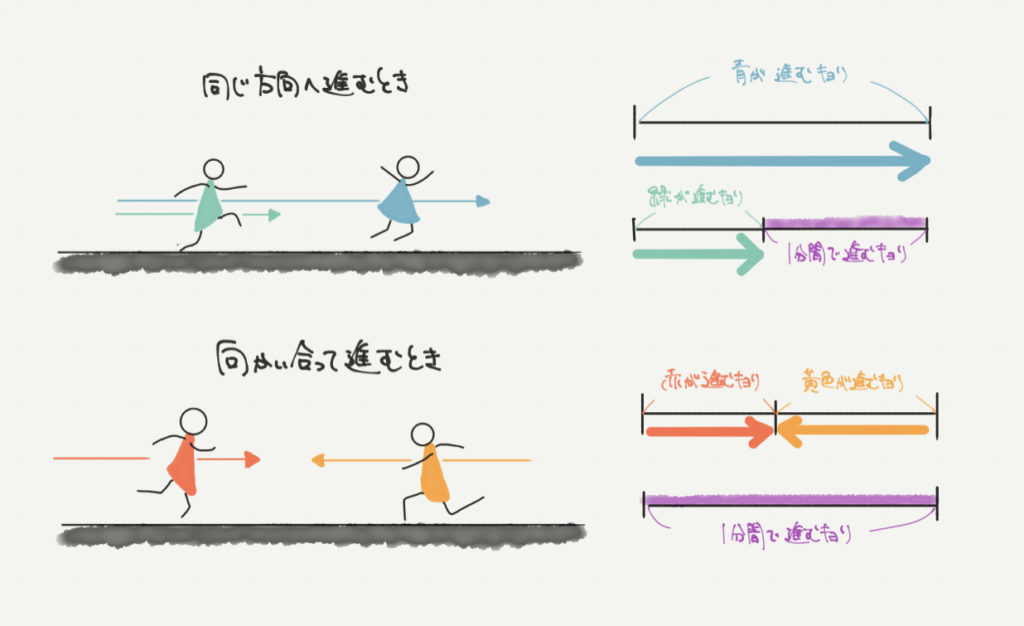
向かい合って進む旅人算の問題の復習
2人が向かい合って進むときのすれ違う時間を求めるには?