【中学受験算数】旅人算の復習！向かい合う2人が2回目にすれ違う時間を求めるには？

はじめに

おはようございます！！
「速さ」の問題に今日も挑戦ちょうせんです。

今まで「さんすうがく」で解いてきた「旅人算たびびとざん」の問題と比べると少しむずかしい問題になっております。
まずは基本的なところから考えてみましょう！

旅人算たびびとざんの復習

1分間にどれだけ距離が近づくかを考えよう！

旅人算で大切な考え方の1つは、1分間で（または1時間で）どれくらいの距離きょりが変わるのか？をきちんと考えることです。

同じ方向に進むときの考え方

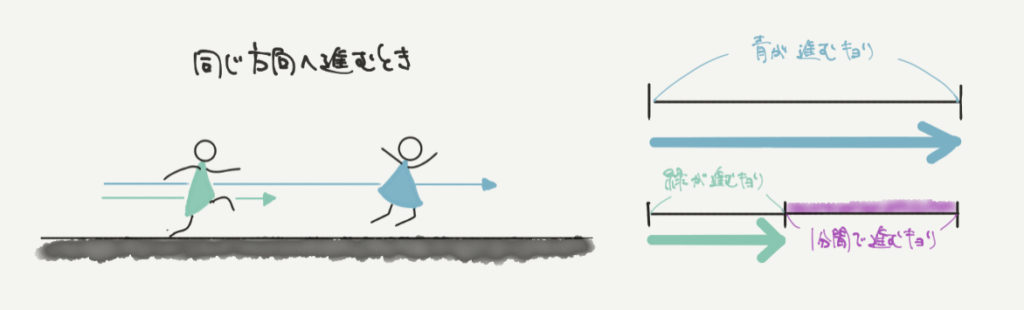
同じ方向に進むとき、青い小人が進んだ距離きょりから、緑の小人が進んだ距離きょりを引いたものが1分間に近づく距離きょりということがわかります！

例たとえば、青が毎分100m、緑が毎分40mの速さで同じ方向に進むとすると、
1分間で100m-40m=60m近づくことがわかります。

向かい合って進むときの考え方

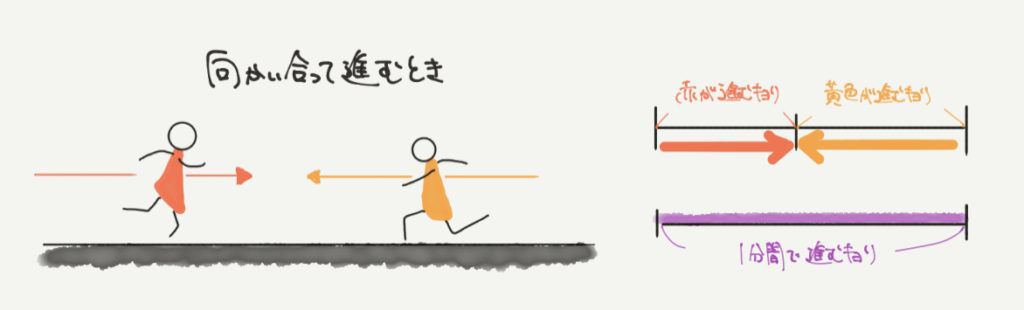
逆に向かい合って進むとき、赤い小人が進んだ距離きょり、黄色の小人が進んだ距離きょりを足したものが１分間に近づく距離きょりということがわかります！

例たとえば、赤が毎分100m、黄色が毎分30mの速さで向かい合って進むとすると、
1分間で100m+30m=130m近づくことがわかります。

出会う＝2人の間の距離が0mになること

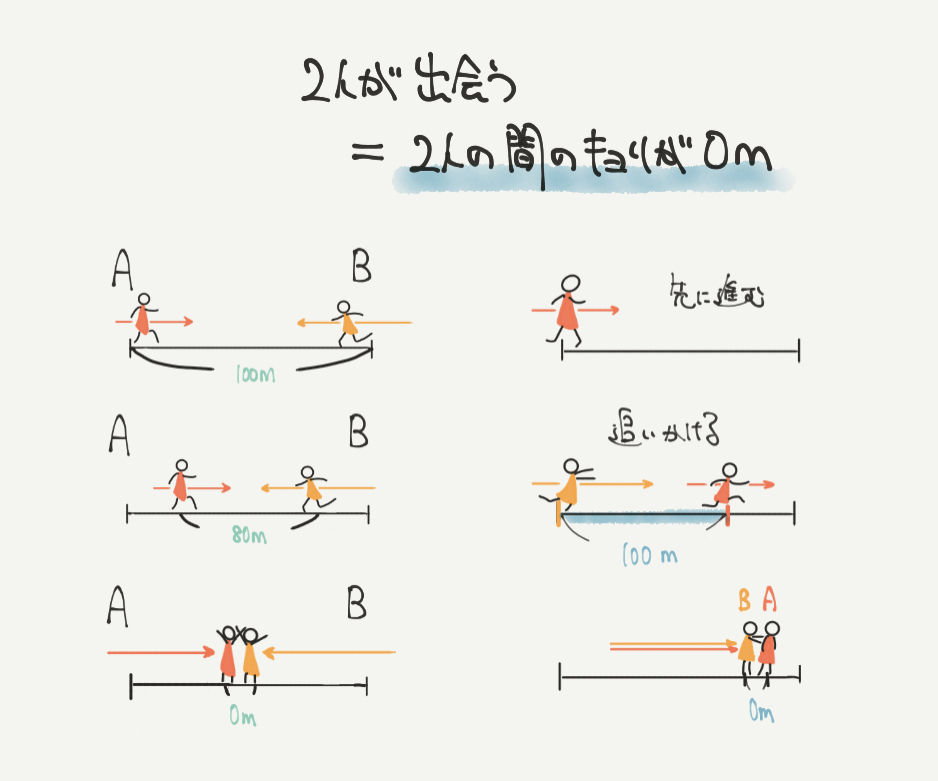
そしてもう1点大切なことがこちら！「出会うときの2人の間の距離きょりは0m」です。
向かい合って進むときも、同じ方向に向かって進むときも、2人は離はなれたところからスタートしています。
そして2人の間の距離きょりはどんどん近づいていって、最後は出会います。

このとき、線分図を見てもらってもわかるように2人の間の距離きょりは0mになることがわかりました。
この考え方も使いますので、きちんと覚えておきましょう。

問題に挑戦ちょうせん！

1.2km離はなれたA、B2地点間の距離きょりを、たかし君は分速70mでA地点から、けんとくんは分速50mでB地点から、向かい合って同時に出発し、それぞれAB間を1往復しました。
2人が2度目にすれ違うのは、出発してから何分後ですか。

解答

この記事を書いている人はこんな人

解説を読んで「 速さ 」を攻略こうりゃくしよう！

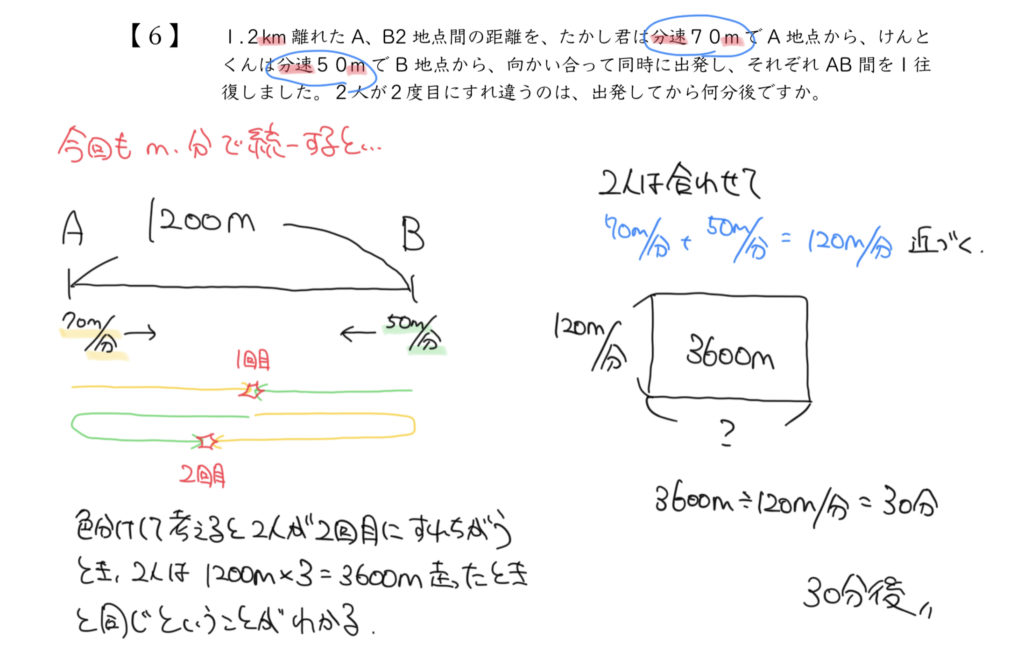
STEP1：問題文の内容を図にしてみよう

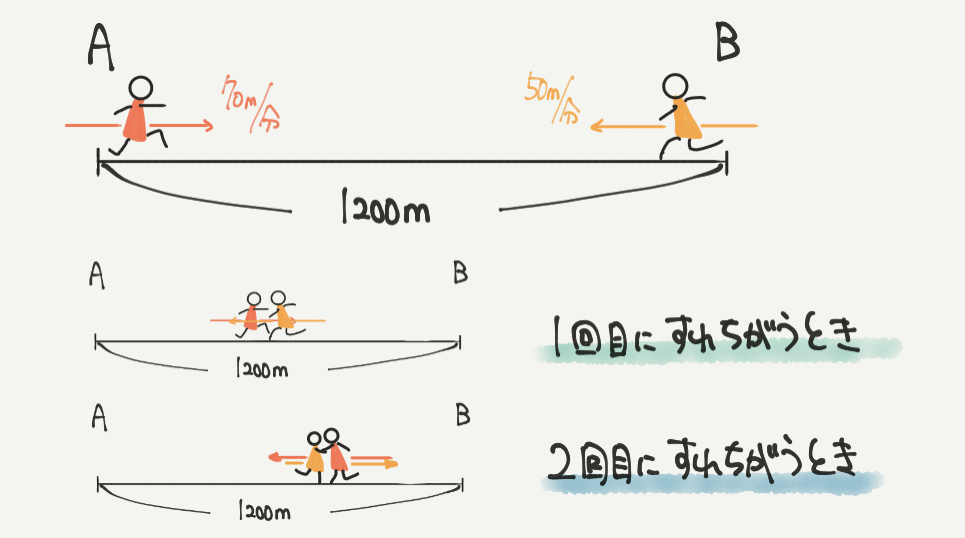
まずは問題文の内容を図に書いてみましょう。

テストや受験本番でここまでていねいに書く必要はないですが、
1人で自習しているなら時間をかけてゆっくり図を書いてみてください。

赤のたかしくんと黄色のけんとくんはそれぞれ往復するので、
1回目に出会うときと2回目に出会うときでは2人の向きが変わっています。
1回目は赤（たかしくん）が右へ向かっていて、黄色（けんとくん）は左に向かっていますね。

ただ、2回目に出会うときは赤（たかしくん）はB地点からもどってきている途中なので左に向かっており、
黄色（けんとくん）もA地点からもどってきているので右へ向かっています。

さて、ここから問題を解いていきます。

↑往復とは？行って帰ってくること。

STEP2：2人は2回出会うまでにどれだけ進むのか？

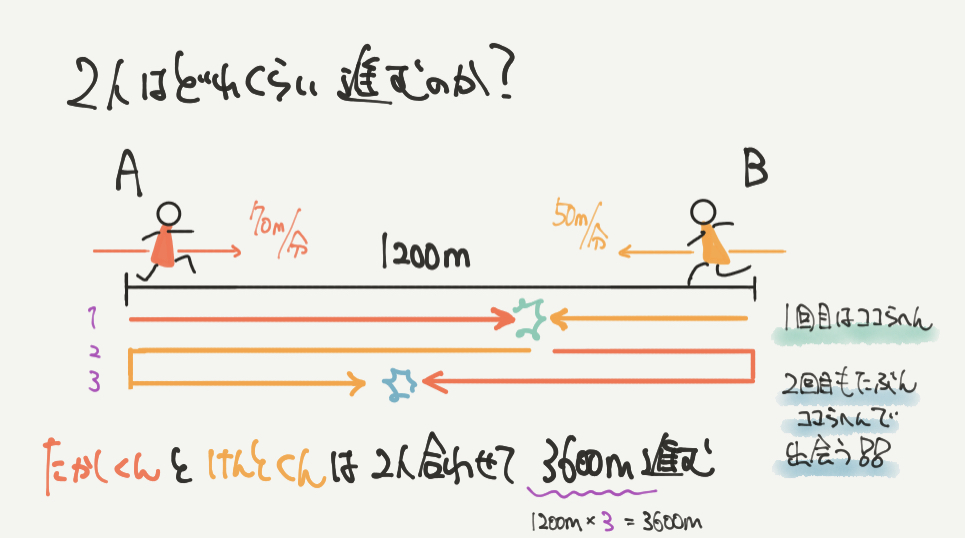
ここで2人が出会うまでに進む距離きょりを考えてみましょう。
線分図を書いていけば、2人が合わせて何m進んだのかわかりますね！

まずは1回目に2人が出会うまでに進んだ距離きょりを求もとめましょう。
こちらは解説の図にも書いてありますが、→←で合わせて1200m進んでいることになります。（図の1の部分）

そしてポイントは2回目に出会うまでに進んだ距離きょりです。
1回目に出会ってから、赤（たかしくん）は右へ向かって、BへついてからAに向かいます。

また、黄色（けんとくん）は左へ向かっていて、AについてからBに向かいます。
ですので、2人は1回目から2回目に出会うまでに、
1200m×2＝2400m、進んでいることになります。（図の2,3の部分）

よって2人が歩き始めてから2回出会うまでに進んだ距離きょりは、1200m+2400m=3600となりました。

STEP3：1回目に出会うまでの時間は何分後？

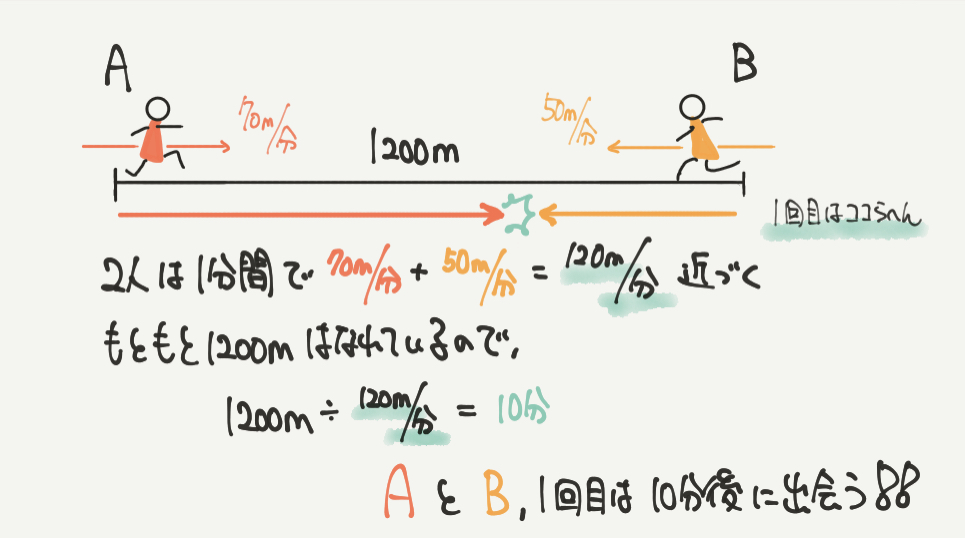
次に2人が1分間でどれくらい近づくのかを考えましょう。
赤（たかしくん）は70m/分で、黄色（けんとくん）は50m/分なので、
１分間で70m/分＋50m/分＝120m/分

1分間で120m近づくことがわかります。

よって、1回目に2人が出会うまでの時間は、
1200m÷120m/分＝10分となります。

STEP4：2回目に出会うまでの時間は何分後？

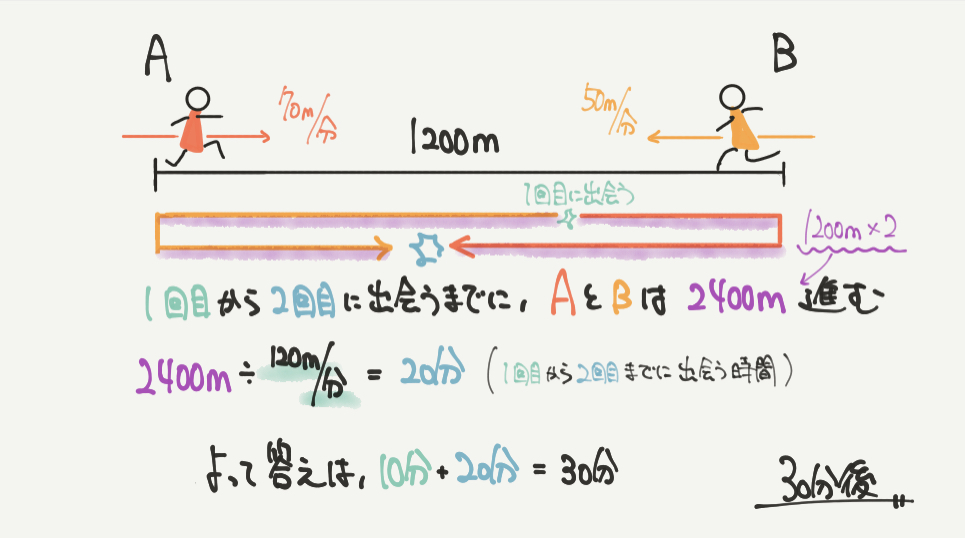
最後に1回目から2回目に出会うまでに進んだ時間を求もとめましょう。
STEP2で解説したように、2人は1回目から2回目に出会うまでに2400m進んでいます。

なので、
2400m÷120m/分＝20分

20分間かかることがわかりますね。
よって2人が進みだしてから2回目までに出会うまでの時間は

10分＋20分＝30分
30分後と答えを求めることができました。

算数を得意にするコツ

ちなみに今回の問題、STEP3とSTEP4で順番に1回目に出会う時間、2回目に出会う時間を求めましたが
この問題の答えは2回目に出会う時間だけ知りたいので、
2回出会うまでに進んだ距離きょり（3600m）÷120m/分＝30分とすぐに答えを出すことができます。

向かい合う２人が2回目にすれ違う時間を求める問題のまとめ

今回の問題で大事なポイント

往復するときの考え方（2人は行ってまた帰ってくる）
同じ方向に進むときの考え方（2人の距離きょりが1分間で短くなっていくのか？）
2人が出会う＝2人の間の距離が0mになること！

今回の問題は前回と比くらべて少し変わっていましたね。きちんと正解できたでしょうか？
あまり解かないような問題かもしれませんが、きちんと考えられればそこまでむずかしくはないと思います。

今回の問題で大事な考えである、
①往復するときの考え方（2人は行って、また帰ってくる）
②同じ方向に向かって進むときの考え方（2人の距離きょりが1分間でどれだけ短くなっていくのか？）
③2人が出会う＝2人の間の距離きょりが0mになること！
の3点でした。

これらのポイントについては下の問題でも使われる大切な考え方です。
他の速さに関する問題も下の記事きじから挑戦ちょうせんしてみてください！
今日の問題よりもかんたんなので安心してくださいね！

「旅人算たびびとざん」向かい合って進む問題のまとめ

2人が向かい合って進むときのすれ違う時間を求めるには？

「旅人算たびびとざん」同じ方向に向かって進む問題のまとめ

後から出発した人が追いつくまでの時間を求めるには？

その他の単元の問題の復習はこちらから！