はじめに
今日は「 場合の数 」の問題の10問目です!
これまで「場合の数」の問題を9問解いてきましたね!
前の問題を解きたい受験生は下の記事をクリックしてみてください!
「 場合の数 」の問題に挑戦!
解答
答えを見るにはここをクリック!
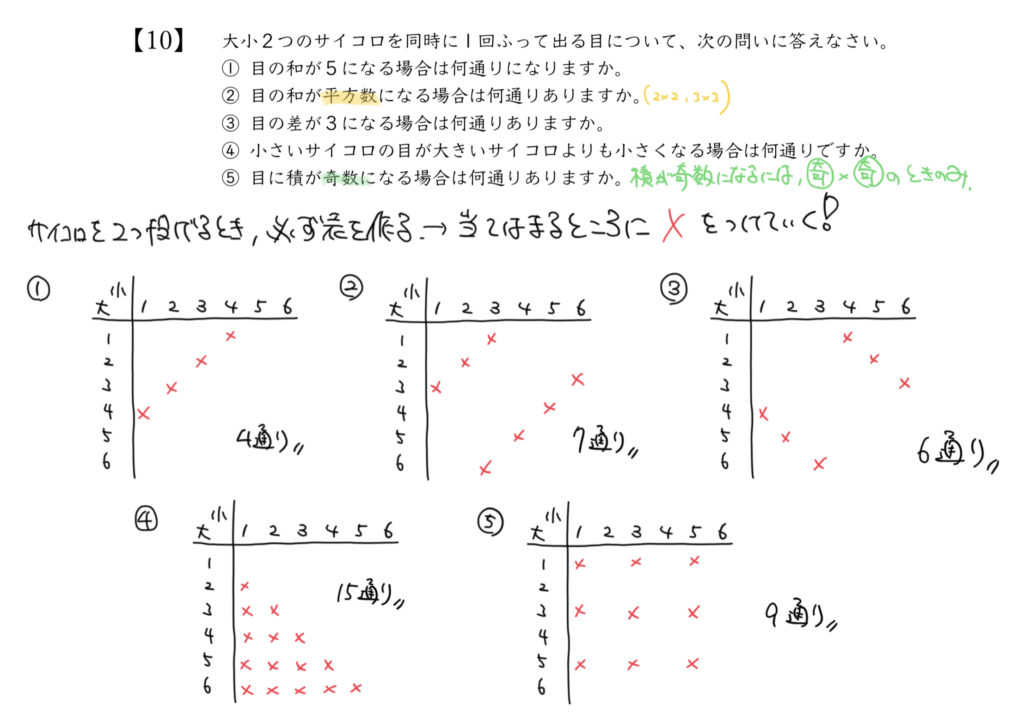
①4通り
②7通り
③6通り
④15通り
⑤9通り
この記事を書いている人はこんな人


解説を読んで「 場合の数 」を攻略しよう!
STEP1:目の和が5になる場合を調べよう
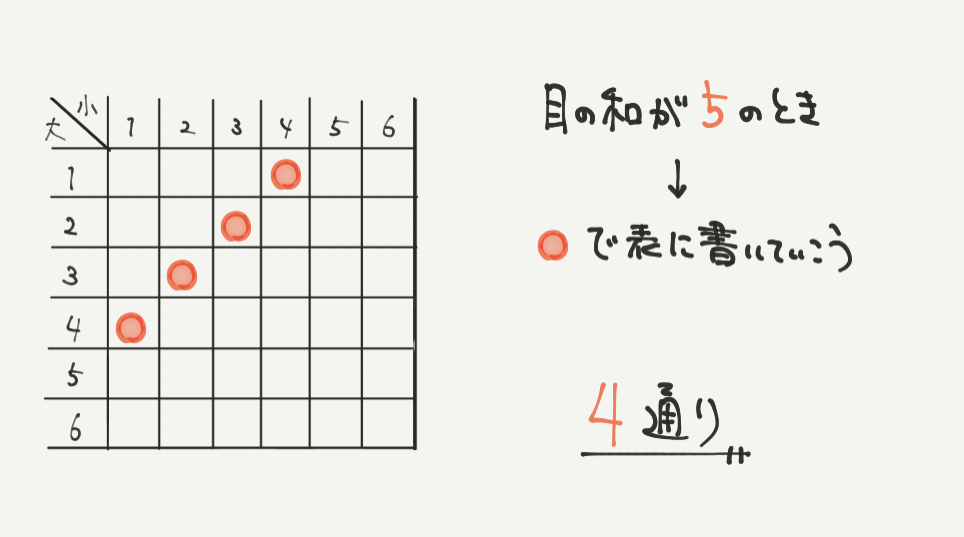
サイコロが2個出てくる問題は必ずこの表を書いて求めましょう。
色々やり方あると思いますが、これが一番確実でミスが少ないやり方だと思います。
また表を書くとき、どちらが大きいサイコロか、小さいサイコロか書いておきましょう。
今はまだ初歩の問題ですが、だんだんむずかしくなってくるので、
今のうちから書いておくクセをつけておきましょう。
①目の和が5になる組み合わせは(1、4)(2、3)といった組み合わせになります。
 わかみや先生
わかみや先生ここは楽勝だと思います。
STEP2:目の和が平方数になる場合を調べよう
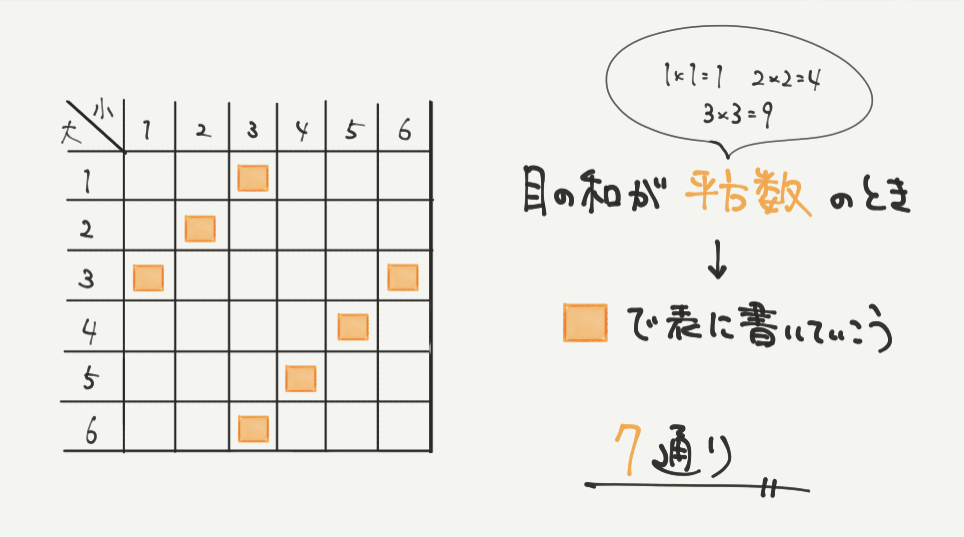

②平方数をわすれてしまうと解けない問題でした。
平方数は□×□のように、同じ数がかけられている数のことです。
今回だと、1×1=1、2×2=4と3×3=9の3つがありました。
1は足し算で作れないので、足して4、9になる組み合わせをさがしましょう!
すると(1、3)(3、6)などが当てはまります!
よって7通りが答えとなります。
STEP3:目の差が3になる場合を調べよう
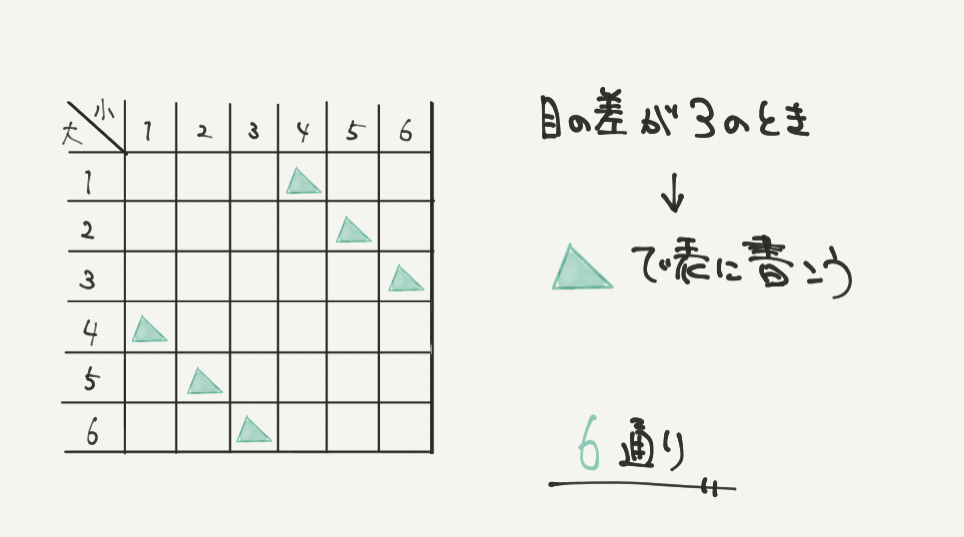

目の差が3になる場合を数えていきましょう。
差が3になるサイコロの組み合わせは(1、4)(2、5)(3、6)などになります。
このように数えていくと全部で6通りとなります。
STEP4:小さいサイコロの目が大きいサイコロよりも小さくなる場合を調べよう
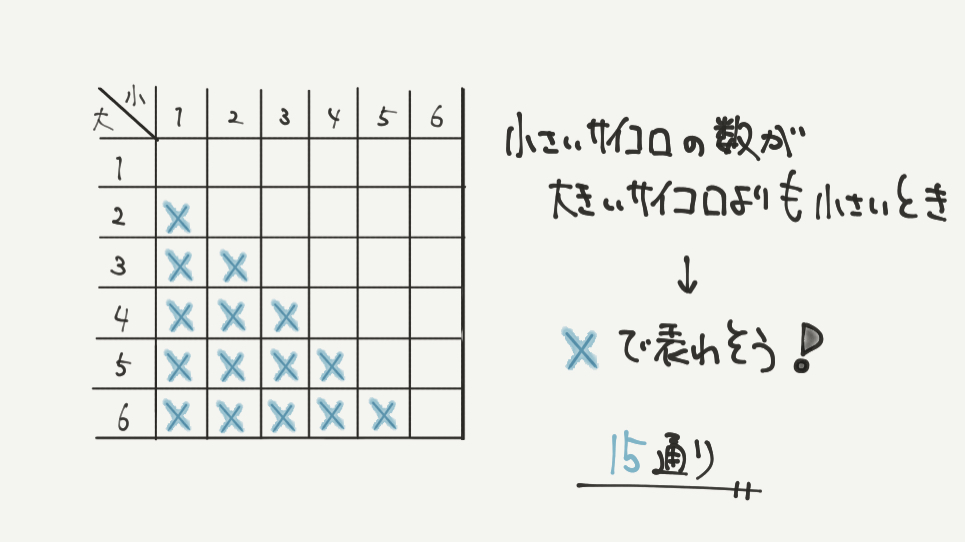

④しっかりと数えましょう。
小さいサイコロが大きいサイコロよりも小さい数になる場合は図の通りです。
たとえば(小、大)=(1、2)(3、4)(2、6)などの数が当てはまりますね。
すると✖︎にように数えることができますので、15通りと書き出しましょう。
STEP5:目に積が奇数になる場合を調べよう
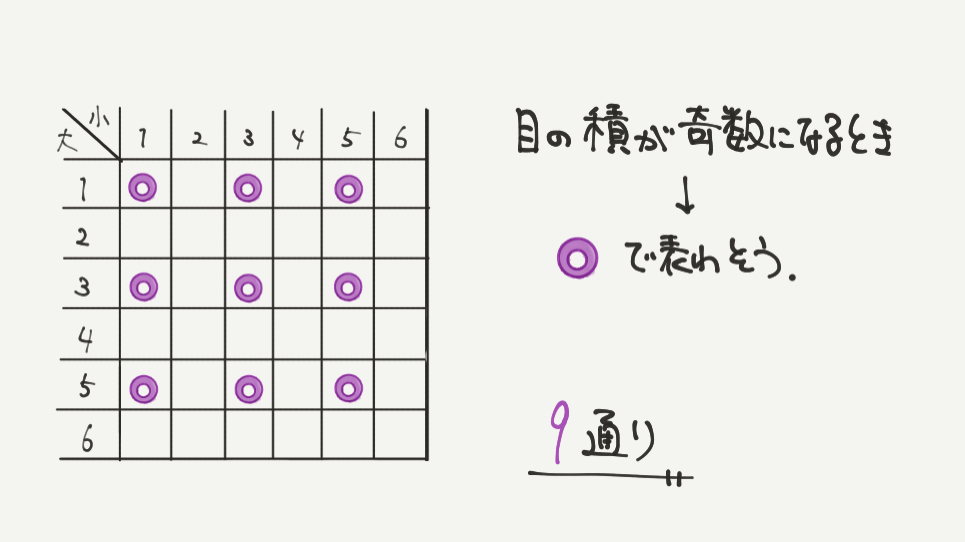

⑤かけ算の結果が奇数になるとき、考えられるのは
奇数×奇数のときのみです。
よって当てはまる数は奇数同士の(1、1)(1、3)(3、5)などの組み合わせになります。
数え上げると9通りとなりますね!!

2つのサイコロを使って出る目を求める問題のまとめ
「 場合の数 」の問題で大事なポイント
サイコロを2つ回すときの考え方
・表を書いてリストを書こう
・全部で36通りある
・当てはまる項目に印をつけよう
以上で今日の問題は終わりです!
最後まで読んでくれてありがとうございました!!
次の問題で会いましょう!!!