【中学受験攻略】白い石と黒い石を並べる場合の数に挑戦！並べ方は全部で何通り？

はじめに

今日は「 場合の数 」の問題の6問目です！
これまで「場合の数」の問題を5問解いてきましたね！
前の問題を解きたい受験生は下の記事をクリックしてみてください！

どっちのパターンで解いても正解なので、みなさんが解きやすいやり方で問題を解くようにしましょう。
「樹形図」と「□の図」を使った場合の数は下の問題から復習できますので、
時間があれば絶対にチャレンジしてみて下さいね！

「 場合の数 」の問題に挑戦ちょうせん！

白石2こ、黒石3この合計5このご石を横1列に並べます。並べ方は全部で何通りありますか。

解答

この記事を書いている人はこんな人

解説を読んで「 場合の数 」を攻略こうりゃくしよう！

STEP1：問題文を図になおそう

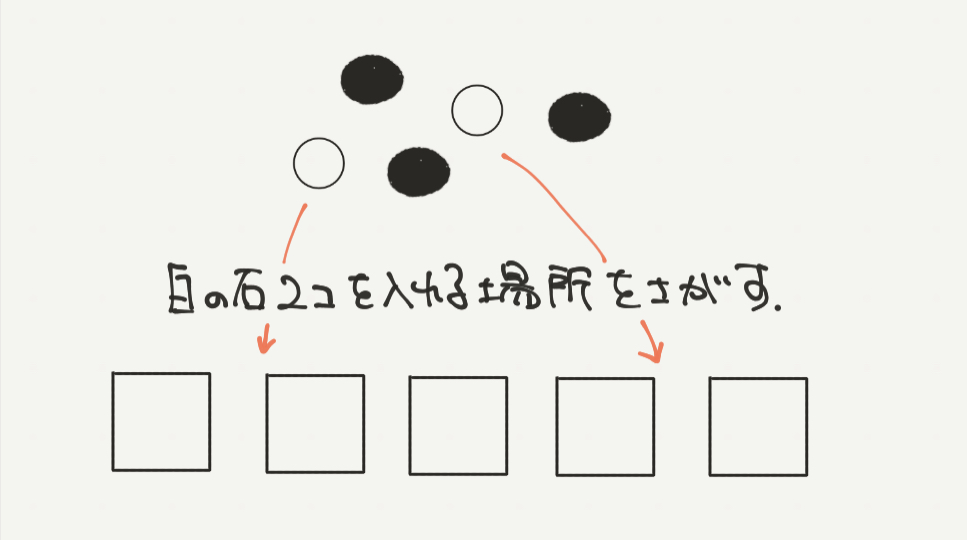
今回は白石と黒石が2こ、3こあるのでそれらを並べていきます。
ですが並べ方はとてもかんたん。
白石2こを□□□□□の中に入れる方法を考えればいいだけです。

黒石については考えなくていいんですか？という疑問があるかもしれませんが、
黒石の場所は考える必要はありません。

なぜなら・・・
□○□○□：白石の場所が確定したら
●○●○●：黒石の場所も自動的に決まるからです。

STEP2：□を作って白石が入る場所を考えよう

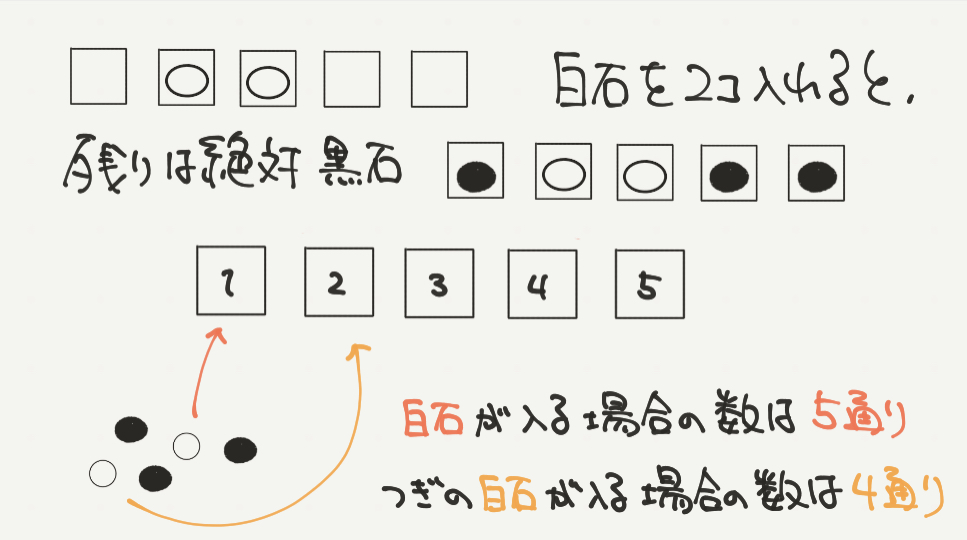
なので、□□□□□の中から２か所選んで白石を入れていきましょう。
すると1こ目の白石が入る場所は1、2、3、4、5の5通りあります。
そして1こ目の白石が入ると2こ目の白石が入る場所は白石の場所以外の4通りとなります。

STEP3：かぶりを考えて答えを出す

なのでふつうに考えると5通り×4通り＝20通りが答えと考えることができます。
しかし、これは正解ではないので注意して下さい！！
なぜなら「かぶり」があるからです。
下の図を見て考えましょう！！

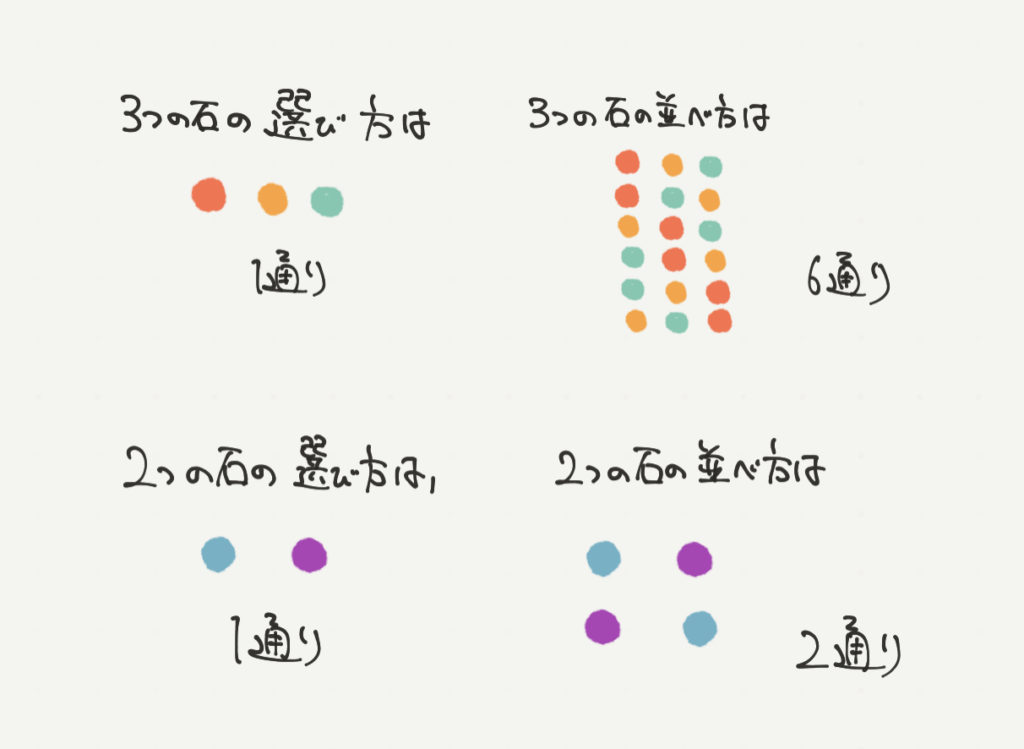
前の問題で石の選び方と並べ方のちがいについて説明しました。

石の選び方と並べ方は全く考え方がちがいます。
石2こから2こ選ぶとき、選び方は当然1通りです。（あたりまえですね）
そして2この石の並べ方は（●●、●●）2通りです。

つまり、STEP2で解いた5通り×4通り＝20通りだと、
（●●、●●）のように同じものを2こ数えてしまっていることになります。

なので、場合の数はこのかぶりをなくすために20通りを2で割ります。（かぶりの数が2倍あるので！）
よって20通り÷2＝10通りとなります。

STEP4：別解で樹形図を書いてみよう

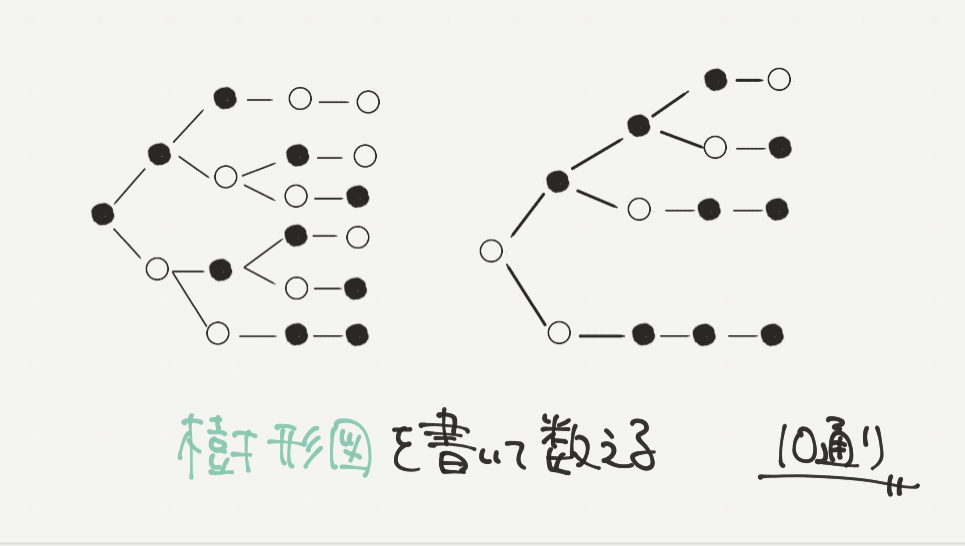
ちなみに樹形図を書くと上の図のように求めることができます。
樹形図はご石の数が少ないときには解けますが、数が多くなってしまうと大変です。
できればSTEP1、STEP2、STEP3の解き方で解いてみて下さいね！

5つのご石を横一列に並べる場合の数を求める問題のまとめ

「 場合の数 」の問題で大事なポイント

「 樹形図 」の考え方
・樹形図は木から枝が生えるように、線をつなげて調べる方法です
・今回は石の数が5こだったのでかんたんにかけましたが、
　数が多くなると解けなくなってしまうので気をつけましょう
「□：ボックス」の考え方
・□□□□□の中に白石が何こ入ることができるのかを考えました
・かぶりに注意して多く数えすぎないようにしましょう

以上で今日の問題は終わりです！
最後まで読んでくれてありがとうございました！！
次の問題で会いましょう！！！

その他の単元の問題の復習はこちらから！