はじめに
みなさんこんばんは!!「さんすうがく」の赤い小人です。
本日は「 図形の移動と構成 」の単元の、よくある図形を回転させる問題です。
受験でも見かける問題たちなので、ぜひ一緒に解いていきましょう!
よろしくお願いします!!
等積変形と図形の移動について確認しよう
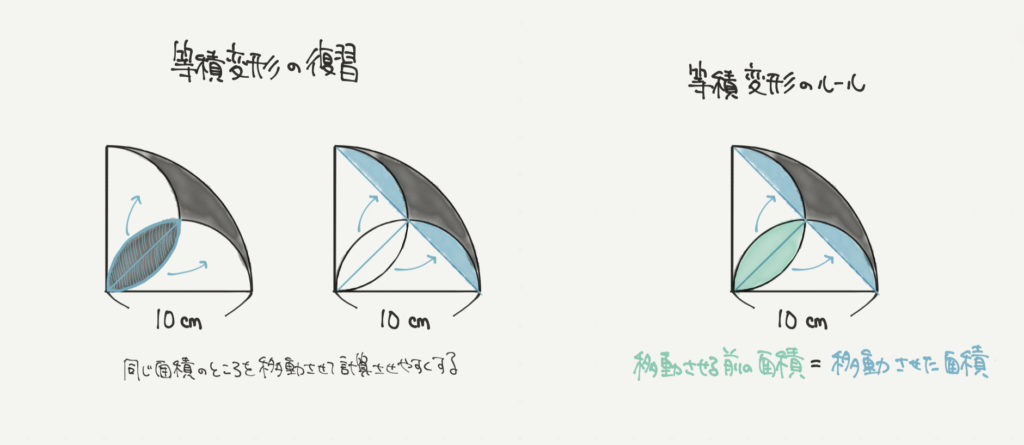
まず今回の問題を解くときに大切になる考えが「 等積変形 」、そして「 図形の移動 」です。
等積変形とは、ある図形の形を変えて別の同じ面積の形に変えることでした。
たとえば、上の図では黒の部分の面積を青いところに移動させていますね。
こうすることで面積をかんたんに求めることができました。
等積変形や図形の移動をするときの大切なポイントは、
「移動させる前の図形の面積=移動させた後の図形の面積」にすることです。
ちがう面積なのに移動させてしまうと、不正解になってしまいます。
必ず同じ面積を移動させたり、変形させたりするようにしましょう!
等積変形の復習はこちらから!

30°、60°、90°三角形の秘密
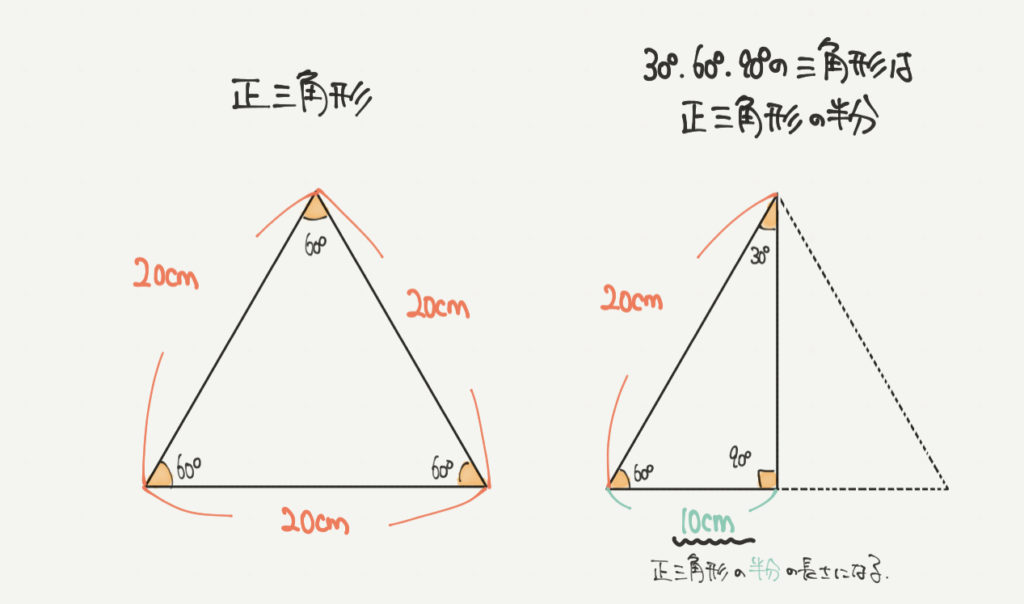
次にポイントになるのが正三角形と30°、60°、90°三角形の秘密についてです。
30°、60°、90°三角形は長い辺の長さが短い辺の長さの2倍になるルールがあります。
この図では一辺20cmの正三角形について説明しています。
30°、60°、90°三角形は正三角形の半分なので、短い辺の長さは20cmの半分の10cmとなります。
図形の問題ではこのような三角形の長さの知識を使う問題も出てきます。
正三角形の図形の知識を使う問題はこちらから!!ぜひ解いてみてください。

「 図形の移動と構成 」の問題に挑戦!
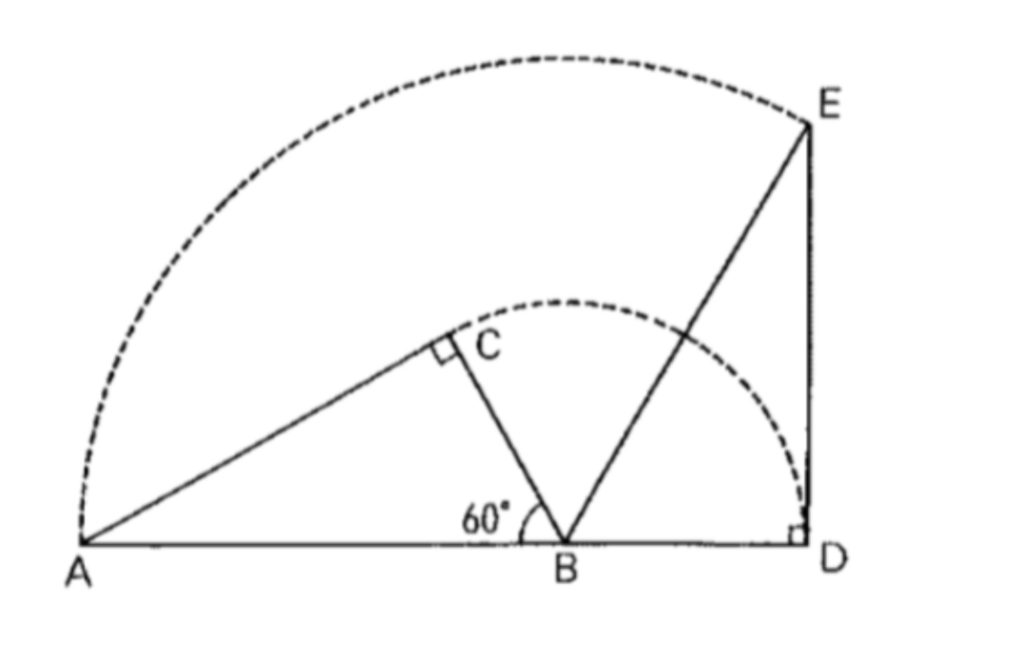
下の図の三角形ABCは直角三角形で、辺ABの長さは6cm、角ABCの大きさは60度です。いま、三角形ABCを、点Bを中心として、三角形EBDに重なるまで回転させたところ、3点A、B、Dが一直線になりました。円周率3.14として、次の問いに答えなさい。
① 点Aが通ったあとの線の長さは何cmですか。
② 辺ACが通ったあとの図形の面積は何㎠ですか。
解答は次のページから!