目次
はじめに
みなさんこんにちは。「さんすうがく」の赤い小人です。
今日も「 図形の移動と構成 」の問題にチャレンジしましょう。
はい!よろしくお願いします。
前回の記事では「 線対称 」について勉強しましたね。
今回は「 点対称 」について説明しています。言葉の意味がわかればそんなにむずかしくないのでぜひ一緒にがんばりましょう!
「 線対称 」の問題を復習したい受験生はこちらから!!

「 点対称 」について理解しよう
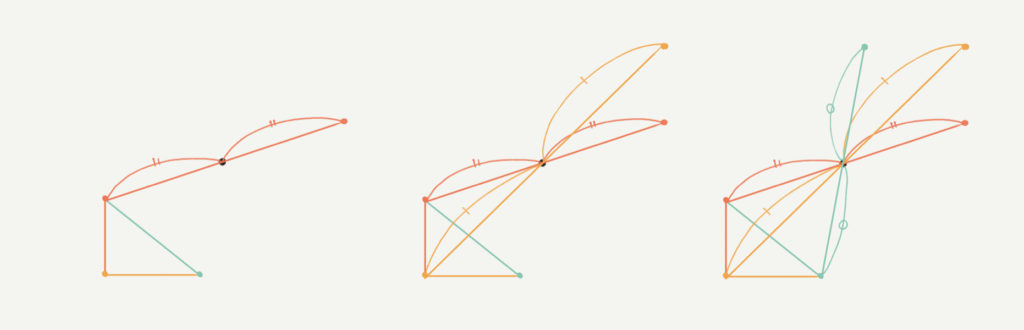
まずは「 点対称 」について説明します。
対称とは、左右で全く同じになると言う意味でした。
ですので、点対称とはある点に対して対称と言う意味になります。
まだよくわからないですよね?
たとえば上の三角形を見てみてください。
それぞれの点(●、●、●)と中心の点●があります。
まずは●と●を見ていきましょう。●から●の長さと同じだけはなれている点が●と点対称の点になります。
同じように●と●の点も考えて線を引いて点を書いてみると、三角形を作ることができると思います。
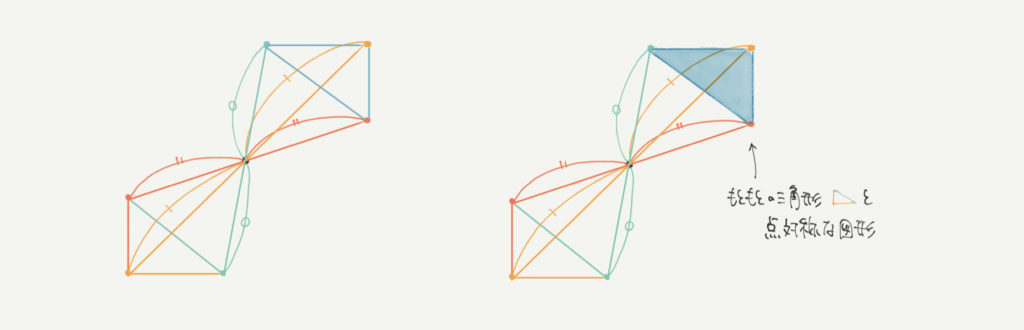
ポイントになるのは点対称の基準になる点●です。
この点●がないと点対称の図形は作れませんので、必ずどこの点●が基準になっているのか考えるようにしましょう!
「 点対称 」の問題に挑戦!
下の図は、点Oを中心とした点対称な図形です。これについて次の問いに答えなさい。
① 点C、点Gに対応する点はどれですか。
② 辺KLに対応する辺はどれですか。
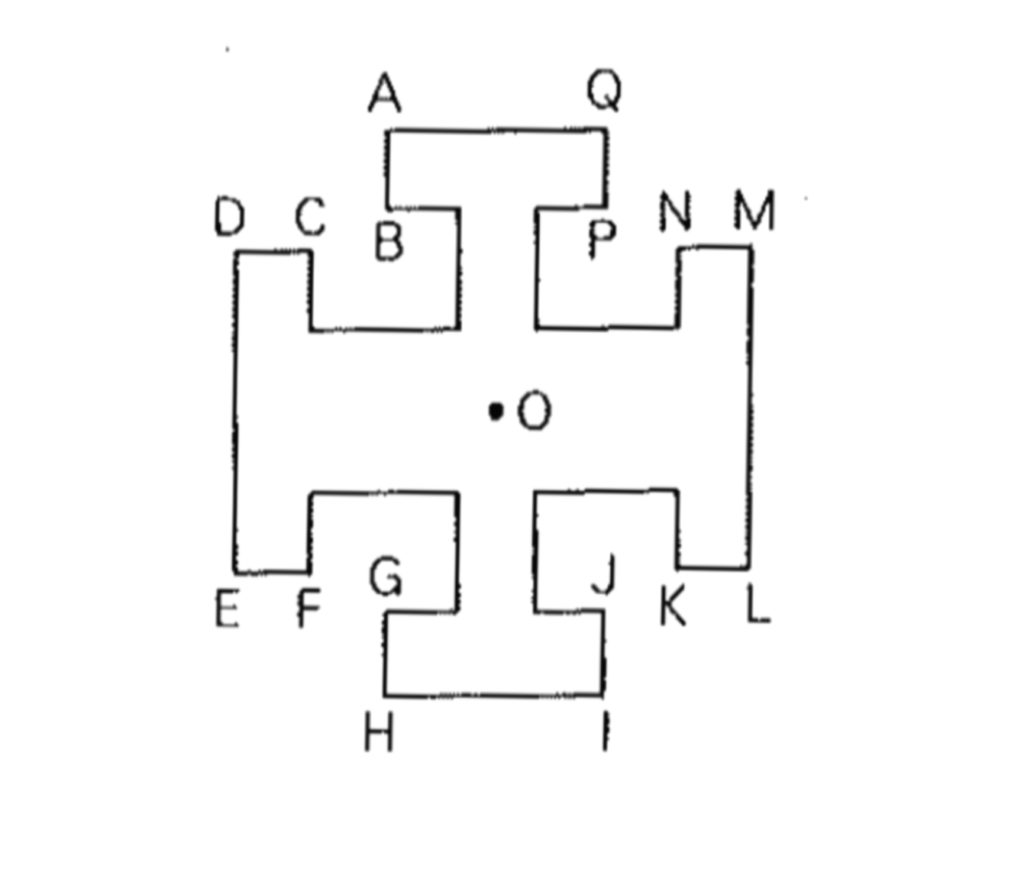
解答は次のページから!