目次
はじめに
みなさんこんにちは。「さんすうがく」の赤い小人です。
本日は「 図形の性質 」の問題について勉強していきましょう。
ていねいに解説していきますので、ぜひ最後までついてきてくださいね!!
はい!今日もよろしくお願いします!
今日はどんな問題なんですか?
今日解く問題は「 図形の性質 」を理解して「 線対称 」と「 点対称 」に分類するといった内容です。
今までの記事のふりかえりでもあるので、自信のない受験生は下の問題たちから解いてみてください。
「 線対称 」と「 点対称 」の復習
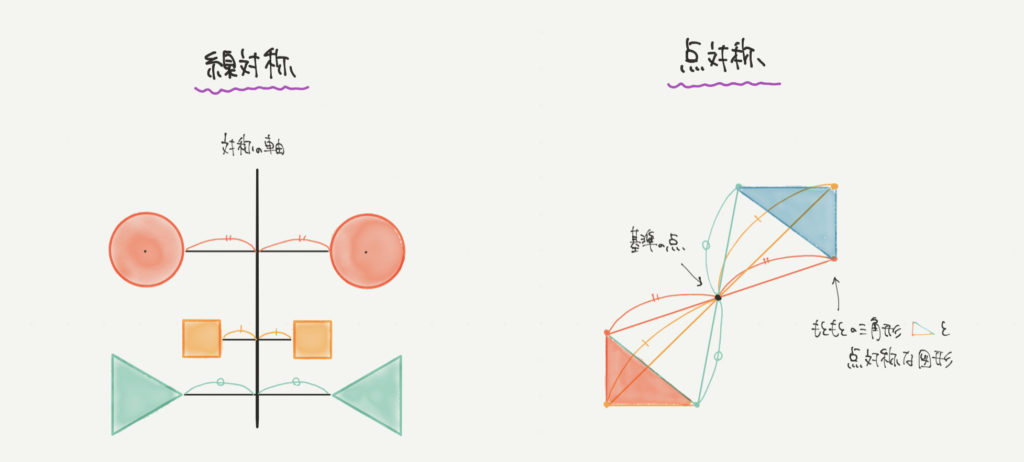
線対称とは、ある線に対して対称(左右同じ)になると言う意味でした。
ですので、ある図形から線までの長さと同じだけはなれたところに線対称の図形ができます。
点対称とは、ある点に対して対称(左右同じ)になると言う意味でしたね。
右図のように赤い三角形があるとすると、基準となる点●に対して同じ長さだけはなれたとことに点対称な図形を作ることができます。
ポイントは基準となる点●を見つけることです!
ある図形が点対称かどうかを調べたかったら、基準の点を見つけて、点からの長さが同じかどうかを調べてみるようにしましょう!
線対称の復習問題はこちらから!!

点対称の復習問題はこちらから!!
それでは問題にチャレンジしていきましょう!!
「 図形の性質 」の問題に挑戦!
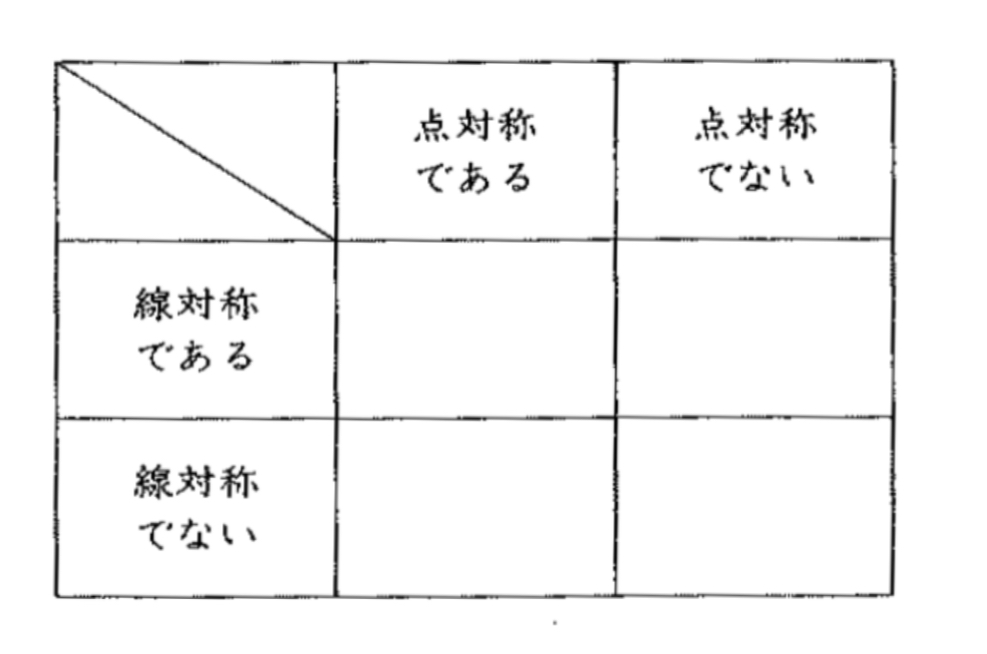
次のア〜コの図形を、下の表のように、分類します。空らんに、当てはまる記号を書き入れなさい。
- ア:正三角形
- イ:直角二等辺三角形
- ウ:二等辺三角形
- エ:直角三角形
- オ:正方形
- カ:長方形
- キ:ひし形
- ク:平行四辺形
- ケ:正五角形
- コ:正六角形
解答は次のページから!