はじめに
 わかみや先生
わかみや先生みなさん、こんにちは!「さんすうがく」のわかみや先生です。
大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います!
前回までの円順列や場合分けに引き続き、今回もSPIの難関の単元にチャレンジしていきましょう。
確率は算数や数学嫌いの原因なった人も多いんじゃないでしょうか?
私も大学時代は中学受験、高校受験の塾講師を務めていましたが「確率」だけは大の苦手でした。
「確率」を解き進めていく中でのコツは、求めている数字の意味を正しく理解することです。
今計算しているのが 何の数なのか、求めている数に抜け漏れはないのか、
数字に着目して問題を解いていきましょう。
この記事を書いている人はこんな人


「さんすうがく」のSPI対策では「SPI&テストセンター超実践問題集/ナツメ社」の問題を参考に使用させていただいております。このテキストをベースに解説していますので、ぜひお手元に用意していただけるとより理解が捗るかと思います。
[92]問題に挑戦!
答えを見るにはここをクリック!
①1/64
②7/32
[92]解説を見てみよう!


確率の問題はタイトルにもあるように、数字の一つ一つが持つ意味を理解しながら解いていきましょう。
①ヒナが成鳥になる確率は1/8,なので、2羽とも成鳥になる確率は
1/8×1/8=1/64になります。
このような問題は確率の基礎になるのでよく確認しておきましょう。
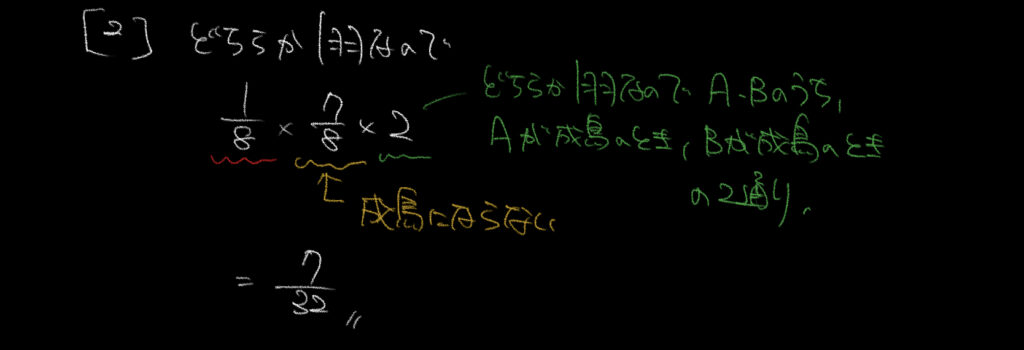
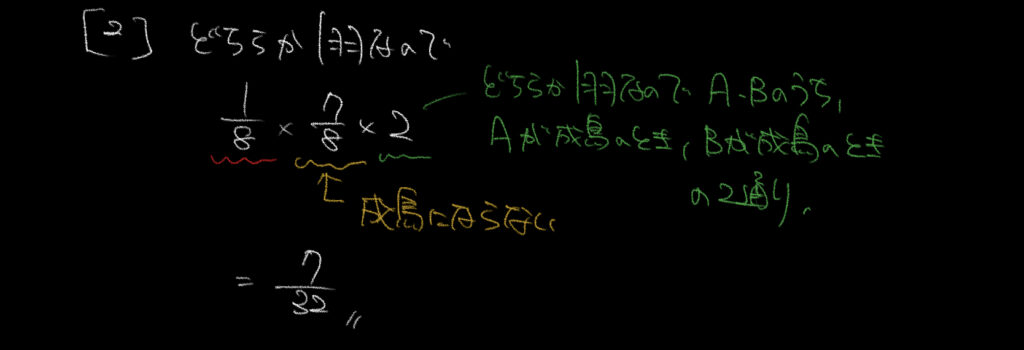
②はどちらか一方が成鳥になればいいので、
1/8×7/8=7/64となります。
ただし、これは初めの1羽が成鳥になった場合です。
解説の緑の部分にも書いてあるように1目が成鳥になる場合と
2羽目が成鳥になる場合の2通りが考えられるので、
7/64×2=7/32と求めます。
[93]問題に挑戦!
答えを見るにはここをクリック!
①5/12
②1/6
③1/12
[93]解説を見てみよう!
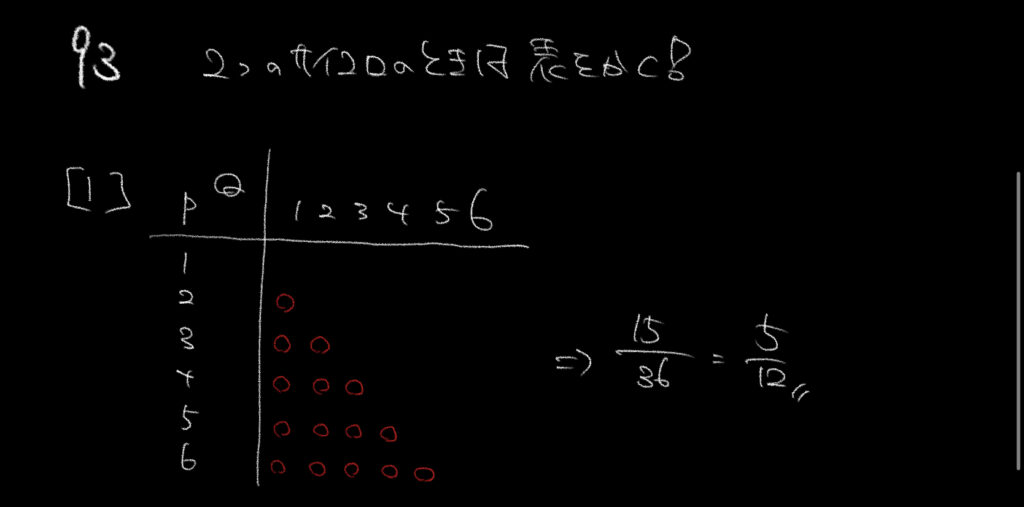
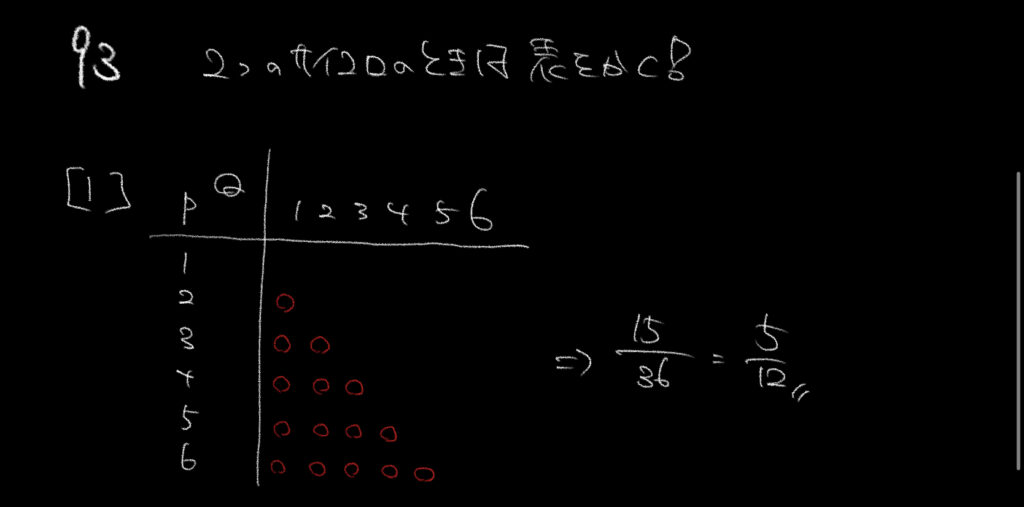
サイコロを投げる問題は必ずこの表を書きましょう。
中学受験生にも教えていることですが、この図を書くことでサイコロの問題の正答率が大幅に変わってきます。
2人がサイコロを投げて出る目の場合は36通り。この中から該当するものに印をつけていきましょう。
①PがQに勝つときなので、PがQよりも大きくなる場合を印で記入していきます。
すると全部で15とわかるので、15/36=5/12となります。


②Pが3以上を出しているので気をつけましょう。
このとき、Qに負けるにはQは4以上を出さなければいけません。
よって印をつけていくと、6/36=1/6となります。
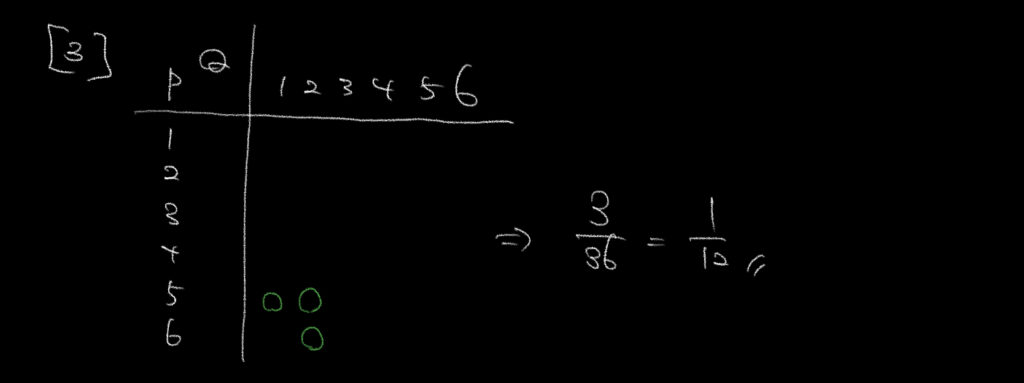
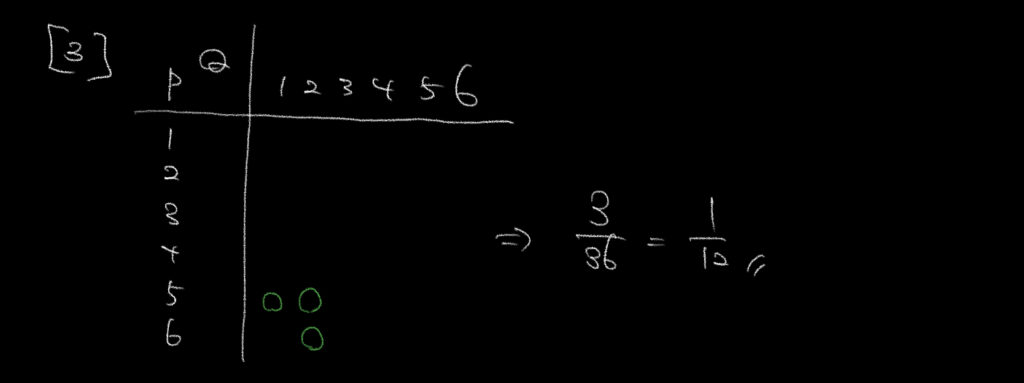
③最後はPが4以上の差をつけてQに勝つ確率を求めよという問題でした。
これは最低でもPが5でないと成立しない条件です。
印を数えると全部で3通りしかないので3/36=1/12となります。
このようにサイコロが2つ出てくる問題は必ず表を書くようにしましょう!


[94]問題に挑戦!
答えを見るにはここをクリック!
①4/9
②19/27
[94]解説を見てみよう!
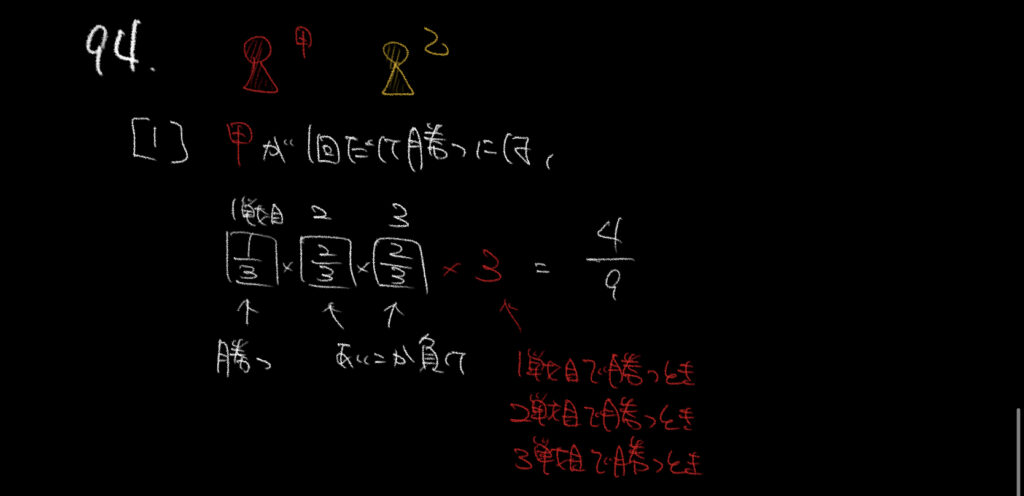
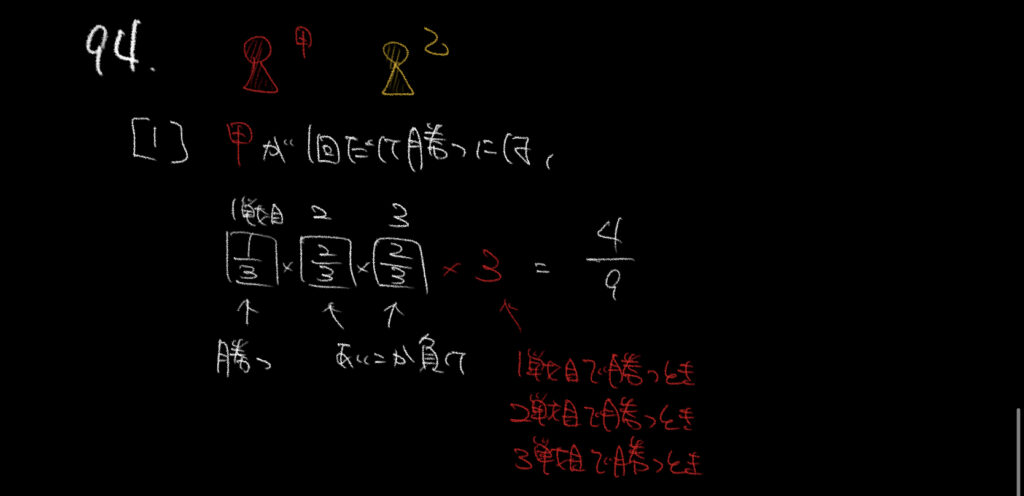
①甲が1回戦で勝つ確率を求めます。
1回戦で勝つには1/3の確率が必要です。
また、今回は1回だけ勝つ確率なので残りの2回は負ける必要があります。
2/3というのは負ける確率のことです。
これを計算して、
1/3×2/3×2/3=4/27
計算を求めると4/27となります。
ただし、これは甲が1回戦で勝つ場合の確率でした。
Pは他にも2回戦で勝つ確率、3回戦で勝つ確率の3パターンがあるので
4/27×3=4/9となります。


②少なくとも1回は〜というような問題は「余事象」を使って解いていきましょう。
甲が少なくとも1回は勝つ確率=全部の確率–甲が全部負ける確率、で求めることができます!
2/3は甲が1回も勝たない確率のことで負けとアイコのときです。
よって甲が全部負ける確率は、2/3×2/3×2/3=8/27 です。
全部の確率は1なので、1–8/27=19/27と計算することができました。
「余事象」の問題はこちらから挑戦してみてください。


[95]問題に挑戦!
答えを見るにはここをクリック!
①1/15
②8/15
[95]解説を見てみよう!
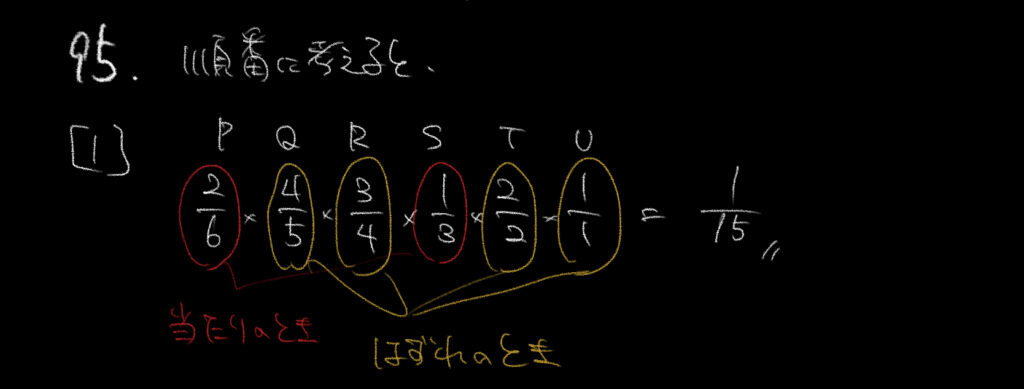

一つずつ数字を追って考えましょう。
①P,Q,R,S,T,Uの6人の順番でくじを引きます。
Pがまず当てるので6本のくじのうち当たりくじの2本を引く確率は2/6=1/3です。
Q,Rは共にハズレを引くので5本あるくじのうちのハズレ4本、4本あるくじのうちのハズレ3本を引きます。
Sは残った3本のうち、あたりの1本を引くので1/3。
T,Uの2人は全部ハズレですが、残っているくじ全部ハズレなので確率は、
2/6×4/5×3/4×1/3×2/2×1/1=1/15となります。
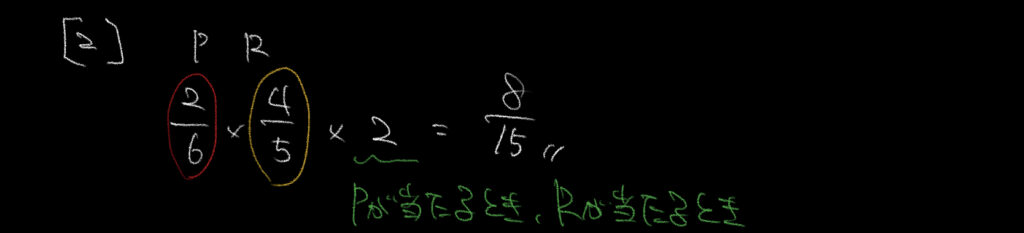
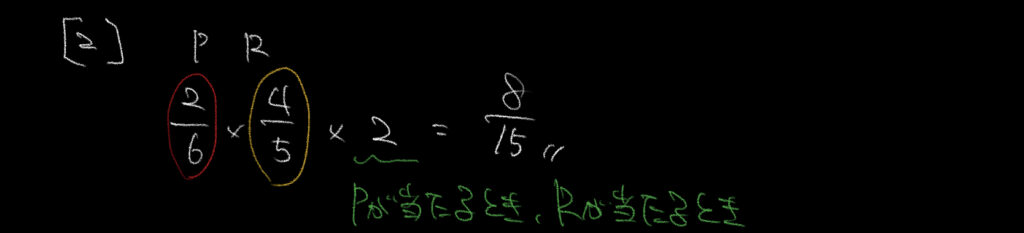
②PとRについて調べていきましょう。
まずはPが当たってRが外れる場合です。
Pが当たる確率は先ほどもやったように2/6=1/3となります。
またRが外す確率は5本あるうちのハズレ4本なので4/5。
よってPが当たってRが外れる場合の確率は1/3×4/5=4/15です。
Pが当たる確率は4/15なので、
逆にRが当たる場合も考えないといけません!
PとQの2パターンがありますので、4/15を2倍して8/15が問題の答えとなります。
[96]問題に挑戦!
答えを見るにはここをクリック!
①1/12
②5/36
[96]解説を見てみよう!
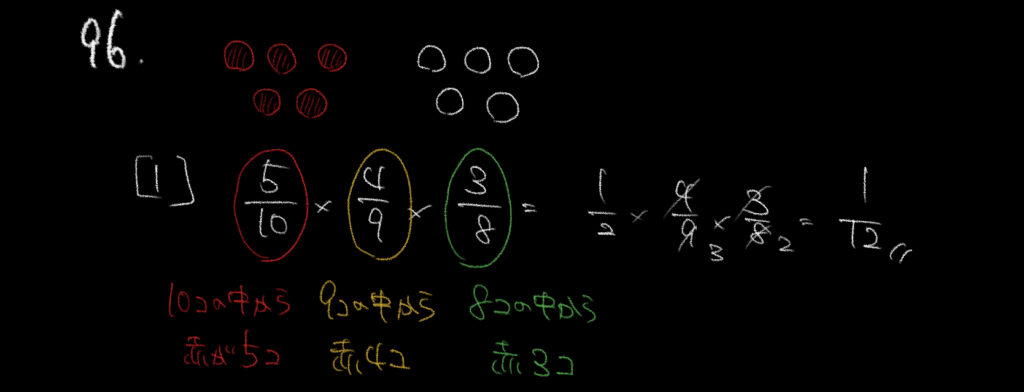

問題文をしっかり読んで、条件を理解しましょう。
①連続で赤が出るので数字を考えていきましょう。
まずは10個の中から5個の赤玉を選ぶ確率です。これは5/10となります。
次に9個の中から4個の赤玉を選ぶ確率です。これが4/9となります。
同様に3個目も8個の中から3個の赤玉を選ぶ確率は3/8です。
よって確率は5/10×4/9×3/8=1/12になります。


②ただし赤玉であれば箱に戻し、白玉であれば戻さないものとするがポイントです。
初めは①と同様にやります。赤は箱に戻すので次も同じ確率になります。
白は箱に戻さないので数は1個減らして9個で計算します。
すると1回目は赤が出るので5/10、赤の玉はそのまま戻すので
2回目に白い玉が出る確率も5/10、白い玉のときは1個減らして、
3回目に赤が出るのは4/9となります。
よって5/10×5/10×4/9=5/36になります。
[97]問題に挑戦!
答えを見るにはここをクリック!
①1/20
②11/20
③9/20
[97]解説を見てみよう!


①ハート♡は16枚中4枚あるのではじめに♡を引ける確率は4/16です。
2回連続♡を出す確率を求めたいので、2回目は15枚中3枚のハートを引く確率を考えましょう。
2回目は15枚中3枚の♡を出せればいいので確率は3/15です。
4/16×3/15=1/20
よって確率は1/20となります。


②①と反対の考えを使いましょう。
16枚中12枚がダイヤ♢以外なので、ダイヤ♢以外を引ける確率は12/16となります。
次に15枚中11枚のダイヤ♢以外を引きたいので11/15になります。
ここから、求めたい確率を計算すると、
12/16×11/15=11/20となります!
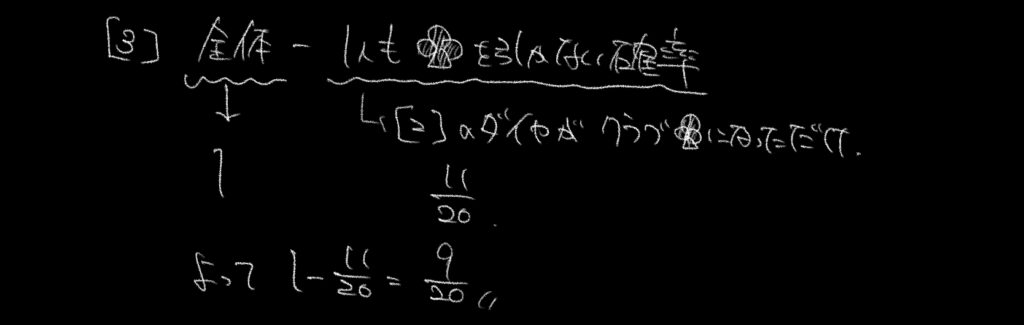
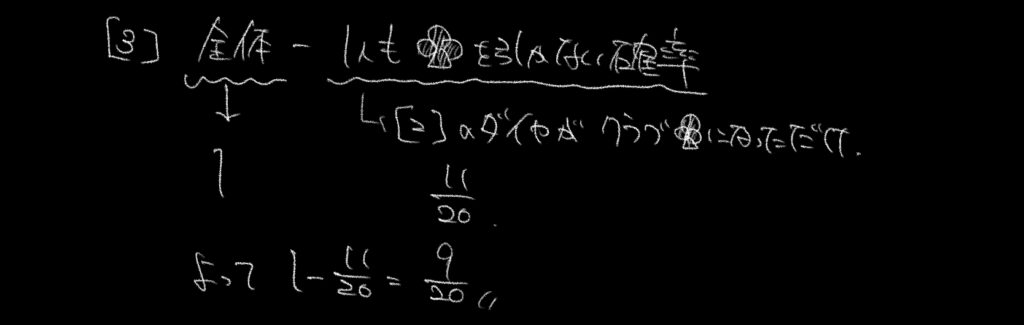
③「2人のうち、少なくとも1人がクラブ♧を引く確率」の時は「余事象」で考えましょう!
全体の確率から1回もクラブ♧を引かない確率を引きます。
これは②で求めたダイヤ♢がクラブ♧になっただけなので、
1回もクラブ♧を引かない確率は11/20になりました!
よって全体の確率から1回もクラブ♧を引かない確率を引くと、
1-11/20=9/20となります!


まとめ
以上がSPIの確率の問題、基礎編でした。
確率は自分の書いている数字が何を意味しているのかをしっかり理解しましょう。
問題によっては条件が特殊な場合があるので、数字の意味を確認しましょうね。
どこの数字が何を表しているのかを把握できれば、確率は問題ないはずです!!
残す後半戦も頑張っていきましょう!かなり難しくなるので要復習です!







