はじめに
 わかみや先生
わかみや先生みなさん、こんにちは!「さんすうがく」のわかみや先生です。
大学生の皆さんへ就職試験対策として本日もSPIに関する情報やコツをお届けしていきたいと思います!
今回もSPIで頻出の「割合と比」の問題になります。後半戦です!!
後半の問題は文章の長い、いわゆる長文問題にチャレンジです。
文章が長いとそもそも時間制限のあるSPIでは焦ってしまいがちですが、
問題文が長いということはその分ヒントも多いということ!
百聞率と歩合の考え方をこの記事で勉強していきましょう!
この記事を書いている人はこんな人


「さんすうがく」のSPI対策では「SPI&テストセンター超実践問題集/ナツメ社」の問題を参考に使用させていただいております。このテキストをベースに解説していますので、ぜひお手元に用意していただけるとより理解が捗るかと思います。
[114]問題に挑戦!
答えを見るにはここをクリック!
①68%
②3.4%減少した
[114]解説を見てみよう!


割合と比の問題も折り返しです!
ここからは少々問題が複雑になってきますので、より慎重に解いていきましょう。
また今回の記事のテーマにもあるように百分率と歩合についておさらいしましょう。
百分率と歩合


割合は上のように百分率(全体を100%と考えるやり方)と歩合(全体を10割と考えるやり方)があります。
それぞれの割合をきちんと理解して、問題を解いていきましょう。
①まずは状況の整理から!
解説にも書いてありますが、与えられて情報を一回整理するところから始めていきましょう。
貸出冊数が696冊で、一人当たりの平均貸出数が1.5冊なので、
借りた人数は696冊÷1.5冊/人=464人と求まります。
よって借りなかった方の生徒は1450人−464人=986人。
この986人は生徒数全体1450人の68%と求めることができます。


②借りられた本が25%増えたので、696×1.25=870冊になります。
今度は借りた人数がわかっているので面積図に書き込んで解いていきましょう。
870冊÷600人=1.45冊/人となり、
1.45冊/人÷1.5冊/人=96.6%
前回の1.5冊/人よりも3.4%減ったことがわかります。


[115]問題に挑戦!
答えを見るにはここをクリック!
①37%
②840cc
[115]解説を見てみよう!
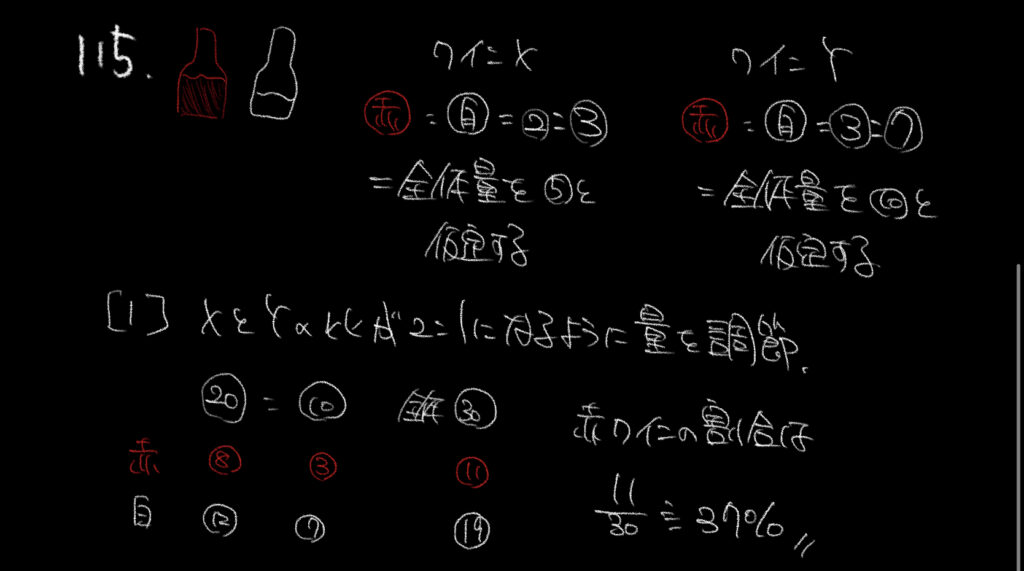
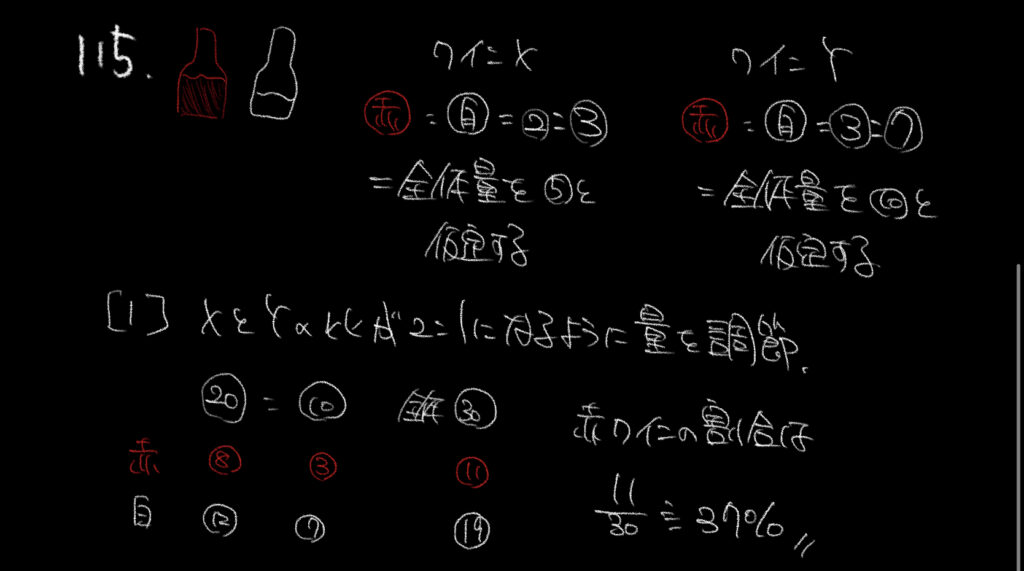
このような比率が複数出てくるような問題はかなりめんどくさくなります。
数字を仮定していって解きやすい形にしましょう。
①ワインXは比率が2:3なので全体量を⑤と仮定します。
またワインYの比率は3:7なので全体量を⑩と仮定することができます。
XとYのワインの量の比率を2:1にしなければいけないのでXの全体量を4倍して、○の20にします。
するとXの中にある赤ワインと白ワインの量もそれぞれ4倍されるので、⑧と○の12となります。
これを足し合わせるとワイン全体の量が⚪︎の30となりますので、
求めた赤ワインの割合から、赤ワインの割合を11/30=37%と求めることができます。


②は全く別の系統の問題でした。先ほどの割合や比率は無視で構いません。
ワインZの全体量を◻︎の42と仮定しましょう!
今回は7等分、6等分しているので最小公倍数の42を全体量として仮定します。
すると、7等分したときに飲める量は□の6、
6等分したときの量が□の7となり差の□の1が20ccとなります。
□の1が20ccなので、求めたい全体量は□の42。
よって20cc×42=840ccとなります。


[116]問題に挑戦!
答えを見るにはここをクリック!
①110個
②120個
[116]解説を見てみよう!
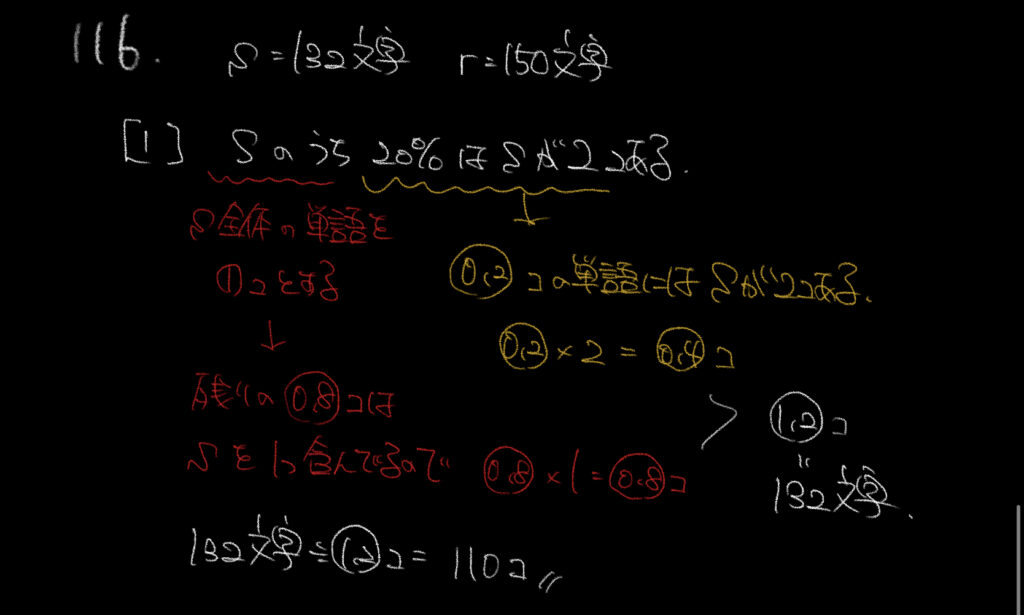
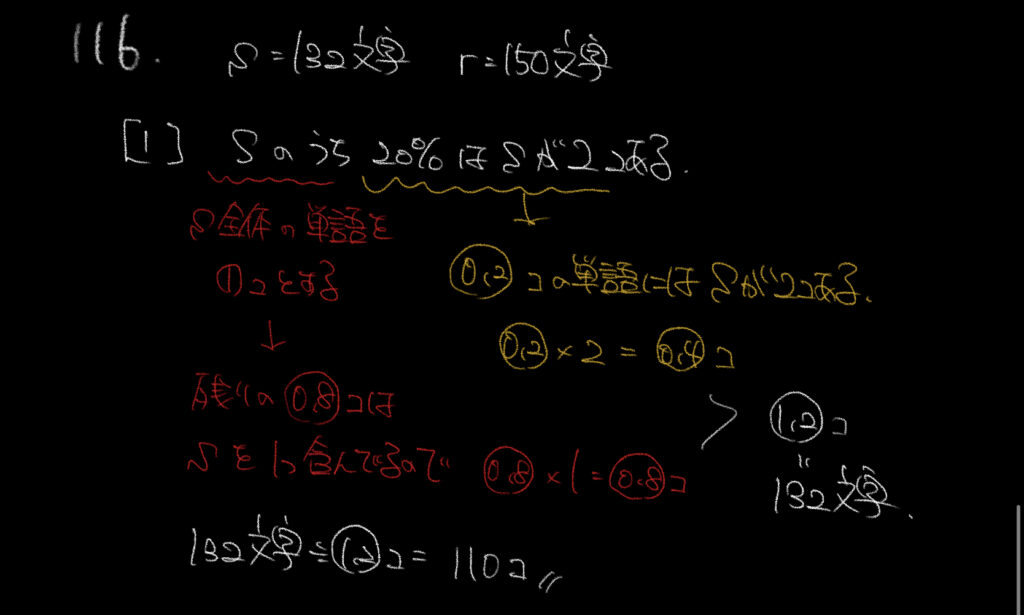
単語数と文字数を混ぜて考えないようにしましょう。
①sの単語数を①と仮定します。
すると20%(○の0.2)はsが2個あるので○の0.2×2個=個数を○の0.4個と表すことができます。
同様に残りの単語数○の0.8はsが1つずつあるので文字数は○の0.8×1=○0.8個となり、
合計文字数を○の1.2と表すことができます。
○の1.2が132文字となっているので、①は110。よって110個となります。
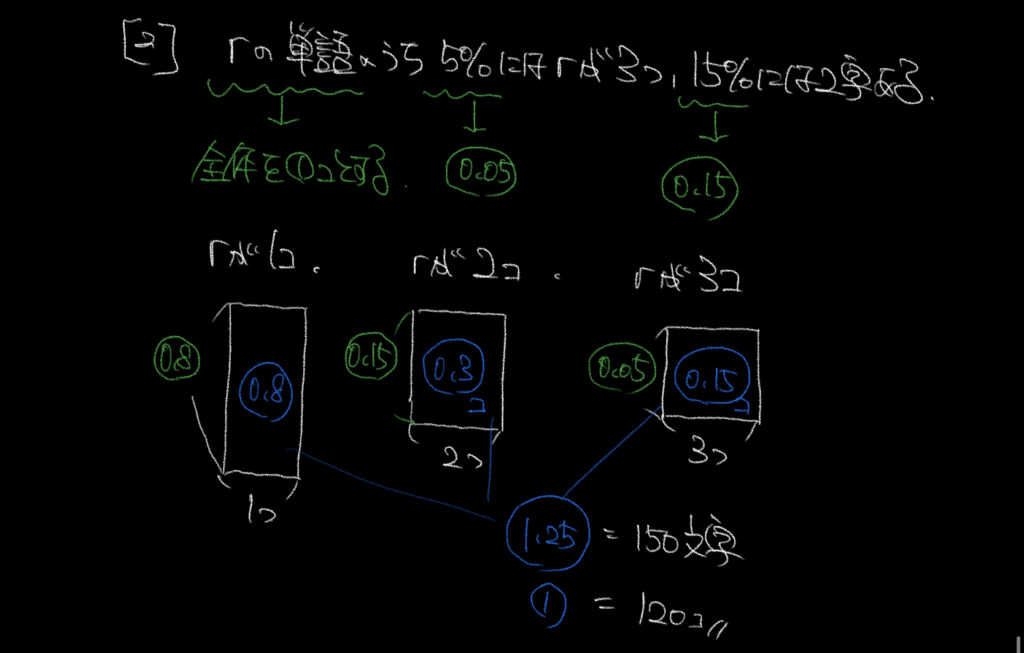

②先ほどと同様に単語数を①と仮定して文字数を○で表していきましょう!
それぞれ面積図を書いていくと、
rが3つの文字数を○の0.15、
rが2つの文字数を○の0.3個、
rが1つの文字数を○の0.8個、と求めることができます。
ここから、文字数全体が○の1.25となり
150文字÷○の1.25=①が120個になります。


[117]問題に挑戦!
答えを見るにはここをクリック!
①43%
②15人
③79.5%
[117]解説を見てみよう!


表の読み取りとの複合問題でした。
まずは分かるところをかたっぱしから表に入れまくります。
解いている順番は赤→黄→緑→青です。
①表からサッカーをした人は前期後期合わせて48人と50人でした。
ここで98人と解答してはいけません!!気をつけてください。
この98人のうち、12人は前期も後期もサッカーを取っているので重複して数えてしまいます。
よって98人から12人を引いた86人がサッカーをとった生徒数になります。
よって86/200=43%となります。
②卓球を選択したうちの30%が野球をとったので、
選択した人を①とすると、野球をとった人は○の0.3となります。
前期に卓球をした人は①で、
足し算で8+15+12+○の0.3=①となります。
○の0.7=8+15+12
○の0.7=35
ここから①が50人とわかり、求めたい30%の人数が15人となります。
③①と同じように考えると卓球経験者は90人。
また、テニスは101人となりますが、そのうちの卓球経験者はすでに数え終えているので(卓球・テニス)(テニス・卓球)の「32人を引いた69人」を足した159人がどちらかの経験者であるとわかります。
よって159/200=79.5%となります。


まとめ
以上で割合と比は終了です!お疲れ様でした。
簡単な問題から、最後はグラフの応用問題まで、幅広く扱ってきました。
SPIの問題は前の記事でも触れた通り、中学受験と同じ考えを使うところが多くあります。
中学受験の算数を扱う「さんすうがく」にも同じ単元があるのでよろしければそちらも参照してください。









