はじめに
 わかみや先生
わかみや先生みなさん、こんにちは!「さんすうがく」のわかみや先生です。
大学生の皆さんへ就職試験対策として本日からSPIに関する情報やコツをお届けしていきたいと思います!
中学受験、高校受験で嫌というほど勉強した算数と数学。
まさか大学生になっても勉強するなんて思いませんよね・・・(私もそう思っていました!)
ですが事実として就職活動においてSPIを導入している企業は多くあります。
面接を受ける前に就活生に最低限の知識レベルや教養があるのかを企業が見定めるものです。
せっかくESや面接内容を準備しても、SPIで躓いてしまっては勿体無い!
でも解説を読んでもイマイチ内容が理解できない!
そんなみなさんに向けてこの記事を作成しました。
このサイトでは中学受験生を対象に作成した「中学受験対策に関する記事」と
就活生に向けた「SPI試験対策の記事」を更新していきます。
ぜひ希望する企業の内定に向け、SPIを一緒に攻略していきましょう!!
この記事を書いている人はこんな人


「さんすうがく」のSPI対策では「SPI&テストセンター超実践問題集/ナツメ社」の問題を参考に使用させていただいております。このテキストをベースに解説していますので、ぜひお手元に用意していただけるとより理解が捗るかと思います。
[66]問題に挑戦!
答えを見るにはここをクリック!
432通り
[66]解説を見てみよう!


SPIはじめの問題は並び方についてでした。
これは苦手としている人が多い傾向にあると思います。
めちゃめちゃ気持ちわかります!笑
ですが、そうも言ってられません。なるべくわかりやすく解説していくので頑張ってついてきてください!
まずPとCについて理解しよう!!
参考書でも書いてあると思いますが、解説で使われているPが順列で、Cが組み合わせです。
Pを使う計算の場合はリレーや背の順のように順番が関係あるときの考えです!
一方で選挙や学級委員を選ぶとき、選ばれる順番は関係ないですよね?
このような違いを理解した上で、問題を解いていきましょう。


例えば、こちらの問題は画用紙に色を塗り分ける問題です。
面積の違う部分の色の塗り分けになると色分けの順番がとても大事になります。



大きな部分に赤を塗るか、青を塗るかで
出来上がる絵が全く変わりますよね!

今度はこちらの生徒を選ぶ問題です。
8人の中から3人を選べばいいわけです。ABCの順で選ぼうと、BACの順で選ぼうと、なんでもいいわけです。
こういう順番が関係なく、組み合わせさえ分かればいいときはCを使って計算していきます!
ボックスの考え方
中学入試で小学生を教えるときに使う考えです。
僕はこのやり方に何度も救われました。
順列であれ、組み合わせであれ、ボックスは必ず使う考えです。確認してみましょう。


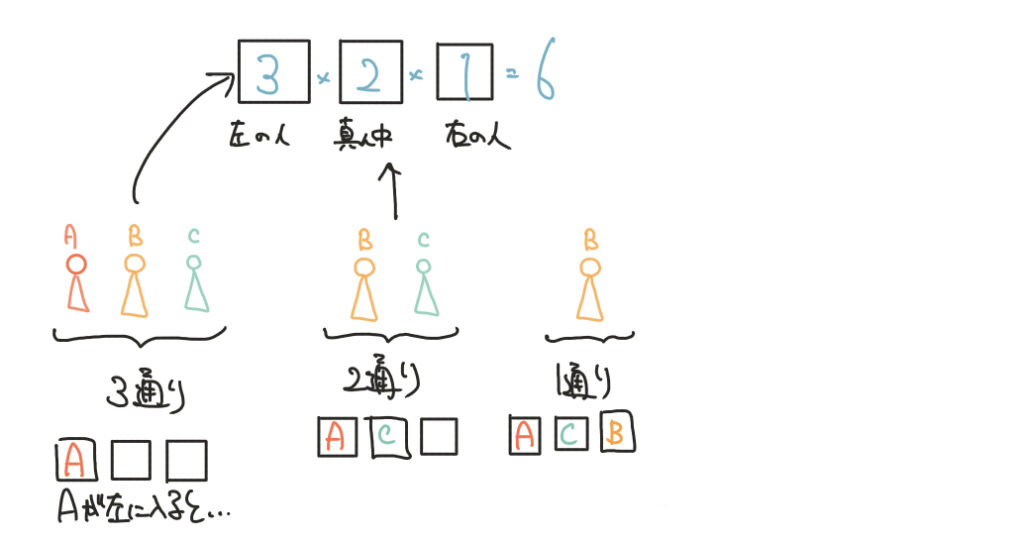

例えばABCの3人が一列に並ぶときを考えてみましょう。
まず初めに左に並ぶ可能性のあるのはA,B,Cの3通り。
ここでAが入ったとしましょう。
次に入る可能性があるのがBかCになります。(Aはもう並んでいるので入る可能性はありません。)
なので、ここは2通りになります。ここでCが入ったとすると、
最後に残った部分にはBが必ず入ります。よって1通り。
この考え方がボックスです。
[67]問題に挑戦!
答えを見るにはここをクリック!
12通り
[67]解説を見てみよう!


今回もボックスの考え方を使って解いていきました。
ここで注目していただきたいのが、水曜日と金曜日です。
料理教室が月曜日なら、テニスの候補は火、水、木、金の4日ありますが、
料理教室が水曜日、金曜日ならテニスの候補が3日になります。
なので、今回は場合分けで解きました。
料理教室が月曜の時、テニスは4日の中から2日選ぶだけなので組み合わせの式を使います。
一方で、水曜日の時は、テニスは3日の中から2日選ぶので3通り。
このように計算することで12通りと答えを求めることができます。


[68]問題に挑戦!
答えを見るにはここをクリック!
9通り
[68]解説を見てみよう!


SPI対策で使われる余事象とは
今回のポイントは余事象についてでした。
余事象について、コインを5回投げる時を例に説明します。
例えばコインを5回投げたときに一回以上表が出る場合の数を数えたい場合、
1回表が出る場合+2回表が出る場合+3回表が出る場合+4回表出る場合+5回表が出る場合、を計算するより、
全部の場合の数–(5回とも裏が出る場合)をした方が効率がいいのはイメージできますでしょうか?
今回の問題では「少なくともオランダかフランスのどちらかを入れる選び方」と言われているので、
全部の場合の数–(オランダとフランスが選ばれない場合)を計算してあげました!
余事象の問題はこちらから勉強できます!

[69]問題に挑戦!
答えを見るにはここをクリック!
34通り
[69]解説を見てみよう!


またまたボックスの考えを使っていきます。
また、余事象の考えも使います。
世界史か日本史のどちらかが入っている場合の数は
全体から日本史4問の場合を引くのと同じになります。
日本史が4問出題される場合は問題全てが出題される1通りしかないので
全体(35通り)から1通りを引いた34通りが答えになります。
[70]問題に挑戦!
答えを見るにはここをクリック!
①120通り
②120通り
[70]解説を見てみよう!


ここでも余事象の考えを使ってみましょう!
女性は4人しかいないので、①の条件に当てはまらないのは男子が一人の時と全員が男子の時のみ。
全体は126通りあって、その中で男子一人選ぶ場合の数は5通り、男子全員が選ばれるのが1通りなので
126-5-1=120通りになります。
②もそこまで難しくありません!
ペアを作りたいので男子から2人、女子から2人選びます。
ここも組み合わせの考えです。間違えないようにしましょう!
そして最後に、男女のペアの組み合わせについて考えましょう。
AC、BDのときと、AD、BCの2通りあるので、最後に2を掛けるのを忘れないようにしましょう。
[71]問題に挑戦!
答えを見るにはここをクリック!
①10通り
②6通り
[71]解説を見てみよう!


①3個の組み合わせは数えて求めた方が早いと思ったので、数えて調べました。
ですが、場合わけはしっかり行いましょう。
まずは3色とも同じとき、次に3色も違うとき、最後に全部で2色のときです。
はじめの2つはすぐに求めることができますが、最後が少し面倒でした。
場合分けで調べ上げるときは、調べた数に抜け漏れがないか、場合分けのパターンに抜け漏れがないかを確認しましょう!
しっかり数え漏れのないようにしましょう!
②も同様ですが、ここも余事象を使って楽に計算しましょう。
先ほどの説明でもやりましたが、7色の色の組み合わせは、
選ばれなかった2色の組み合わせと同じになります。
なので7つではなく、2個の選び方を求めればOKです。賢くいきましょう!
[72]問題に挑戦!
答えを見るにはここをクリック!
①48通り
②18通り
[72]解説を見てみよう!
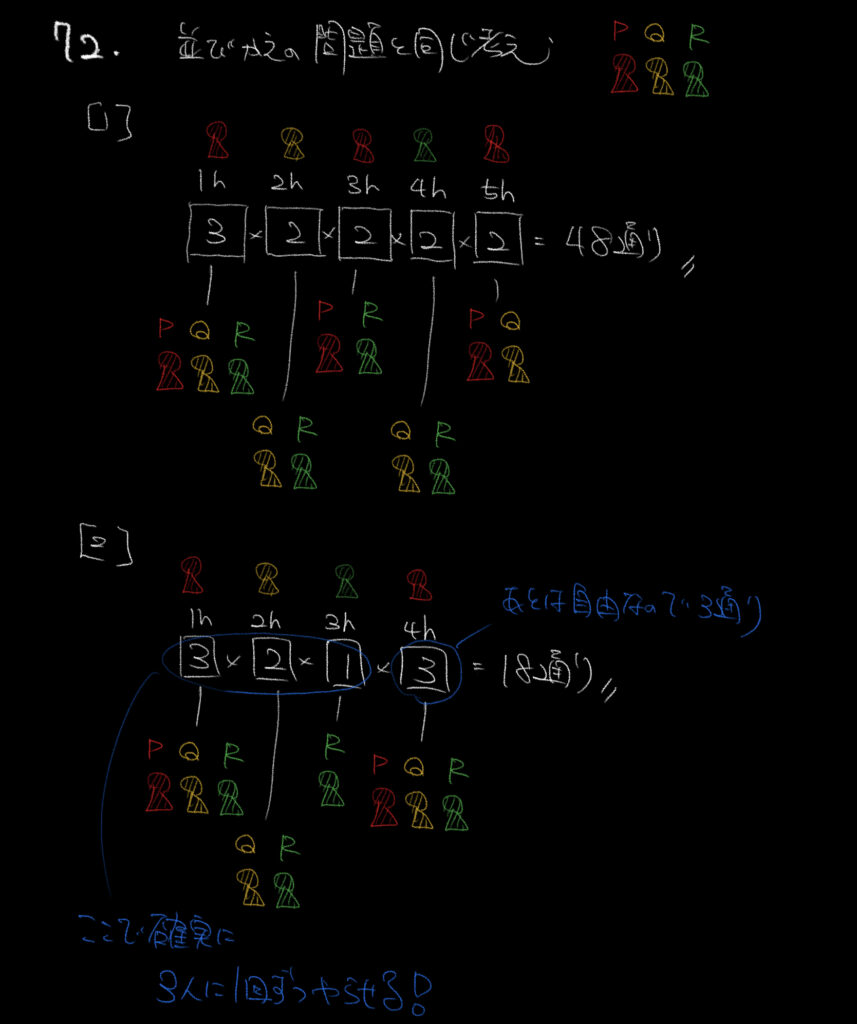

これもさっきと同じです。ボックスと並び替えの復習ですね。
これと同じです。はじめの1時間を決めると、次は2人、次も2人の繰り返しになることがわかります。
むしろトリッキーだったのは②の方でした。
②は最低1回はみんな当番をしなければいけなかったので、
最初の3時間で全員1回ずつ担当させることがポイントでした。
これで問題文の条件に当てはまりますね!
それが6通りで、最後の1時間は誰がやってもいいので3通り。
よって全部で18通りと求めることができます。


[73]問題に挑戦!
答えを見るにはここをクリック!
①30通り
②15通り
③4通り
[73]解説を見てみよう!


①この問題のポイントは7局目、6局目でした。
先に4勝した方が勝利なので7局目で必ず勝敗が分かれます。
というか、7局目まで試合が長引いているのなら、考えられる可能性は3対3のときだけです。
ここが分かれば、あとは簡単だと思います。
余事象で、全部の数から7局目までもつれ込んでしまう場合の数を引けばいいのです。
全体は35通り。7つのボックス(試合)に4回勝てばいいので7C44で求めることができます!
これがP、Qの2つの場合があるので35通り×2=70通りあります。
逆に3対3の時、6つのボックス(試合)に3回勝っている状況なので
20通りとなります。これもP、Qの2つの場合があるので20通り×2=40通りです。
これらの数字から、
70通り-40通り=30通りと求めることができます!
②は①の式で使ったものをそのまま使って計算してしまいましょう!
③は調べる作業が必要になってきますので、樹形図を使って解いていきましょう。
樹形図
樹形図とは簡単にいうと全部調べ上げちゃおう!て感じの解き方です。
そもそも、場合の数は時間が無限にあれば必ず解けます。
一個一個調べればいいわけですからね。ですが、そうもいきません。
テストには時間制限があります。
だから必死に楽しようと、公式を作って当てはめてみたり、いろいろズルをするわけです。
樹形図を書くとき、それは計算では複雑すぎて解けないときに行います。
極論計算でも求まる時もありますが、それだと逆に面倒!ってときに使う考え方です。


あくまで参考例なので、式でも解ける問題ですが、
上の問題のようにカードの並び方を樹形図で書くことができます。
今回の問題も3勝1敗の状態からなら、樹形図で書いた方が早いです。
Pがあと1勝したら終わり、負けてもあと1勝すれば終わり、という風に図にしていきましょう。
すると、最後の1通りだけQの逆転勝利になります。数えすぎにも気をつけましょうね。
まとめ
以上でこの単元は終了です!いかがでしたか?少しは解けるようになったでしょうか?
初めての解説だったのでかなり盛りだくさんでいろいろな知識を紹介しました。
覚えるのに時間がかかってしまうと思いますが、問題を解いていくことで徐々に慣らしていきましょう。
余事象、ボックス、樹形図をそれぞれどのようなときに使えばいいのか?
場合の数は本当に嫌いな人が多いので解くだけでも苦痛という方もいるかもしれませんが、行きたい企業があるのならもう少しだけ頑張ってみましょう!









