【中学受験攻略】樹形図を使って場合の数をマスターしよう！カードを並べてできる数の求め方

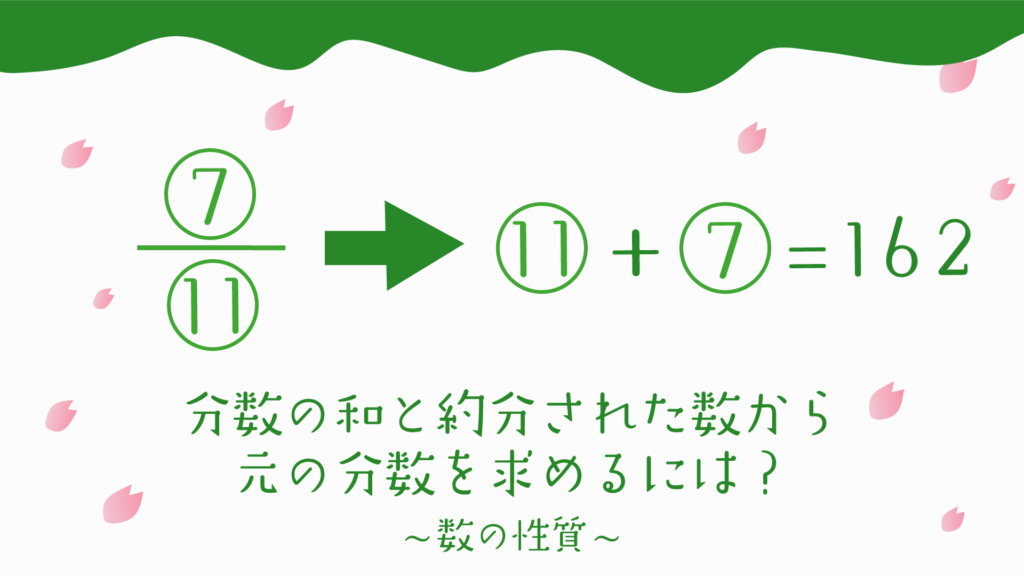
はじめに

今日は「 場合の数 」の問題の4問目です！
これまで「場合の数」の問題を3問解いてきましたね！
先に前の問題を解きたい受験生は下の記事をクリックしてみてください！
今日は樹形図について勉強していきましょう。

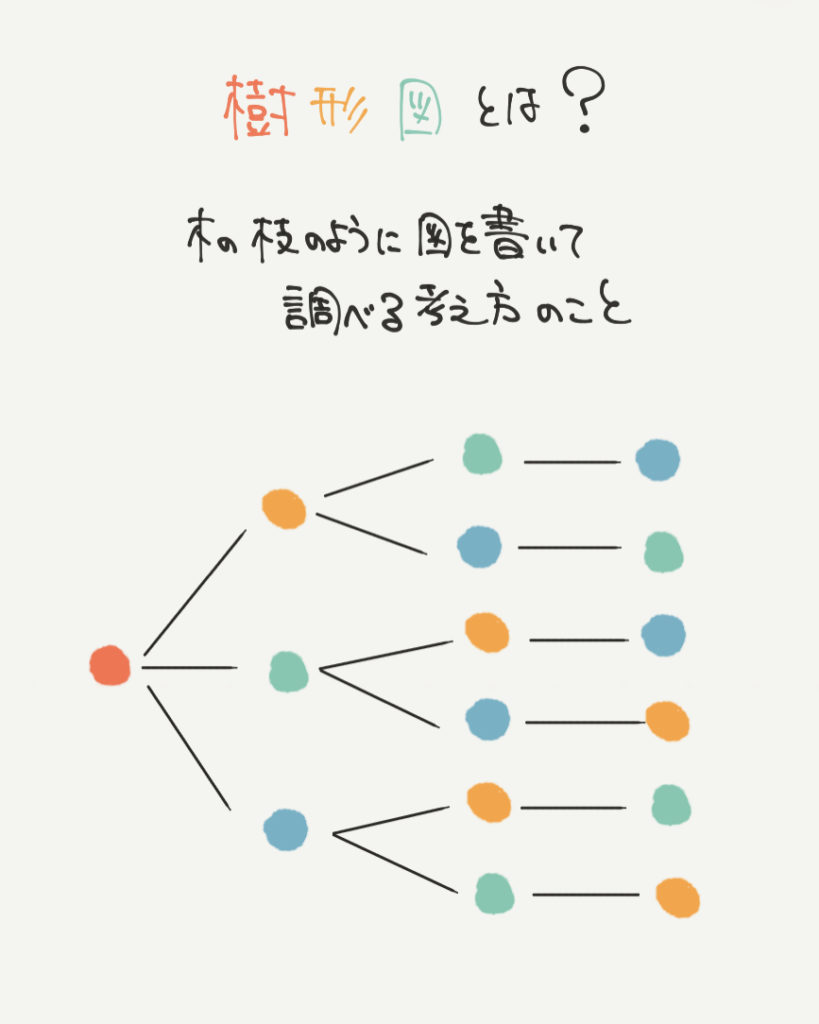
樹形図じゅけいずってなに？？

今回の問題では樹形図じゅけいずという言葉が出てきます。
樹形図じゅけいずとは、木から枝えだが生えるように線をのばしていく、場合の数の解き方です。

たとえば、4つの石●●●●を並べるとき、
●の石を先頭にして並べる場合の数は何通りあるかを数えたいとします。
そう考えると、樹形図じゅけいずを上のように書くことができます。
1番目が●でそこから枝えだのように石を増やして行きます。
すると●●●と並べることができ、そこからどんどん石を足して行きましょう。

「 場合の数 」の問題に挑戦ちょうせん！

表に0裏に2、表に0に裏に1、表に2裏に1と書いてある3枚のカードがあります。
この3枚を並べてできる3けたの整数は、全部で何通りですか。

解答

この記事を書いている人はこんな人

解説を読んで「 場合の数 」を攻略こうりゃくしよう！

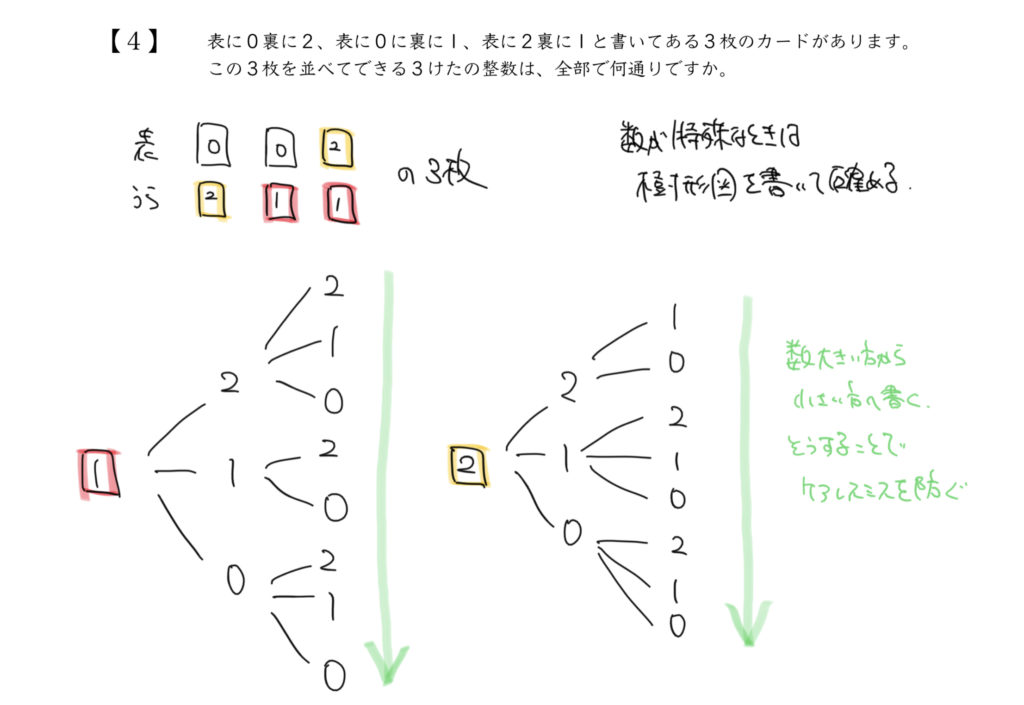
STEP1：問題文の内容を図にしよう

表の数や、裏の数がバラバラで、特別なので計算では求めることができません。

STEP2：百の位が1のときを考えよう

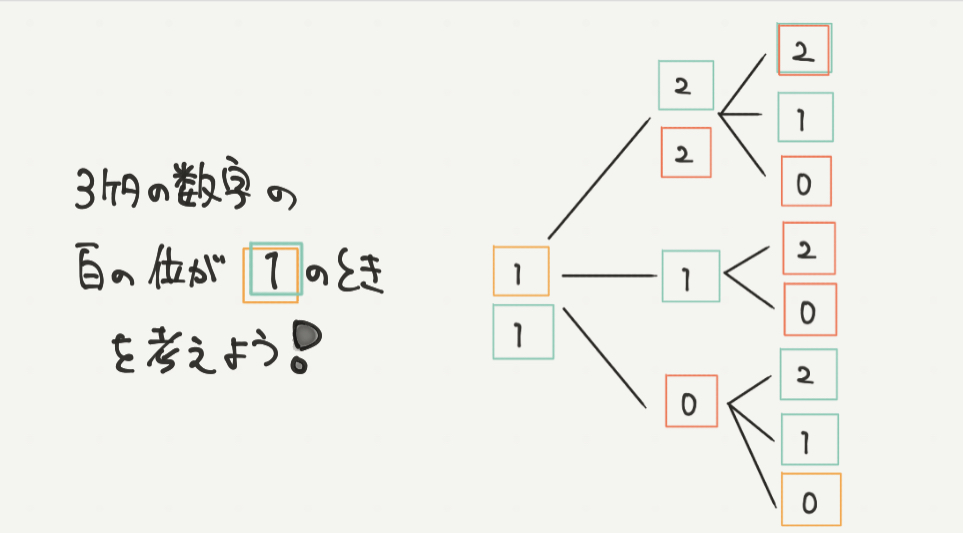
樹形図の書き方は上の図のとおりです。
数えわすれがないように、一の位は大きい数から小さい数になるように数えていきましょう。
すると百の位が1のときの場合の数は8通りあることがわかりました。

STEP3：百の位が2のときを考えよう

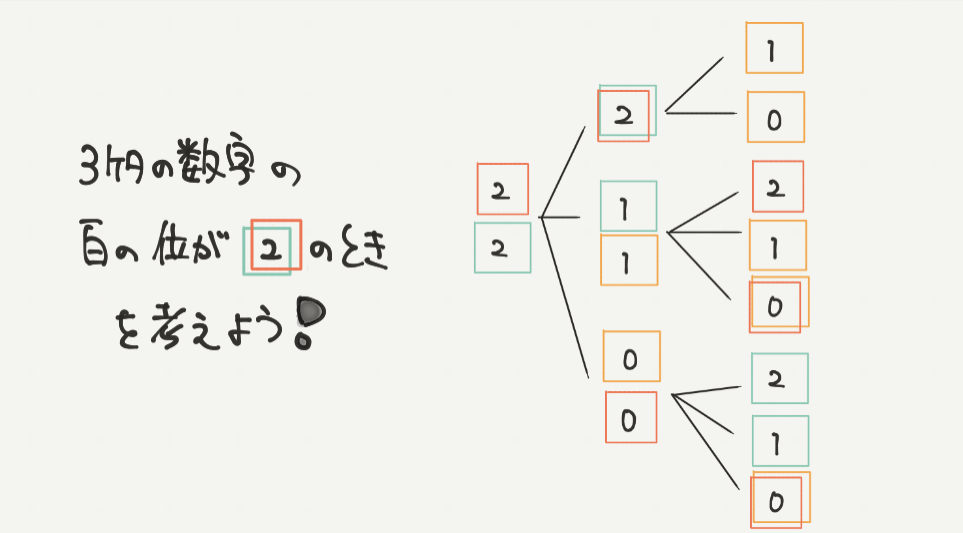
百の位が2のときも同じです。
上から順番に大きい数を書いていきましょう。
同じように計算すると場合の数がこちらも8通りあることはわかりますね。

STEP4：百の位が0の3けたの数字はない！

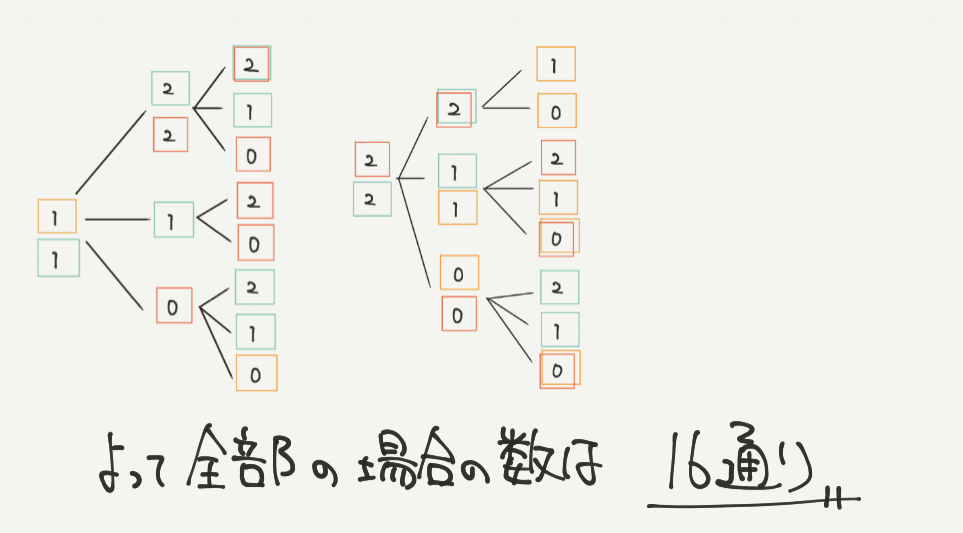
よって合計の数は8通り＋8通り＝16通りになります。

特別なカードを並べてできる数が何通りか求める問題のまとめ

「 場合の数 」の問題で大事なポイント

「 樹形図 」の考え方
・樹形図は枝のように線をどんどんのばしていって調べる考え方のことでした
樹形図の書き方の工夫
・樹形図を書くときは上から大きい数というふうに
　自分でルールを決めて書けるとミスなく数えることができます

以上で今日の問題は終わりです！
最後まで読んでくれてありがとうございました！！
次の問題で会いましょう！！！

その他の単元の問題の復習はこちらから！