目次
はじめに
今日は「 場合の数 」の問題の2問目です!
先に最初の問題を解きたい受験生は下の記事をクリックしてみてください!
あわせて読みたい


【中学受験攻略】場合の数をマスターしよう!画用紙の色分け問題を徹底解説!
【】 今日からチャレンジするのは「 場合の数 」の問題です!場合の数は苦手な生徒も多い印象です。私もとても苦手だったので一緒に頑張りましょう。まずはじめはヒント…
「 場合の数 」の問題に挑戦!
解答
答えを見るにはここをクリック!
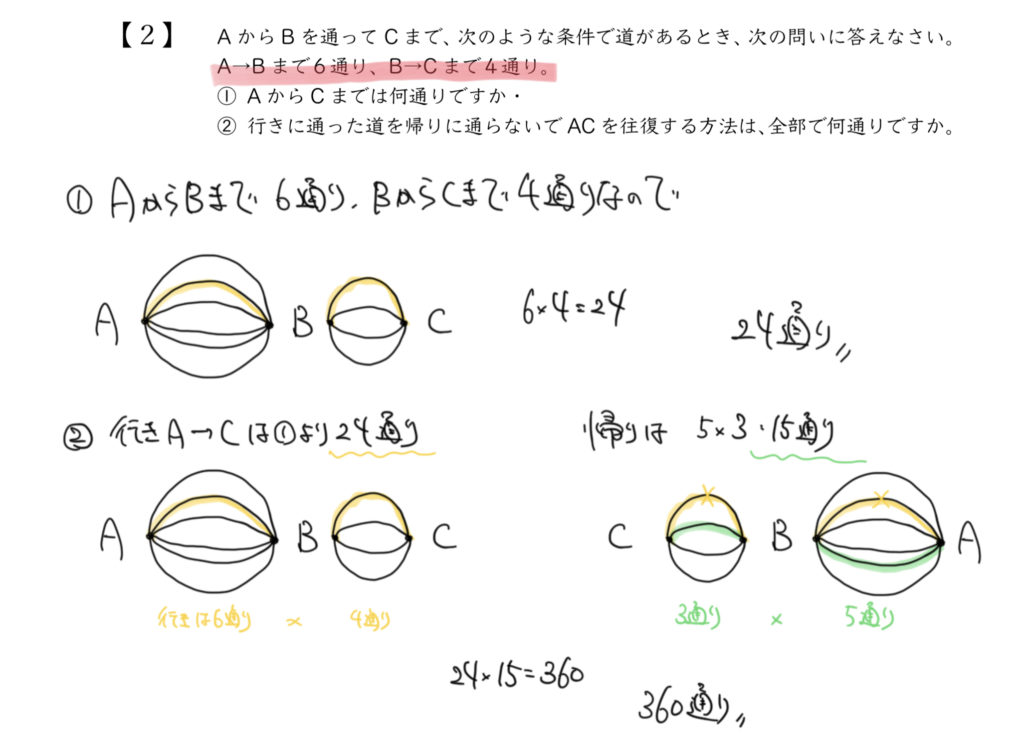
①24通り
②360通り
この記事を書いている人はこんな人

解説を読んで「 場合の数 」を攻略しよう!
STEP1:問題文を図になおそう
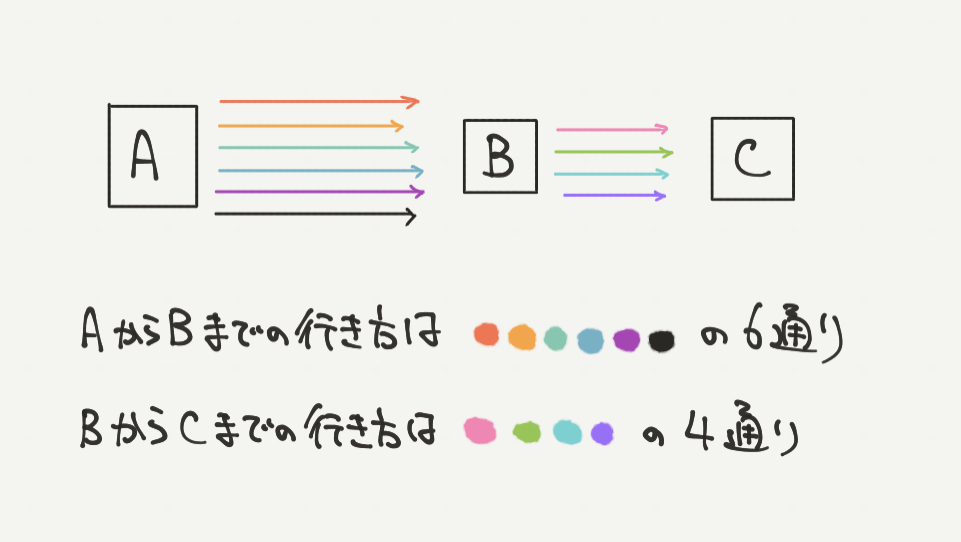
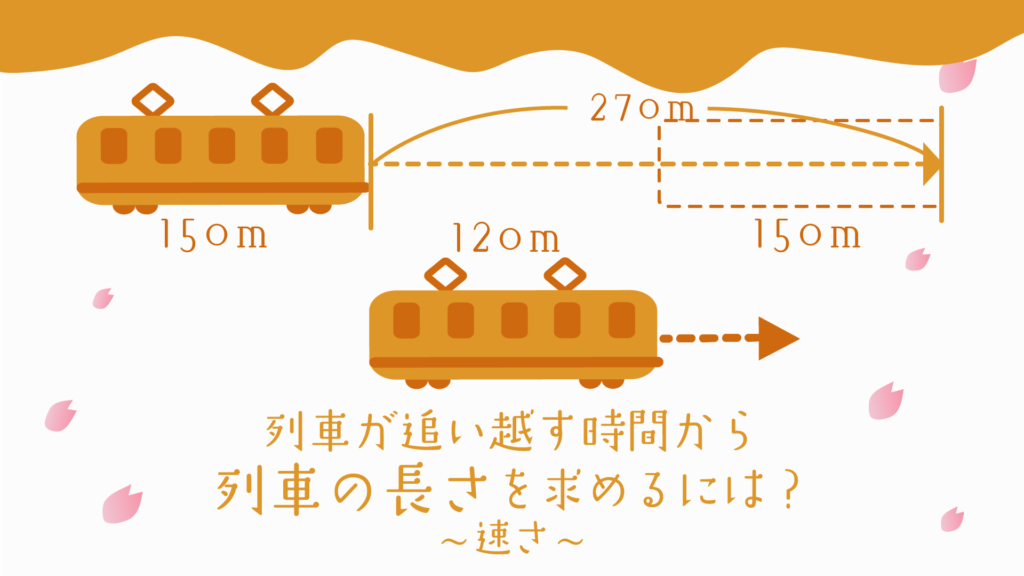
問題文の情報を図にするとこのようになります。
①しっかりと図をかけば、組み合わせを求めることができますので落ちついて書いてみて下さい。
AからBへの行き方は→→→→→→の6通りあります。
BからCへの行き方は→→→→の4通りあります。
STEP2:たとえばA→Bのとき!
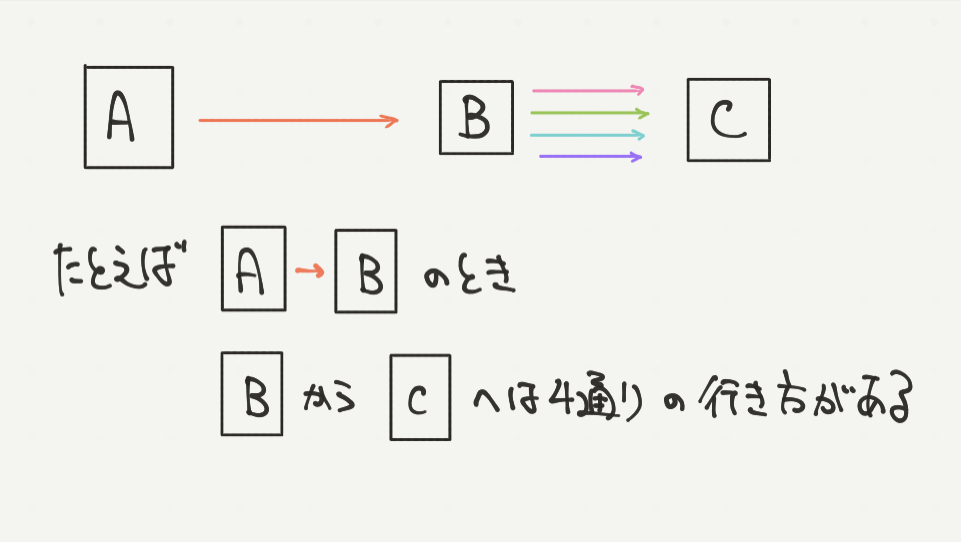
たとえばA→Bのときを考えてみましょう。
A→Bで進むとき、BからCへの行き方は→→→→の4通りあります。
同じように、A→B、A→B、A→B、A→B、A→Bのときも考えてみましょう。
STEP3:4通りの行き方×6で考える
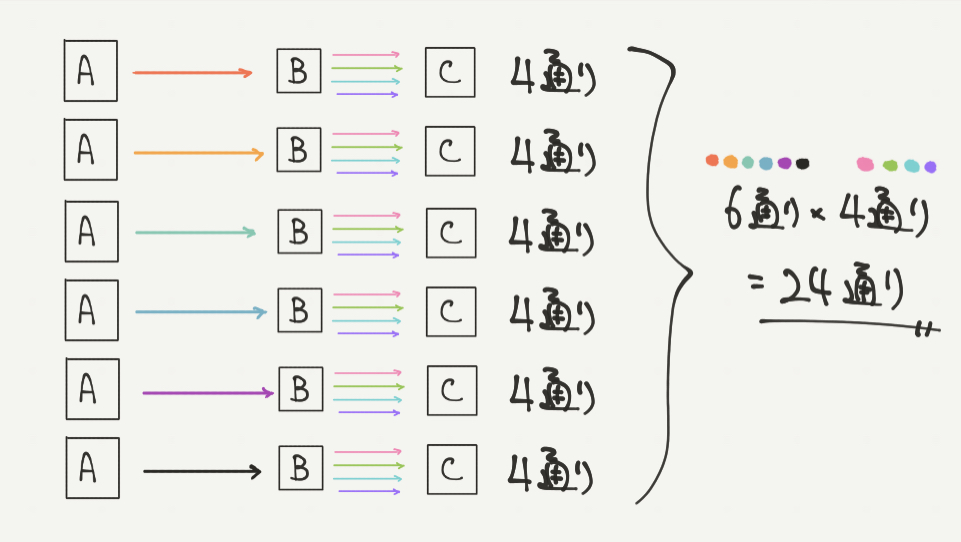
このように図で表すと考えやすいと思います。
図のように、A→B、A→B、A→B、A→B、A→B、A→Bの
6通りのパターンにそれぞれ4通りの行き方がありますので、
6×4=24通りで答えが求まります。
STEP4:帰りは行きに使った道は通れない
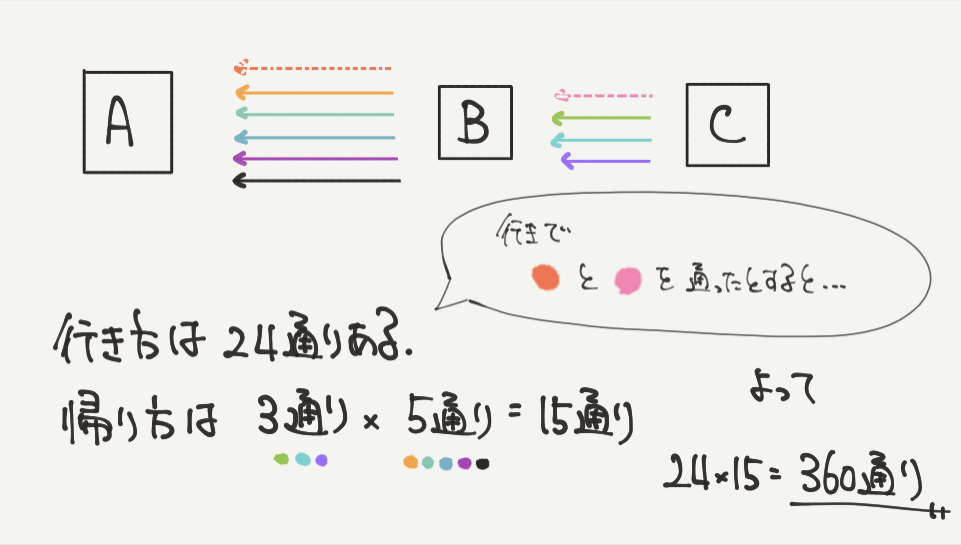
②行きに使った道は使えないので、帰りは別の道を通って帰ります。
それぞれ帰りの道が1本ずつ使えないのがポイントです。
たとえば、行きにA→B→Cの道順でCまで向かったとします。
すると帰りの道は、
CからBへの行き方は→→→の3通りになりますね。
同じようにBからAへの行き方は→→→→→の5通りあります。
よって行きの道とちがう道で往復する方法は、
6×4×5×3=360通りと計算することができました。
道を往復する方法が何通りあるのかを求める問題のまとめ
「 場合の数 」の問題で大事なポイント
「 場合の数 」の考え方
・A→Bの行き方×B→Cの行き方で計算しよう
「仮定」の考え方
・仮定とは?もし○○が□□だったら〜と考える方法でした
・今回はもし行きに赤の道、ピンクの道を通ったら・・・と考えましたね
以上で今日の問題は終わりです!
最後まで読んでくれてありがとうございました!!
次の問題で会いましょう!!!