はじめに
今日は「 場合の数 」の問題の3問目です!
これまで「場合の数」の問題を2問解いてきましたね!
先に最初の問題を解きたい受験生は下の記事をクリックしてみてください!

「 場合の数 」の問題に挑戦!
解答
答えを見るにはここをクリック!
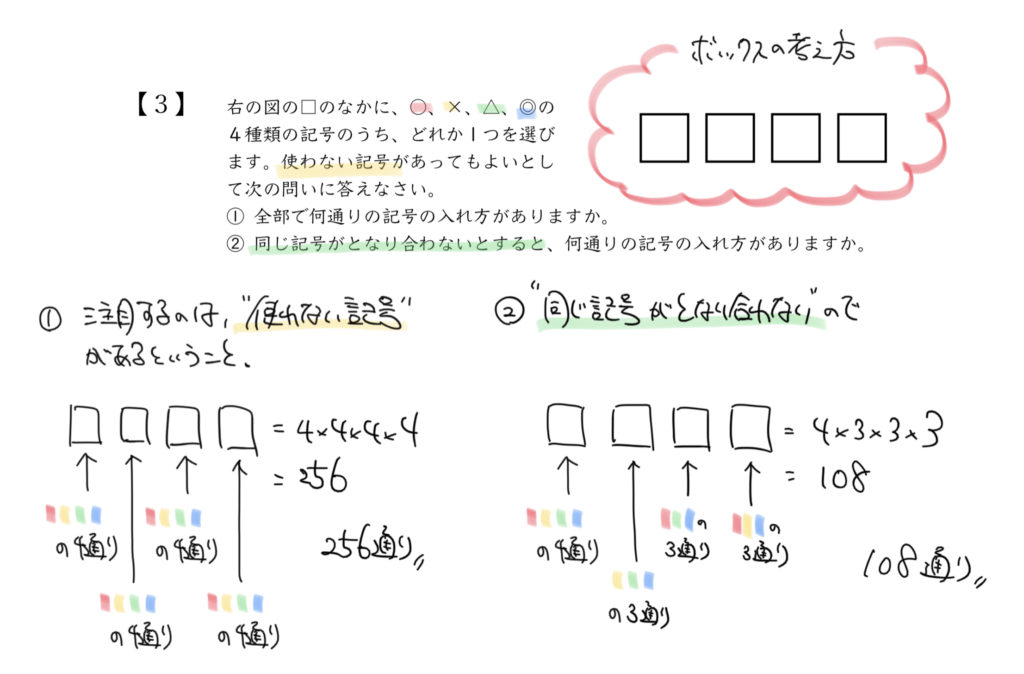
①256通り
②108通り
この記事を書いている人はこんな人


解説を読んで「 場合の数 」を攻略しよう!
STEP1:使わない記号があるときはかんたん!
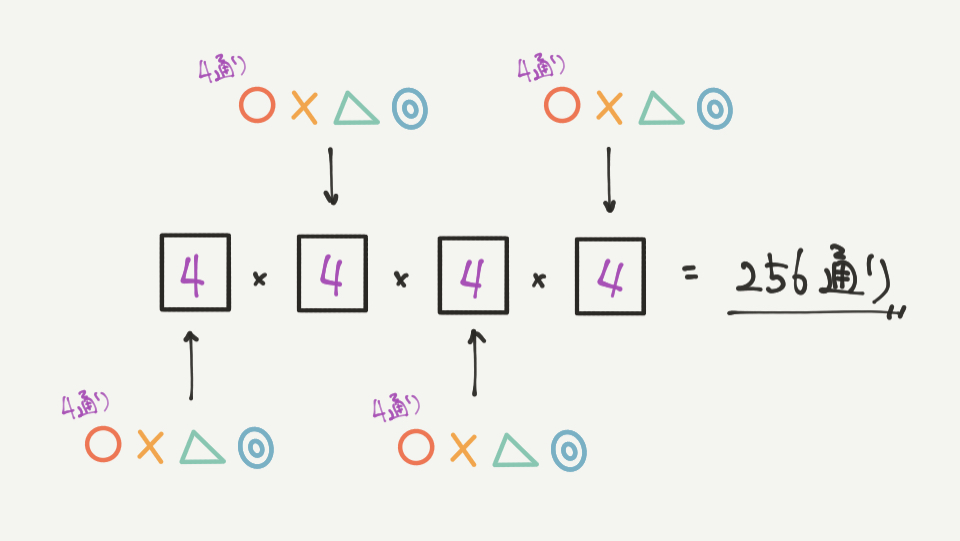
今回のポイントは“使わない記号がある”ということです。
①の問題ではどの□に何を入れても関係ありません。
なぜなら、「となりとちがう記号を入れなさい」とか「全部の記号を使いなさい」と言われていないからです。
 わかみや先生
わかみや先生どのマスに何を入れてもいいってことなんですね!
前の記事で解いた色のぬり分け問題はとなり合う色を別にしないといけないので、
考えないといけないことがいくつかありました。
今回は何回でも同じ記号を使ってもいいので、4×4×4×4=256通りと求まります。
STEP2:となりと同じ記号にならないためには?
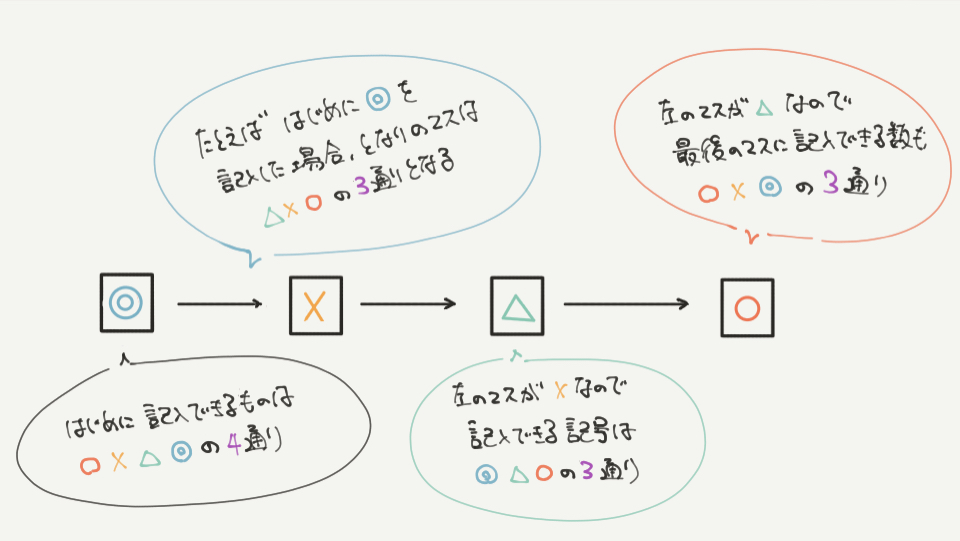

②の問題ではとなりと同じ記号にならないための場合の数を求めて行きます。
一番左のマス:どんな記号も入れられるので4通り
→たとえば◎を入れて、◎□□□になったとします。
次のマス:◎を入れてしまうととなり合ってしまう(◎◎□□)ので◎以外の3通り
→たとえば、×を入れて、◎×□□になったとします。
次のマス:×を入れてしまうととなり合ってしまう(◎××□)ので×以外の3通り
→たとえば、△を入れて、◎×△□になったとします。
最後のマス:△を入れてしまうととなり合ってしまう(◎×△△)ので△以外の3通り
→たとえば、○を入れて、◎×△○を作ることができました。
STEP3:場合の数を整理してみよう
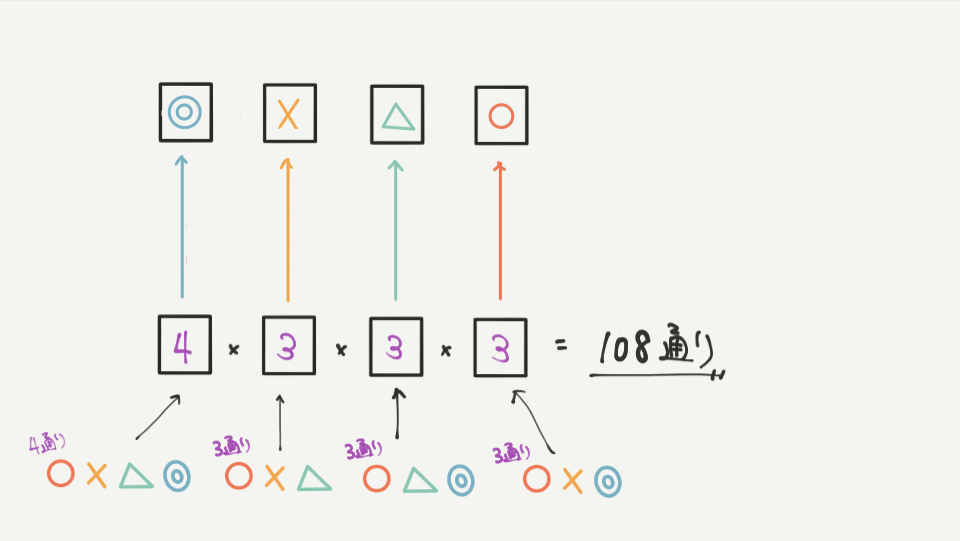

STEP2の内容をまとめると、
はじめの□には4通り、
次の□にはとなり同士にならないように3通り、
次もとなりと違う記号なので3通り、
という風に計算することができます。
よって答えは4×3×3×3=108通りとなります!!
4種類の記号を並べる方法が何通りあるのかを求める問題のまとめ
「 場合の数 」の問題で大事なポイント
「 場合の数 」の考え方
・□に入ることができる記号が何通りかを考えましょう
「となり合ってはいけないとき」の考え方
・前の記号を入れてはいけないので、別の記号を入れないといけませんでした
「仮定するとき」の考え方
・もし○○が□□だったら〜と考えるやり方
・今回はもし一番左のマスに◎が入ったら〜と考えていきましたね
以上で今日の問題は終わりです!
最後まで読んでくれてありがとうございました!!
次の問題で会いましょう!!!