はじめに
今日は「 場合の数 」の問題の5問目です!
これまで「場合の数」の問題を4問解いてきましたね!
前の問題を解きたい受験生は下の記事をクリックしてみてください!

「 場合の数 」の問題に挑戦!
解答
答えを見るにはここをクリック!
56通り
この記事を書いている人はこんな人


解説を読んで「 場合の数 」を攻略しよう!
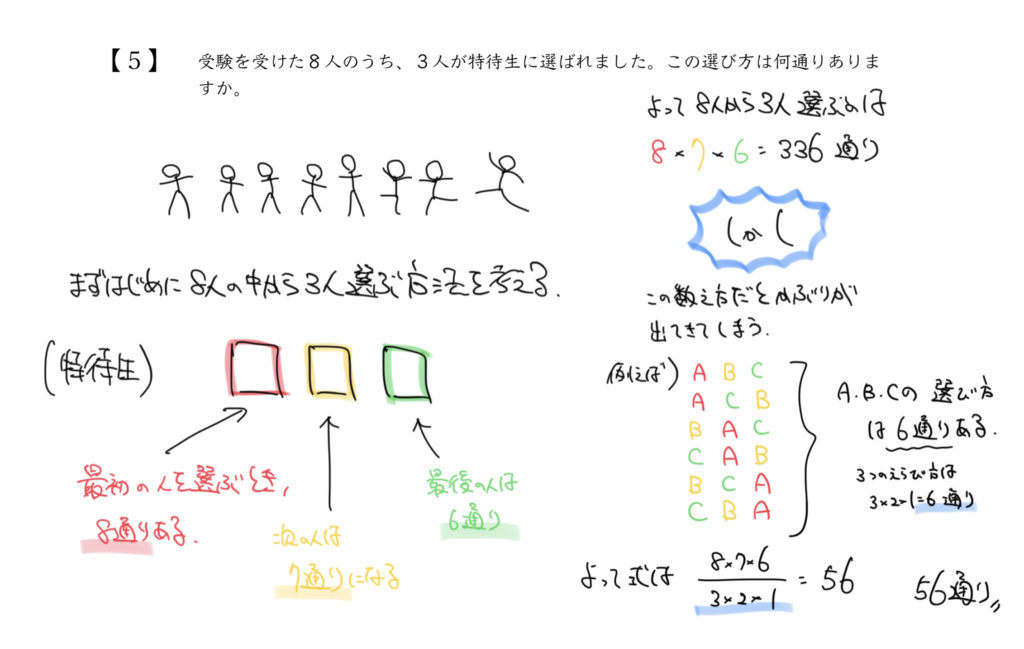
STEP1:問題文の内容を図にしましょう
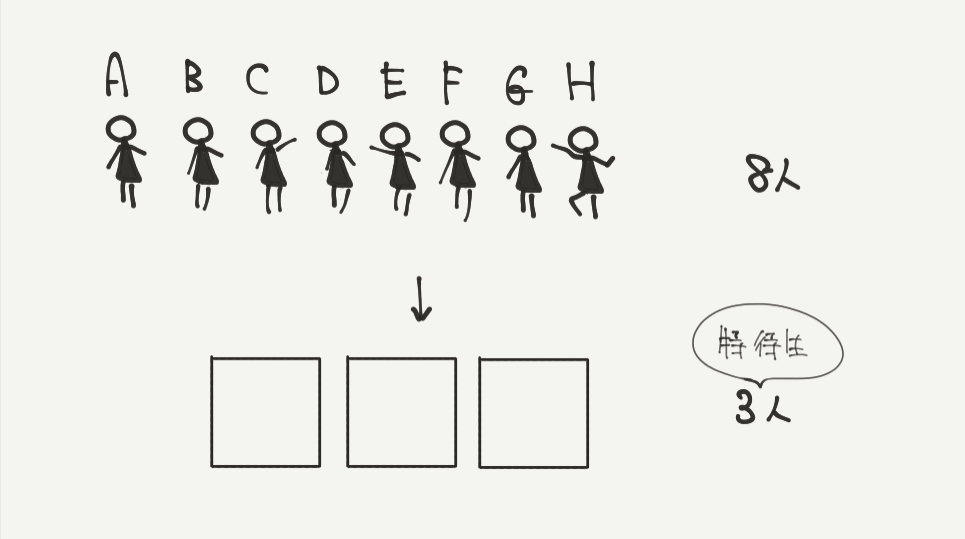
いつも通り、まずやることは問題文を図に直すことです。
8人の生徒の中から特待生を3人選ぶ方法について、計算してみましょう。
STEP2:8人から3人を選んでみよう!
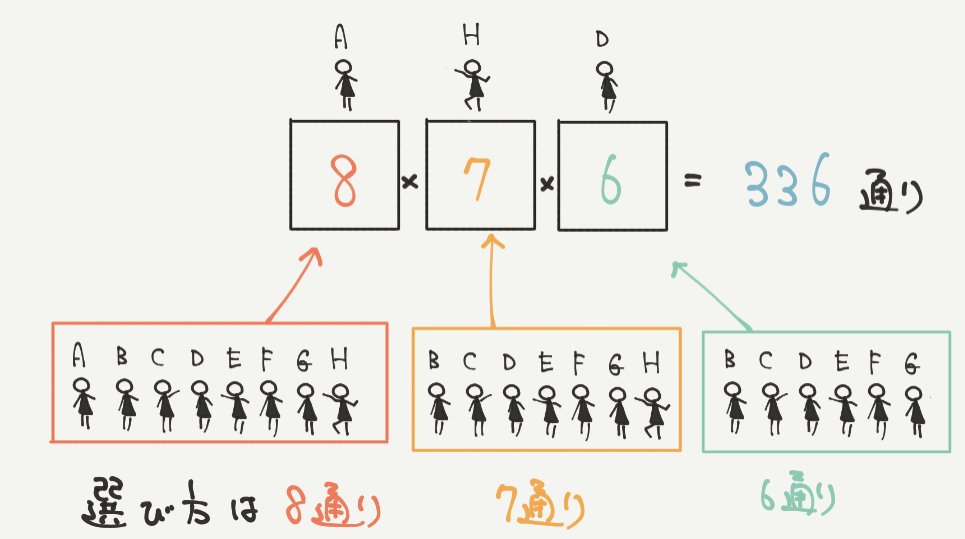
ふつうに解いてみましょう。
するとはじめの特待生に選ばれる生徒が8人いるので、8通りとなります。
ここでたとえばAさんが選ばれたとします。
次に2番目に選ばれる生徒はAさん以外の7人になります。
ここでHさんが選ばれたとすると、
最後に選ばれる人はAさんとHさん以外の6人になります。
なので、8×7×6=336通りと答えを出してしまいますが、それはまちがいなので注意です。
なぜなら今回の問題では並べているのではなく、選んでいるからです。
STEP3:選び方と並べ方のちがいに気をつけよう
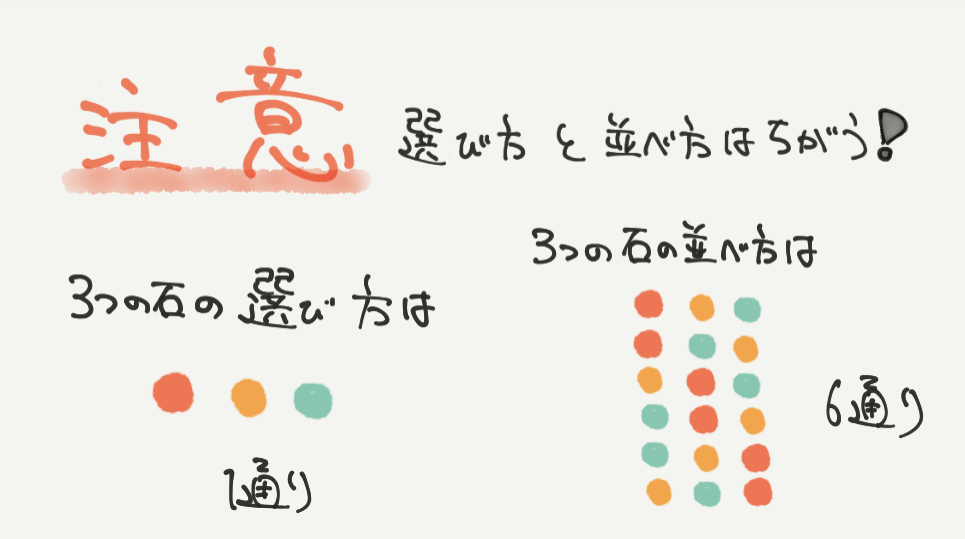
ここで、選び方と並べ方のちがいについて考えてみましょう。
たとえば3つの石●●●を選ぶとします。
すると●●●の順番で選んでも、●●●の順番で選んでも選ばれる石は1通りになります。
ですが、3つの石●●●の並べ方は、
●●●
●●●
●●●
●●●
●●●
●●●
の6通りです。
なので、3つの石を選ぶときと並べるときでは1通りと6通りとかなりの差があることがわかります。
STEP4:かぶりを考えて計算しよう
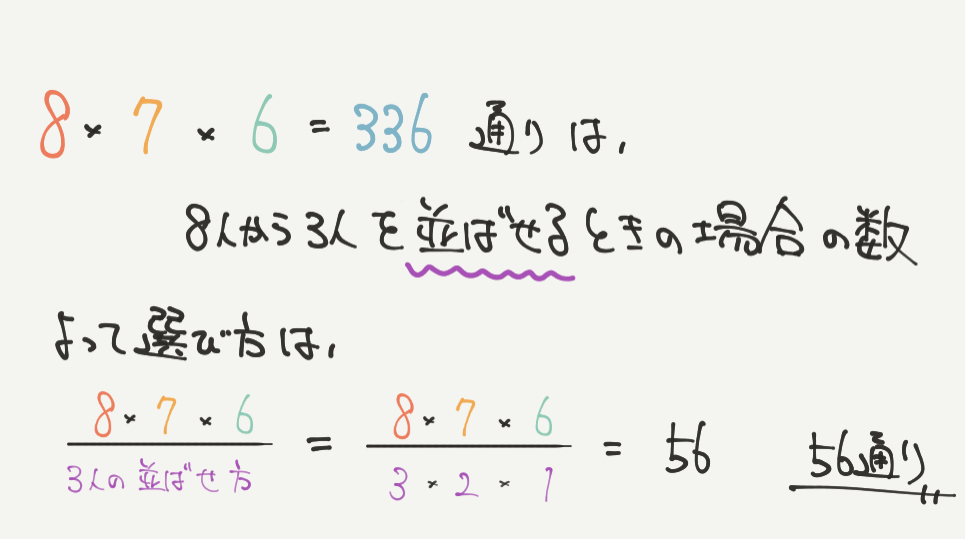
8人から3人選んだつもりになっている8×7×6=336は、
実は8人から3人を並ばせるときの場合の数になります。
つまり8×7×6=336には、3×2×1=6通りだけのかぶりがあるということです。
なので全体の336通りから6を割って答えである56通りと求めます。
8人の生徒から3人の特待生を選ぶ場合の数を求める問題のまとめ
「 場合の数 」の問題で大事なポイント
「 かぶり 」の考え方
・選ぶときと並べるときは別で考えないといけません
・選ぶとき:AとBでもBとAも同じ!
・並べるとき:ABとBAはちがう!!
以上で今日の問題は終わりです!
最後まで読んでくれてありがとうございました!!
次の問題で会いましょう!!!