【中学受験攻略】図で学ぶ推理問題のコツ！筆算を読み解いて□にあてはまる数字を求める問題

はじめに

「 調べと推理 」の問題の6問目にチャレンジしましょう〜！
これまで5問の問題を解いてきました！
事前に復習したい受験生はまずはこちらからチャレンジしてみましょう。

「 調べと推理 」の問題に挑戦ちょうせん！

下の足し算の計算の□に当てはまるように0以上9以下の整数を求めなさい。

解答

この記事を書いている人はこんな人

解説を読んで「 調べと推理 」を攻略こうりゃくしよう！

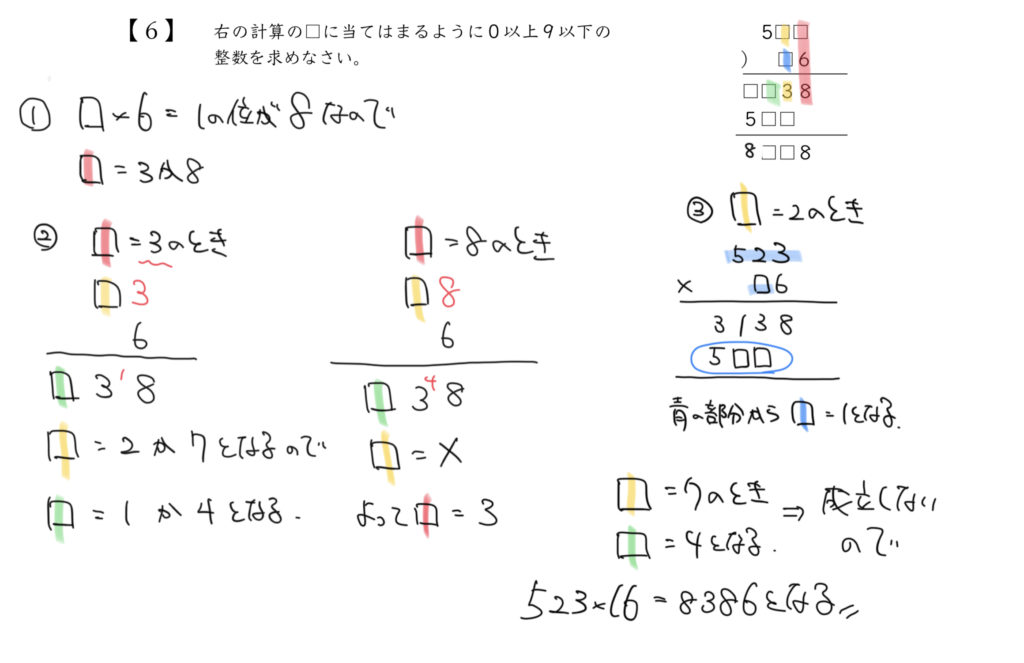
STEP1：6×□＝1の位が8になる数を探そう！

赤色のかけ算に注目してみましょう。
すると□×6の1の位が8になるので、
□に当てはまる数は3か8になります。

この2パターンについて調べてみましょう。
必ずどちらかにおかしなところがあるはずです！！

STEP2：□＝3のとき、□に入る数を調べあげよう！

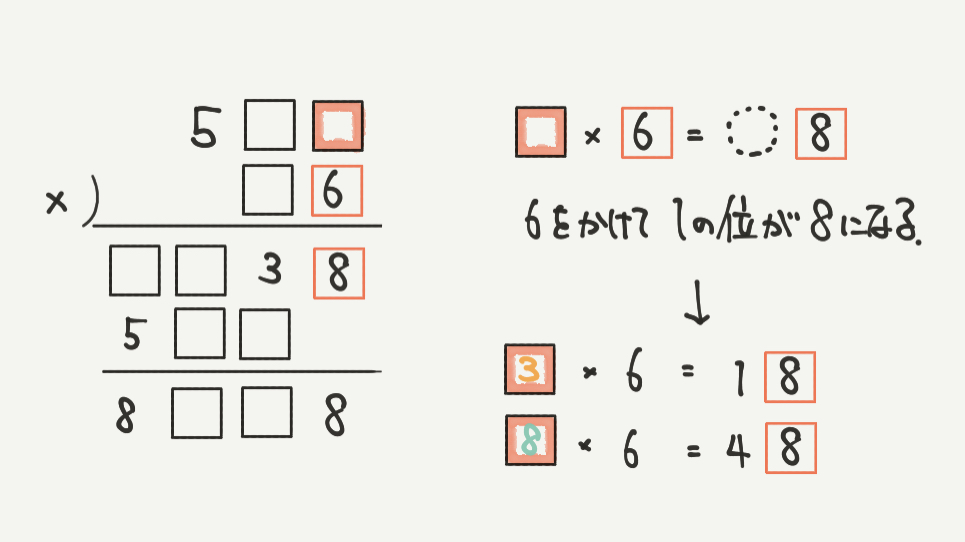
□が3のときを調べてみましょう。
すると、□3×6＝□38なので、□×6＝2である数を調べます。

□3×6をすると、3×6＝18で、十の位に1が足されていますね。
なので、□×6＝2と考えることができます。

このとき、□＝2の場合か□＝7の場合が考えられます。
ひとまずここまででおかしなところがないことが確認できました。

続いて□＝8のときを調べてみましょう。

STEP3：□＝8のとき、□に入る数を調べあげよう！

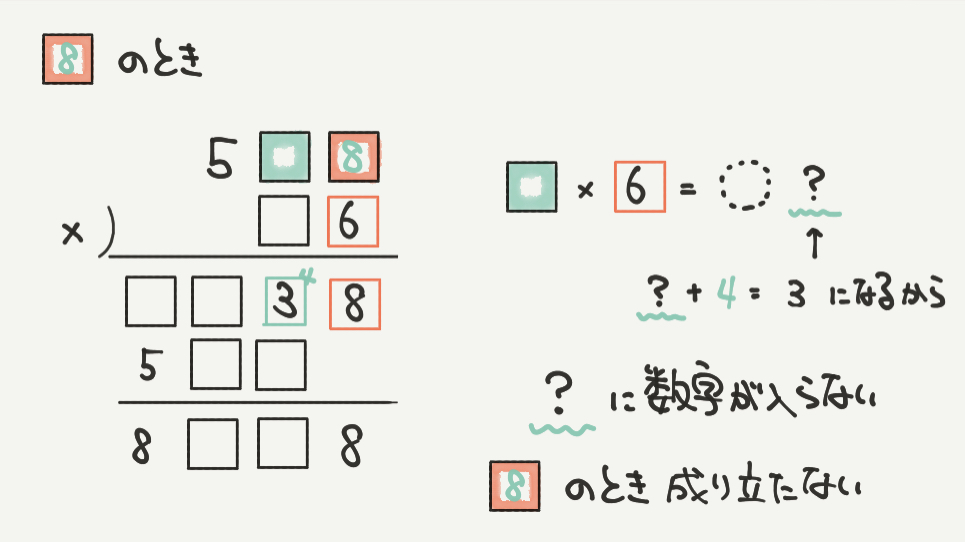
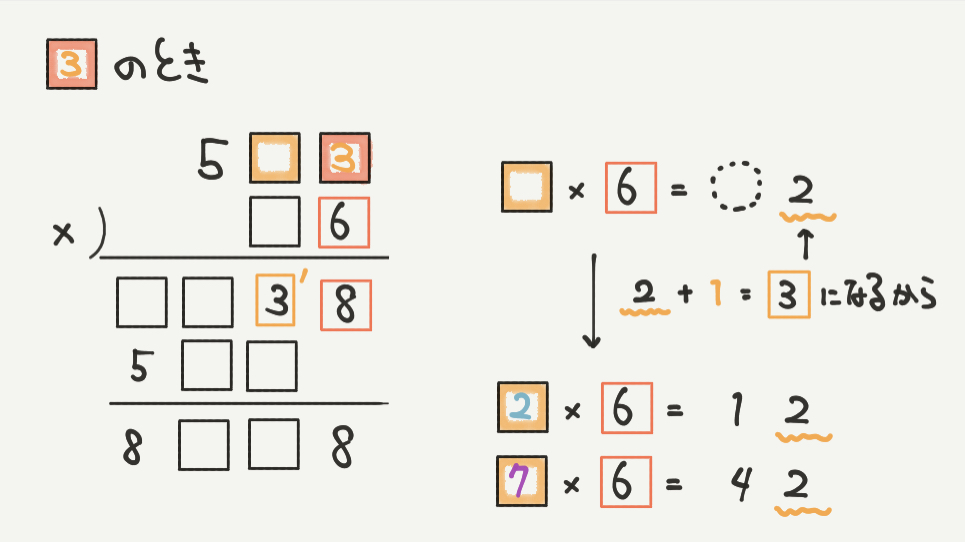
□＝8のとき、十の位がおかしくなります。
□×6＝？となってしまい、当てはまる数がなくなってしまいます。
ですので□＝8ではなくSTEP2で解いた□＝3であることが確定します。

STEP4：□＝3のときと□＝2のとき、残りの□を調べてみよう！

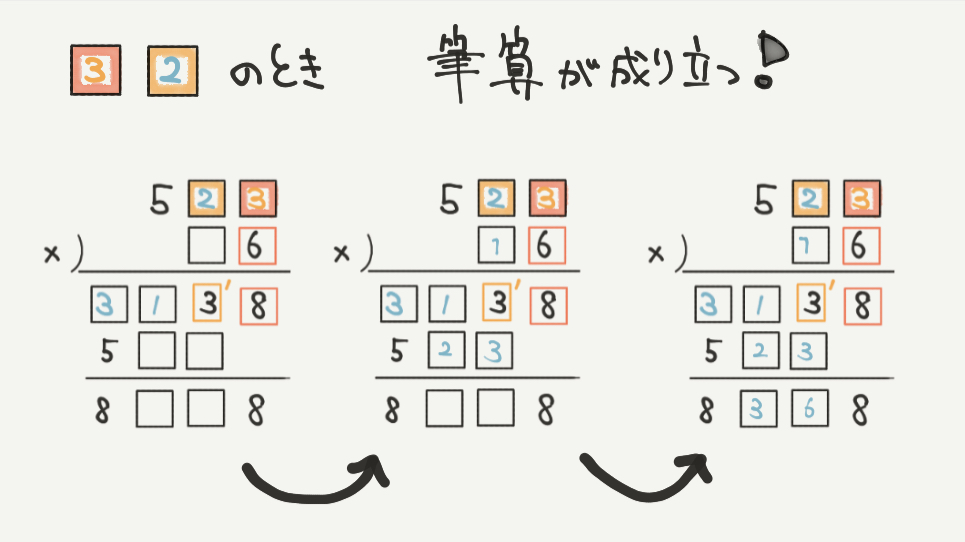
□が2のとき、残りの□を書いていくと上図のようになりきれいに筆算の式を書くことができます。

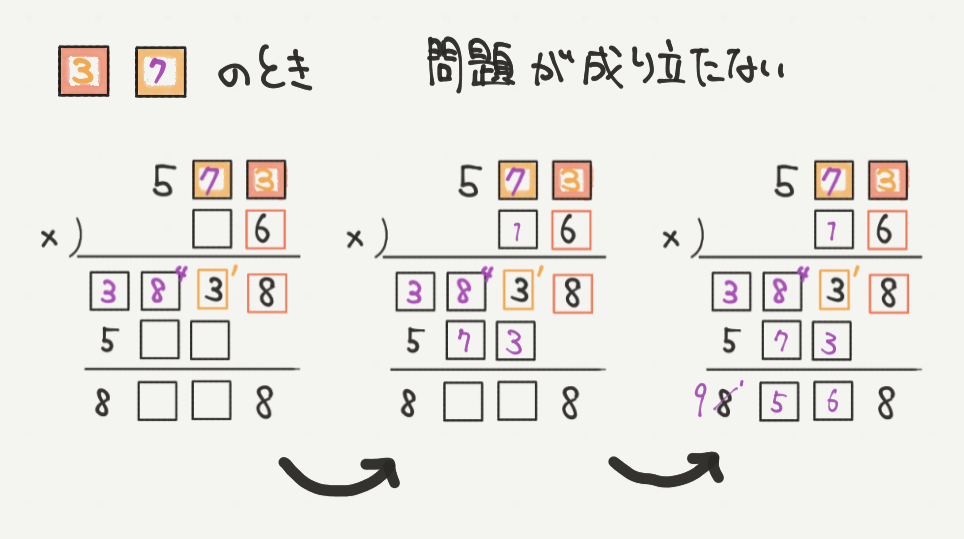
一方で□が7のとき、筆算の式の千の位の数が成り立たなくなってしまいます。

よってこの式だとおかしくなってしまうので、
□が2であることがわかりました。

答えは523×16=8368となりました！！

計算式の◻️に当てはまる数字を求める問題のまとめ

「 調べと推理 」の問題で大事なポイント

「 推理算 」の考え方
・分かっている情報を書きこむ
・数の性質を使ってわかるところを1つずつ書く
確定しない数は場合わけで考える
・今回はSTEP1,2,3で3か8で場合分けしましたね！
・STEP4では2か7で場合分けしました！

以上で今日の問題は終わりです！
最後まで読んでくれてありがとうございました！！
次の問題で会いましょう！！

その他の単元の問題の復習はこちらから！