はじめに
みなさんこんにちは!
今回はみなさんもよく知っている年令についての問題です。
「年令算」と呼ばれたりするらしいです。(覚えなくてOK!)
全ての受験生にわかるように、ていねいに解説をしているので諦めずに頑張りましょう!
それではまずはカンタンなウォーミングアップから始めていきましょう。
年令算の考え方
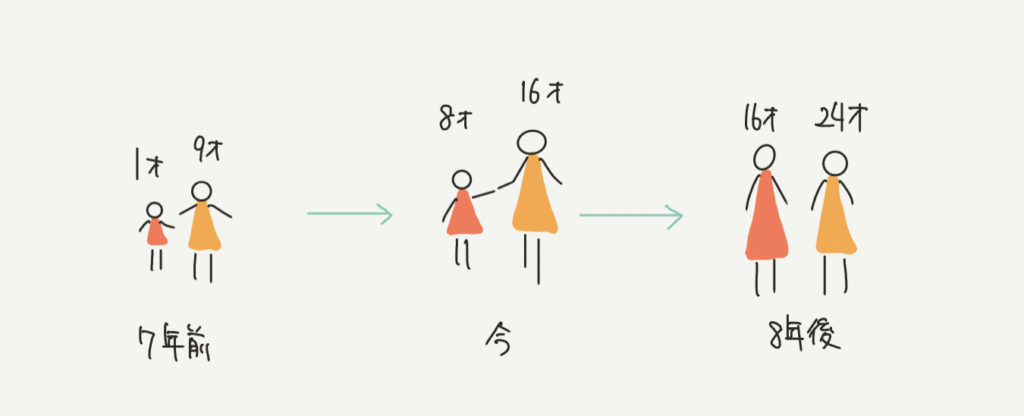
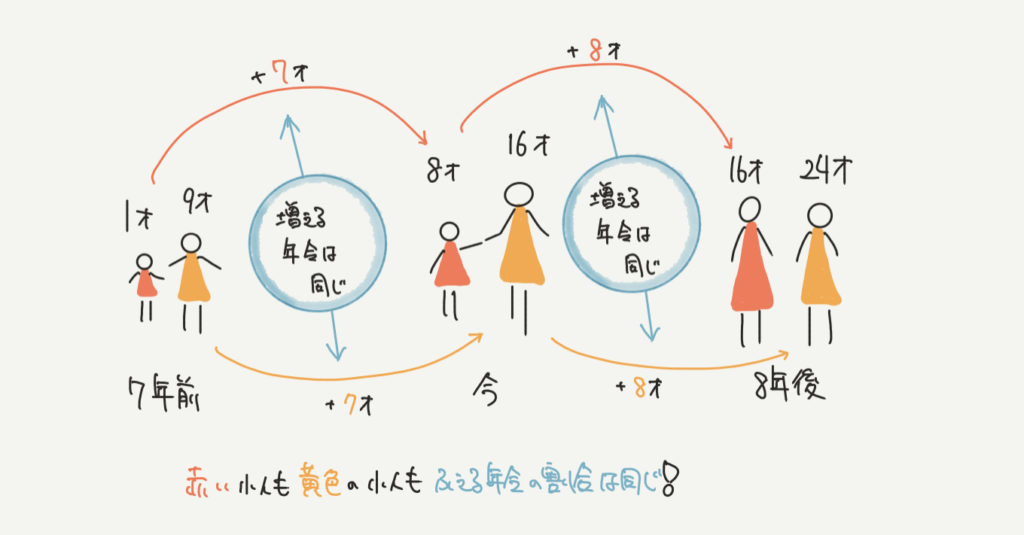
今、8才の赤い小人と16才の黄色い小人がいるとします。
この2人の7年前、8年後の年令はいくつですか?と聞かれたらすぐに
7年前→赤い小人1才、黄色い小人9才
8年後→赤い小人16才、黄色い小人24才
と求めることができると思います。
では、黄色の小人の年令は赤い小人の何倍ですか、と聞かれたらどうしますか?
その場合、線分図を書いて見るとわかりやすく考えることができます。
では実際に書いてみましょう。
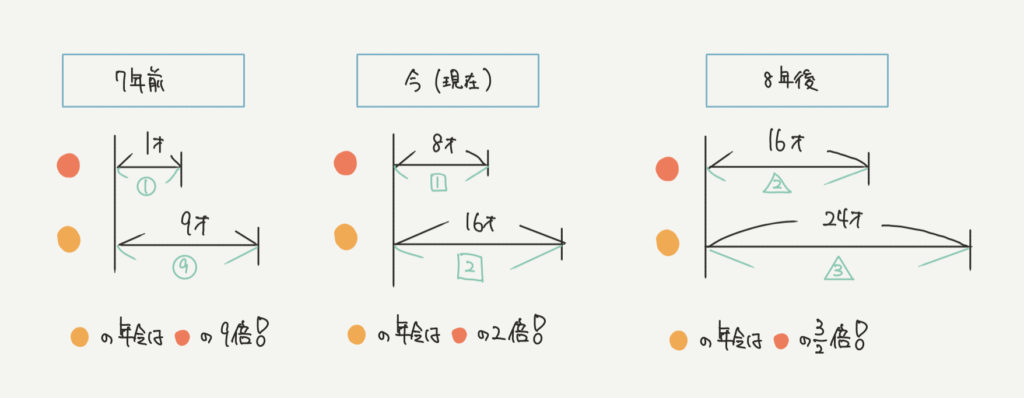
赤いまるが赤い小人の年令、黄色いまるが黄色い小人の年令を表しています。
線分図を見てみよう(7年前の2人の年令)
まずは7年前の図に注目すると、赤い小人が1才、黄色い小人が9才であることがわかります。
ここで赤い小人の年令を①とすると、
黄色い小人の年令は当然⑨と表すことができますね。
なので、黄色い小人の年令は赤い小人の9倍であることがわかります。
線分図を見てみよう(現在の2人の年令)
では現在の2人の年令を見てみましょう。
赤い小人は8才、黄色い小人は16才なので、
赤い小人の年令を①とすると黄色い小人の年令は②になりますね!
なので、黄色い小人の年令は赤い小人の2倍であることがわかります。
線分図を見てみよう(8年後の2人の年令)
それでは最後に8年後の2人の年令を見てみましょう。
赤い小人は16才、黄色い小人は24才なので、
赤い小人の年令を②とすると黄色い小人の年令は③になることがわかります。
 わかみや先生
わかみや先生赤い小人の年令を①にすると、黄色い小人の年令が
小数になってしまうので、今回は②で考えよましょう!
よって、黄色い小人の年令は赤い小人の3/2(1.5)倍であることがわかります。
ここまで理解できたら実践問題に挑戦していきましょう!
問題に挑戦!
解答
答えを見るにはここをクリック!
6年前
この記事を書いている人はこんな人


解説を見てみよう!

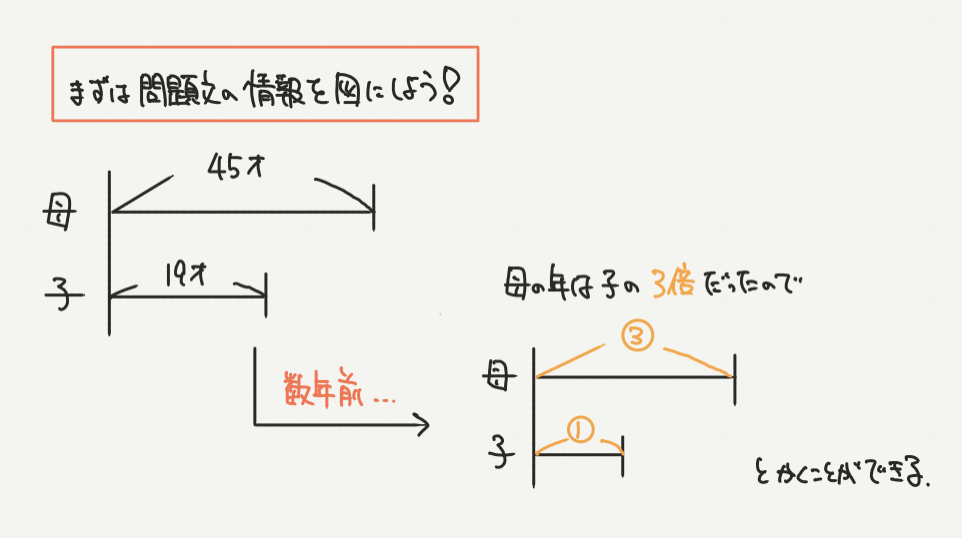
STEP1:まずは問題文を図にしよう!

まずは問題文をきちんと図にするところから始めましょう!
ここをまちがえてしまうと、ほかの計算があっていても不正解になってしまいます。
この最初のステップ(STEP1)をみて、自分の書いた図が正しいかどうかをチェックしましょう。
今、母の年令は45才で子供が19才なので、左の線分図がかけると思います。
そして数年前には母の年令は子供の3倍だったそうなので、
数年前の子供の年令を①とすると、母の年令は③とあわらすことができると思います。
ここまでかけたらSTEP2に進みましょう!
STEP2:同じところを見つける作る!
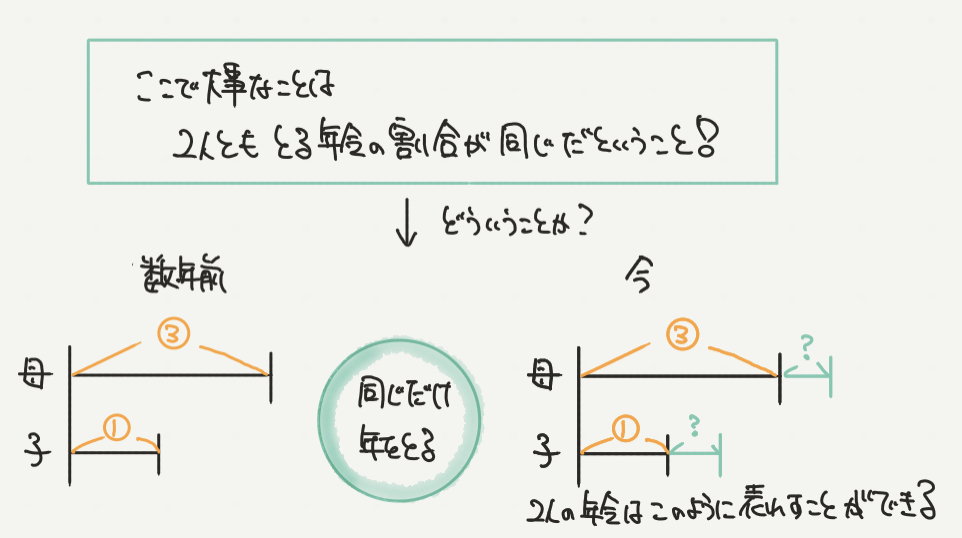

STEP2では数年前と今の線分図から追加で書けることを書いていきます。
ここで大事になってくるポイントが同じところを見つけることです。
この問題の一番大切なポイントがこのSTEP2の考え方です!!
いきますよ?よく見て理解してくださいね!
数年前と今の年令で2人のとった年は必ず同じ、です!
どういうことかというと、
数年前から今の年令で例えば母親が3才年をとったとしたら、
子供も必ず3才分年をとるはず、ということです。当たり前ですよね?
この当たり前の情報を緑で書き込んでみると、
今の年令の線分図を
母:③+?
子:①+?
と書くことができると思います。
(?は数年前から今まででとった年の数)
ここまでがSTEP2です!さあ、あともう少しです〜!
STEP3:今の2人の年令の線分図に情報を書き足そう!
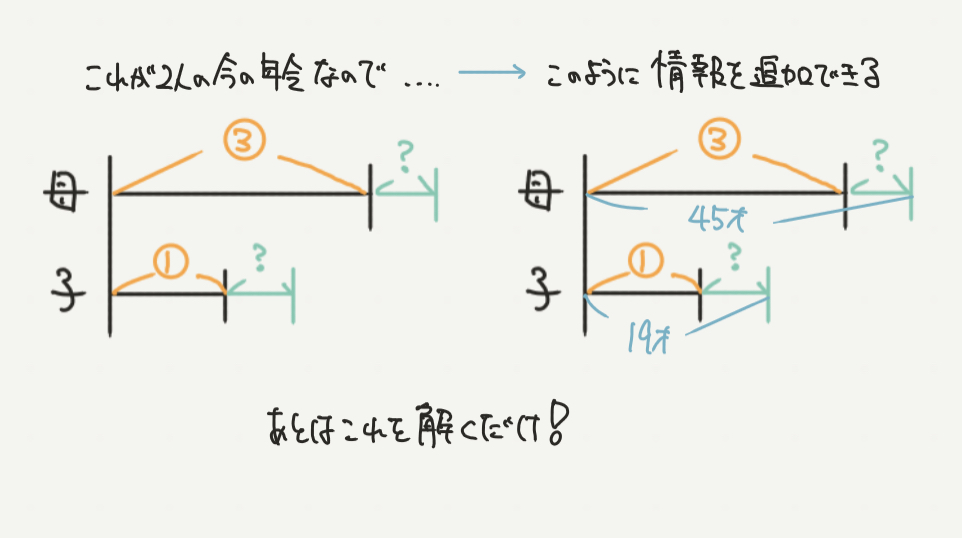

さて、STEP2でわかったことは、
母:③+?=45才
子:①+?=19才
でしたね!
(?は数年前から今まででとった年の数)
これを線分図に書き足していくと青のところがわかると思います。
あとは、計算して?を求めてみましょう〜
STEP4:最後は線分図から答えを計算しよう!

残すところあとわずかです。がんばりましょう!
STEP3までで、母と子の年令の線分図に情報を書きこむことができました。
あとは計算していくだけです!
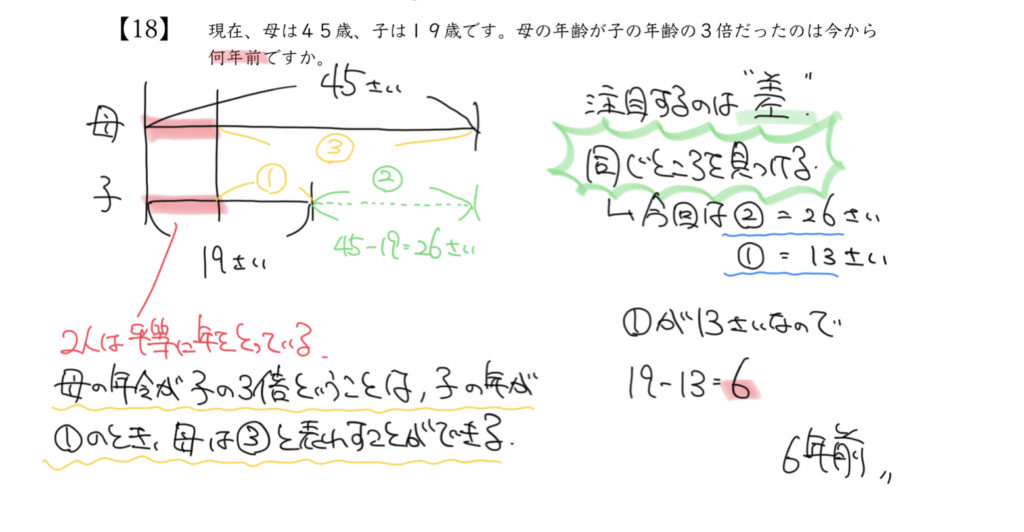
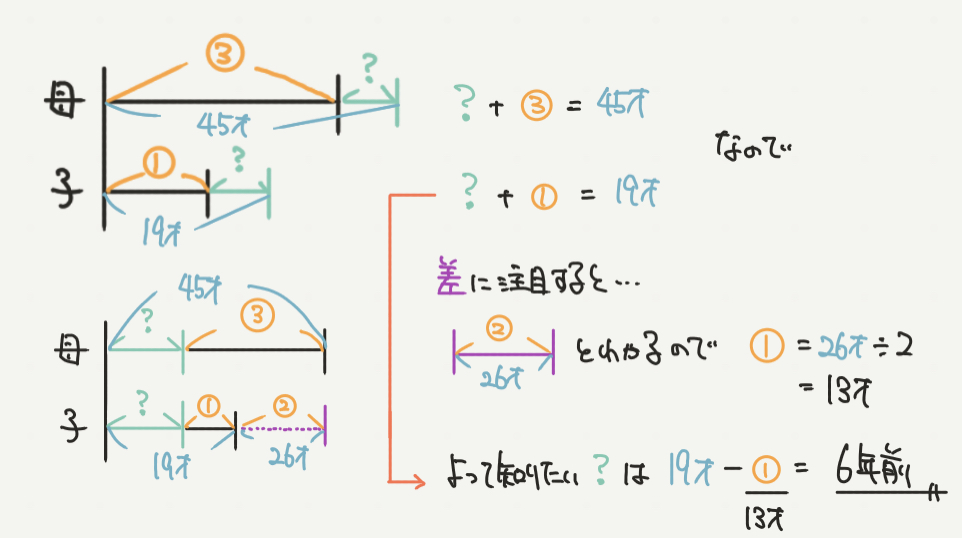
ここで、注目して欲しいのが紫色の部分です。
母親の年令と子の年令の差を見てみてください!
母と子の差は③−①=②、とわかりますよね?
そして年令で計算すると、
母親(45才)−子(19才)=26才とも書けると思います。
つまり、②=26才に対応していることになります!
ここから①=13才と計算できますので、知りたい?の数は
母:③+?=45才
子:①+?=19才
これに①=13才を当てはめると、
?=19才−13才
?=6才
と答えを求めることができました!
親子の年令の比からある年数を求める問題のまとめ
今回の問題で大事なポイント
年令算の考え方(STEP2:増える年令は同じ)
線分図の書き方(STEP1、3:しっかり問題文の内容を図にしよう!)
比の足し算(ふつうの数と比は足してはだめ!)
「年令算」のポイント
今回出てきた「年令算」の問題ですが、いかがでしたか?
算数の問題で基礎となる面積図や線分図さえきちんと書ければ解くことができたと思います。
ただ1点、年令算で大事な考え方がありましたね。
それが増える年令の割合は一緒、ということでしたね。

今回は母親と子供ですが、年令算で出てくる登場人物は平等に年をとります。
なので同じところ(とった年)に注目し、そこから差を見つけます。



差はSTEP4の紫のところですね!
最後に気をつけて欲しいのが、比の足し算です!



こちらの比についてはまた今度詳しく説明しますね!


年令の問題は受験でたまーに出るくらいの問題ですが、
だからこそ、周りの受験生と差が出るポイントでもあります。
きちんと復習しておきましょうね!