【中学受験算数】理科みたいな算数の問題！「割合と比」を線分図を書いて攻略！バネの伸びから元のバネの長さを求めてみよう！

はじめに

みなさんこんばんは！！
今日は算数の問題、というよりは理科に近いバネの問題にチャレンジしていきましょう！
バネは私たちの生活の中でもたくさん見かけますね。

たとえば、シャープペンシルとか、エレベーターとか、車とかにもバネが使われています！！
それではいつも通り、まずはバネの基本について勉強しましょう！

バネの考え方

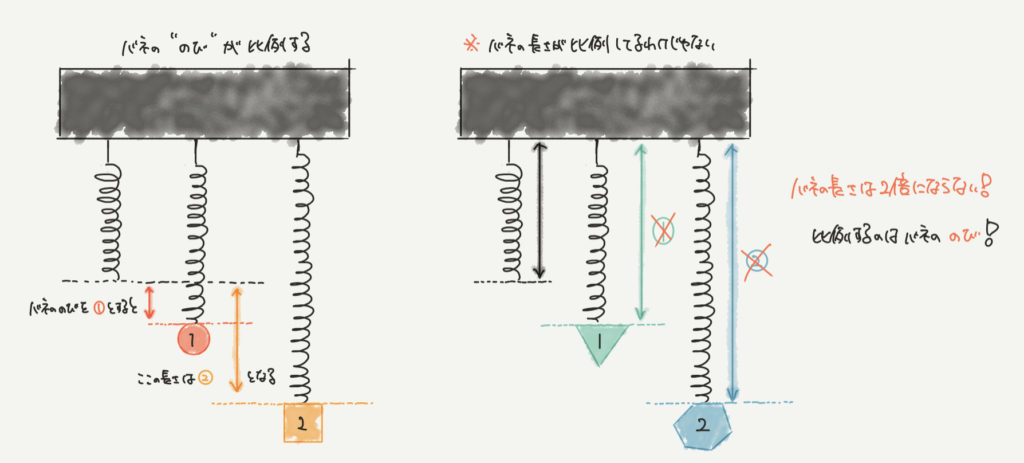
バネの伸のびはおもりの重さに比例ひれいする

受験生のみなさんもバネを使って遊んだことが一度はあると思います。
重いものをぶら下げた方がバネって伸のびますよね？

バネの性質として、おもりの重さに比例ひれいするというものがあります。
なので重さが2倍のおもりをぶら下げたとき、バネの伸のびも2倍になります。

バネの長さは比例ひれいしない！

1点気をつけてほしいのが、バネの長さには比例ひれいしないということです。
上のイラストの右を見てもらえばわかると思いますが、長さは比例ひれいしません。

比例ひれいするのはバネの伸のびなのでそこだけ勘違かんちがいしないようにしましょう！

〈プロ講師のみ〉数学が苦手な生徒のための個別塾「数強塾」

問題に挑戦ちょうせんしよう！

あるつるまきばねに27gのおもりをつるすと、長さが12.3cmになり、9gのおもりをつるすと長さが10.9cmになります。何もしていないときのこのつるまきばねの長さは何cmですか。

解答

この記事を書いている人はこんな人

解説を読んで「 割合と比 」を攻略こうりゃくしよう！

↑解説の図ではバネの長さにおもりの長さが足されていますが、正しくはバネのみの長さです。大変申し訳ありません。下の解説では直してあります。

STEP1：問題文を絵にしよう！

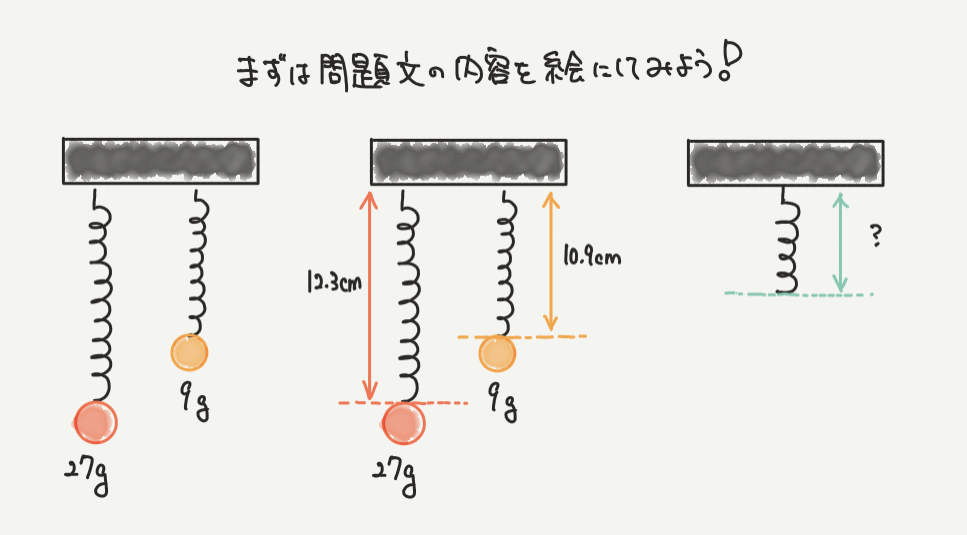
まずは問題文を絵にしましょう。

いつもなら線分図や面積図に直すところですが、今まで解いたことのないような少し変わった問題なのでまずは絵をかいてみました。
むずかしい問題や、ぱっと見て意味不明な問題も、絵にしてみれば理解しやすくなることがあります。

たとえばこの絵では、バネの伸のびと長さ、そして求もとめたいバネの長さを絵にすることができました。
どんな絵をかいても大丈夫だいじょうぶですが、問題文で出てきた情報は必ず全部入れるようにしましょう！

ぜひ問題でこまったら実践じっせんしてみてください！

STEP2：問題文を線分図にしよう！

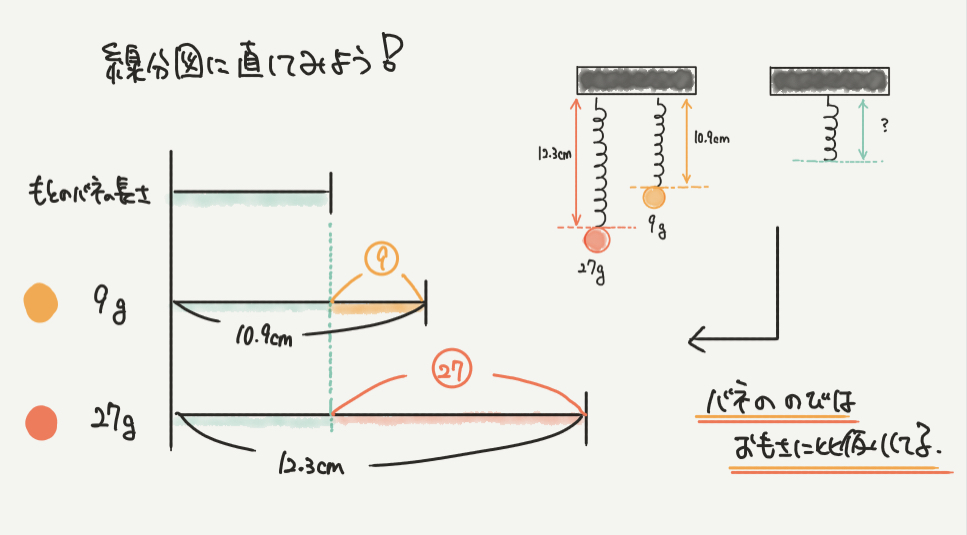
次のステップでは線分図に直してみましょう。

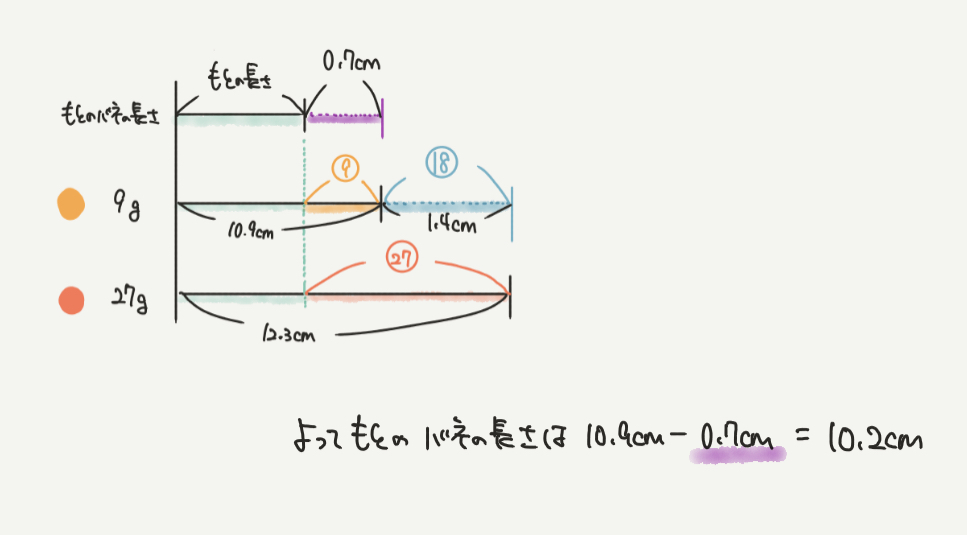
絵の内容をもとに、元のバネの長さを緑、9gのおもりをつけたときの10.9cm、27gのおもりをつけたときの12.3cmを線分図に直します。

ここで気をつけていただきたいのが、どこを⑨、㉗にするのかです。
バネの伸のびと重さが比例ひれいするので、元のバネの長さは関係ありません。

緑の部分以外の黄色、赤色のところがバネの伸のびになります。

STEP3：線分図から差を見つけよう！

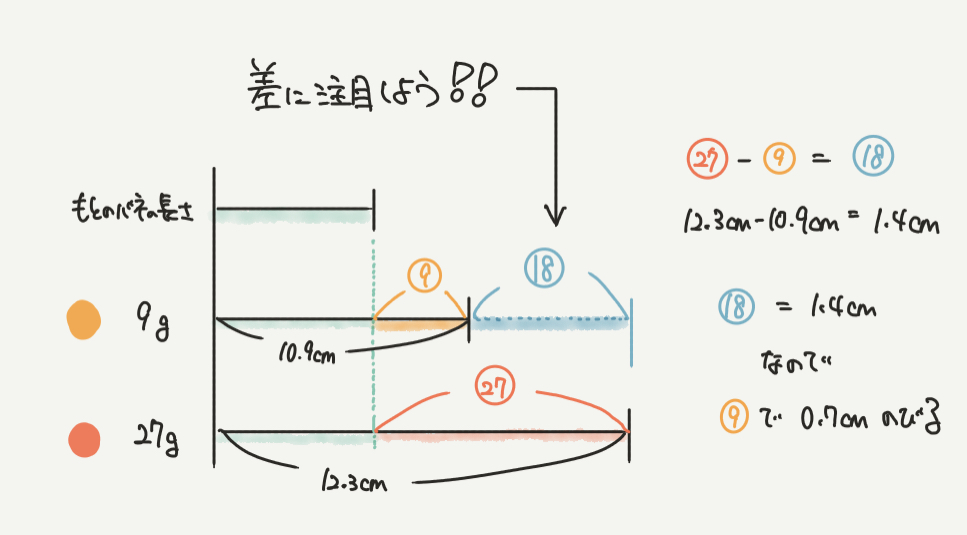
線分図をかいたら、ここから追加でわかることを書きこんでいきましょう。
この図では青色の差の部分に注目すると答えに近づけますよ！

㉗–⑨＝⑱の部分が12.3cm–10.9cm＝1.4cmであることがわかります。
なので、⑱＝1.4cmとなりますね。

最後は計算するだけですが、求もとめたい緑の長さをどうしたら求めることができるのか、考えてみましょう。
求めるために必要な式は、
10.9cm–⑨＝もとのバネの長さ、となりますので、

⑨の長ささえわかれば答えを出すことができます。

STEP4：あとは答えを計算しよう！

⑱＝1.4cmなので、
⑨＝1.4cm÷2で0.7cmと求もとめることができます。

よって答えのバネのもとの長さは、
10.9cm–0.7cm(⑨)＝10.2cm、と計算することができました。

バネの伸びから元の長さを求める問題のまとめ

今回の問題で大事なポイント

バネの考え方（バネの伸のびは重さに比例する）
・バネの長さには比例しない！
・バネの伸びる長さに比例する！
比例についての考え方
線分図の書き方（STEP2、3、4）

今回の問題は算数の問題で出るよりかは、理科の問題に近いかもしれません。
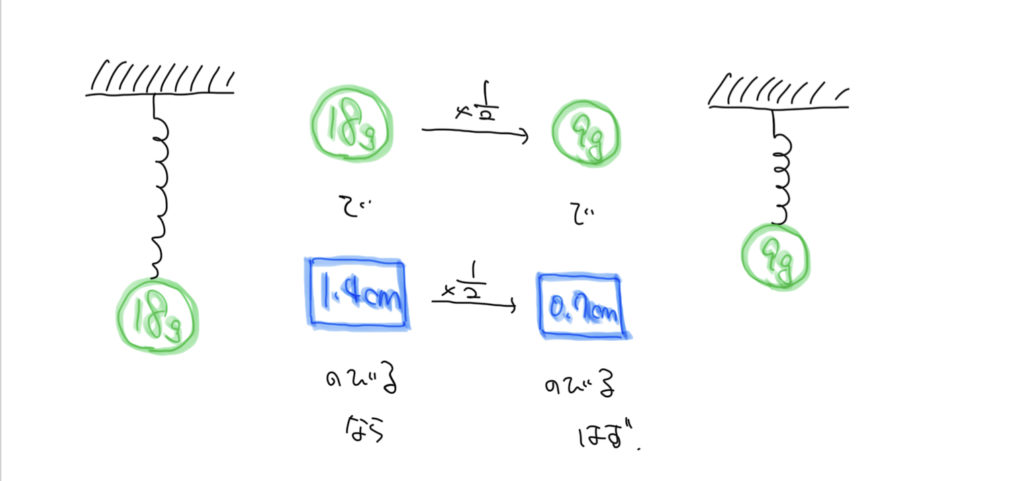
バネの性質として、バネの伸のびの長さとおもりの重さが比例ひれいの関係になっていましたね。

今回18gで1.4cm伸のびるので９gで0.7cm伸のびることがわかりましたね。

ただ忘わすれてほしくないのは、
バネの伸のびが0cmだといってバネの長さが0cmになるわけではありません。

なぜなら元々のバネの長さがあるからです。
比例についての復習もしっかりとして、おさらいしておくようにしましょう！

その他の単元の問題の復習はこちらから！