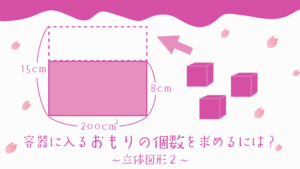
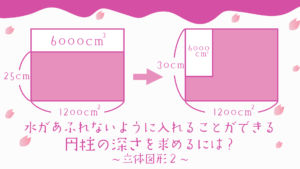
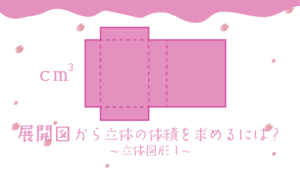
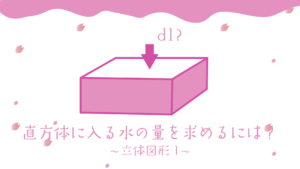
目次
はじめに
みなさんこんばんは!「さんすうがく 」の赤い小人です。
本日も中学受験でよく出てくる「 立体図形 」の問題についてチャレンジしていきましょう。
は〜い!よろしくお願いします!!
今日解く問題は「 立体図形 」の単元ですが、「 割合と比 」で出てくるような食塩水の問題とも考え方は近いです。ですのでまずはその復習からしてみましょう!
「 立体図形」の前に食塩水の復習をしてみよう
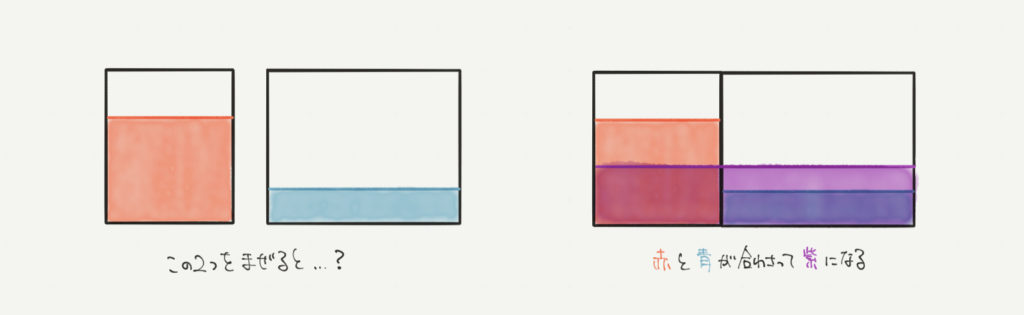
はい!まずは食塩水の復習からです。
食塩水の問題では食塩水をまぜて塩の量を見ていきましたね。
今回の問題では円柱に入っている水の量の移り変わりについておさらいしましょう!
上の図は赤い水と青い水が入っています。
右図ではまぜあわさった水を紫色で表しています。
ここまではOKでしょうか??
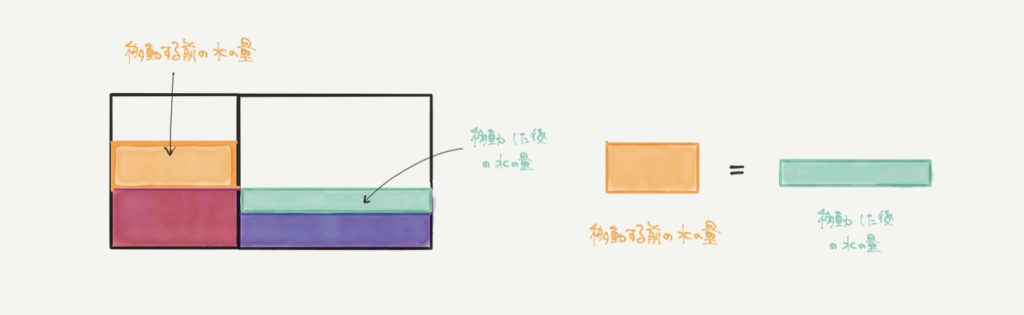
ここでポイントになってくるのが「同じところを見つける、作る」考え方です!
移動する前の水の量と、移動して増えた水の量に注目してください。
移動した部分と増えた部分の水の量は必ず同じになるはずですよね?
なので、移動する前の水の量=移動して増えた水の量と考えることができます。
今回の問題では、この「同じところを見つける、作る」考え方を使って問題を解いていきましょう〜!
「 立体図形 」の問題に挑戦!
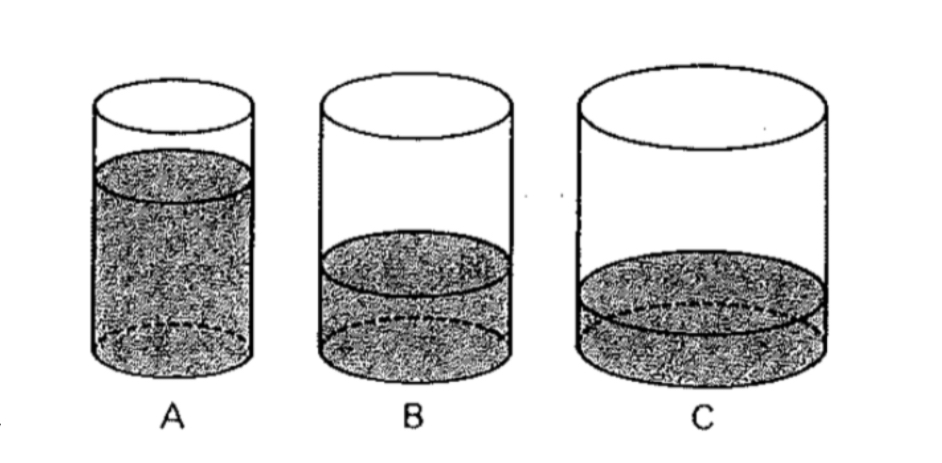
3つの円柱の容器A、B、Cがあります。A、B、Cの底面積の比は2:5:7で、Aには深さ19cm、Bには深さ5cm、Cには深さ3cmまで水が入っています。いま、Aの水の一部をBとCに移して、3つの容器の水の深さを等しくしようと思います。これについて、次の問いに答えなさい。
①等しくなったときの水の深さは何cmですか。
②AからBに、Aの深さの何cm分の水を移すことになりますか。
解答は次のページから!