はじめに
みなさんこんにちは!今日も「立体図形」の問題を解いていきましょう!
今回の「立体図形」の問題では直方体に水を入れるような問題です。
今まで解いてきた「立体図形」の問題と少しちがいますので、
ぜひ自信のある受験生は問題に挑戦!から解いてみてください。
心配な受験生はヒントから一緒に見ていきましょう!
今回知っておきたいポイントは、こちらだけです。
①「立体図形」の問題での面積図の書き方
②水の量の単位
水の量の単位
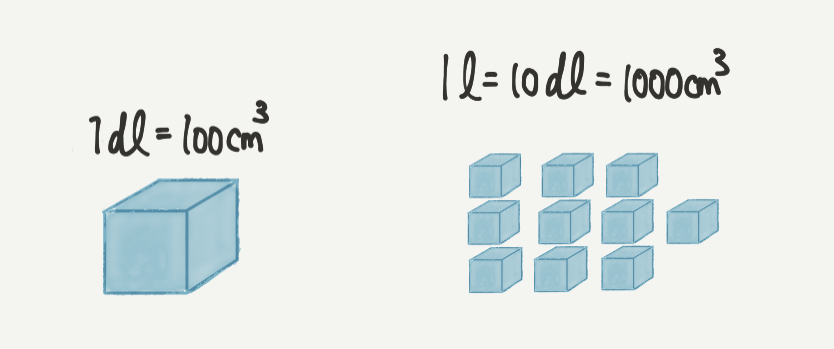
今回の問題では水の量の単位が2つ出てきます。
計算ができても、この単位の計算がわからないと答えを出すことができないので、
ここはしっかりと覚えるようにしてください。
水の量を表す単位は「dl(デシリットル)」や「l(リットル)」などの単位と
「㎤(立方センチメートル)」の単位であらわすことができます。
そして1dl=100㎤となります。
 わかみや先生
わかみや先生この内容さえきちんとおさえておけば、
今回の問題はスムーズに解けるはずです!
さあ!早速チャレンジしていきましょう!!
問題に挑戦!
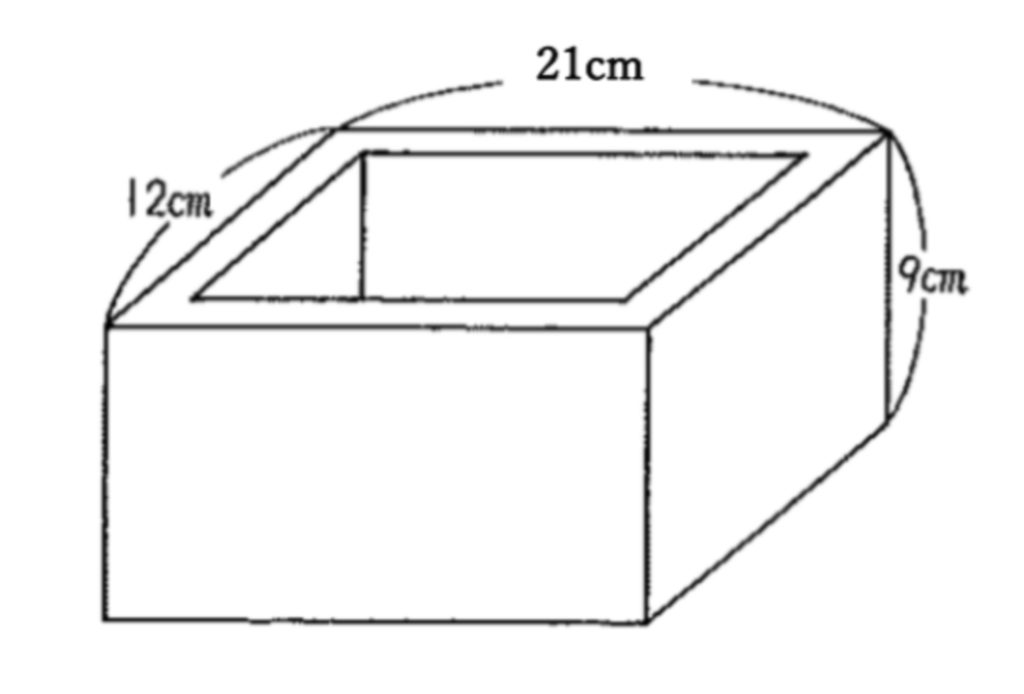

解答
答えを見るにはここをクリック!
①9.52dl
②1316㎤
この記事を書いている人はこんな人




解説を見てみよう!
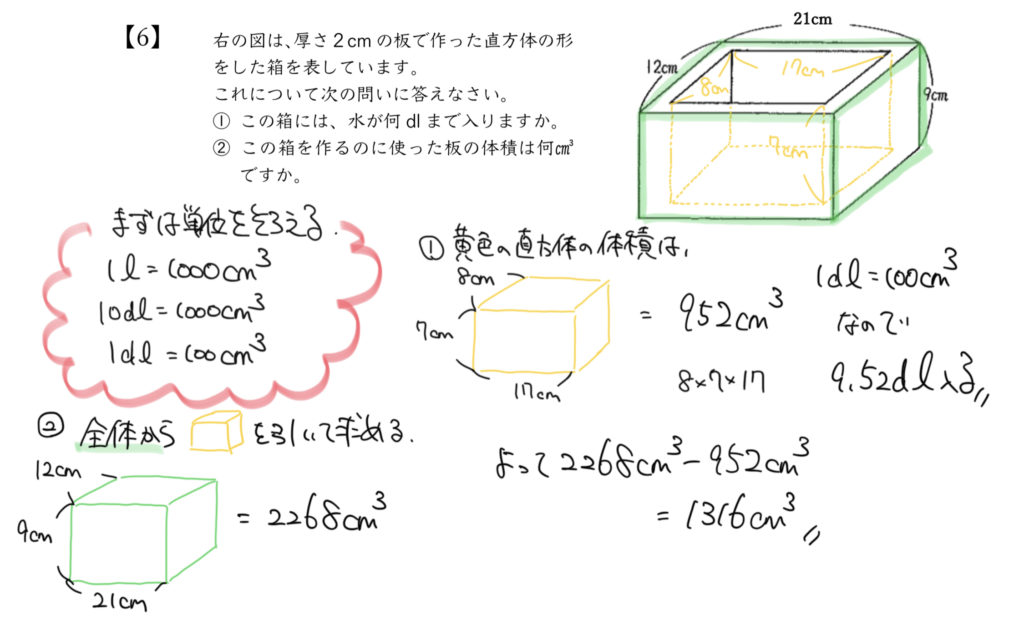

STEP1:補助線を引いて問題文の情報を図に書きこもう
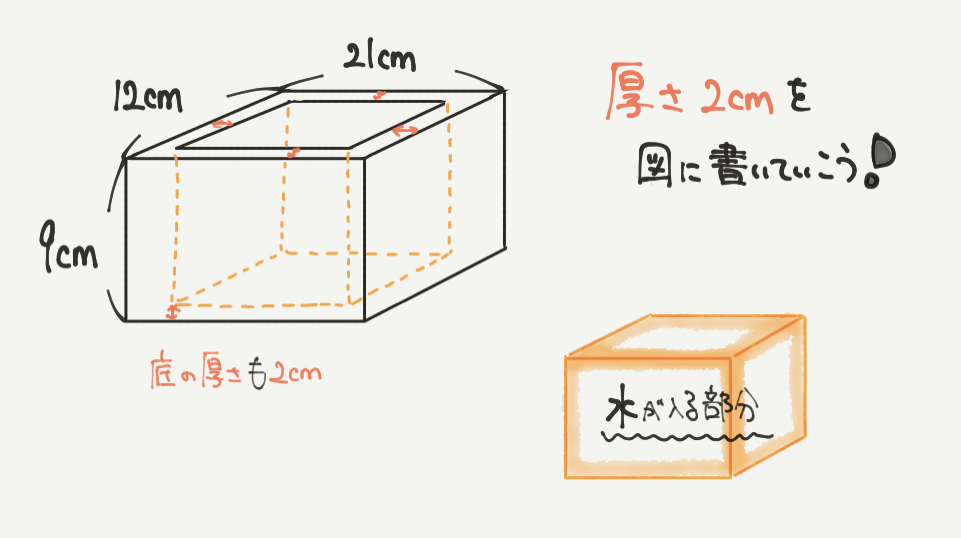

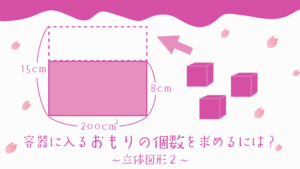
まず今回の立体図形ですが、厚さの2cmがありますので、そのまま計算しないように注意しましょう。
実際に水が入るのは黄色の直方体の部分だけです。
厚さ2cmという情報も小さいですが、図に書きこんでいます。
ここできちんと数字を書いていき、STEP2でケアレスミスをしないようにしましょう。
STEP2:水が入る部分の体積を計算しよう
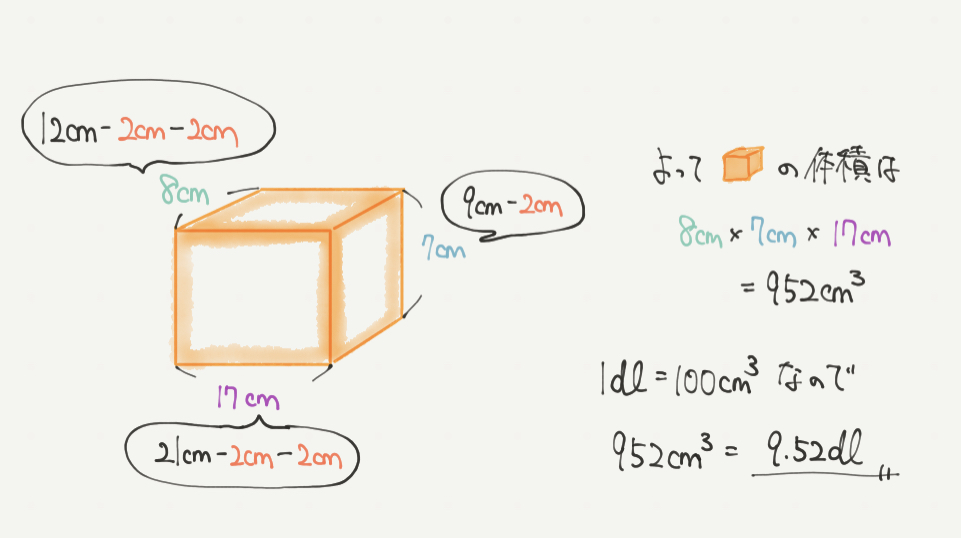

それでは黄色の直方体の体積を求めましょう!
8cm=12cm-2cm–2cm
17cm=21cm–2cm–2cm
↑これらの長さは厚さ2cmを2回引いています。ただし高さの部分だけ気をつけましょう。
7cm=9cm–2cm
高さのところだけ問題の図をしっかりみていると-2cmだけになります。
そしてこれらの長さから黄色の直方体の体積を、
8cm×7cm×17cm=952㎤
1dl=100㎤なので、
952㎤=9.52dlとなります!
STEP3:「全体は部分と部分でできている」考え方を使おう
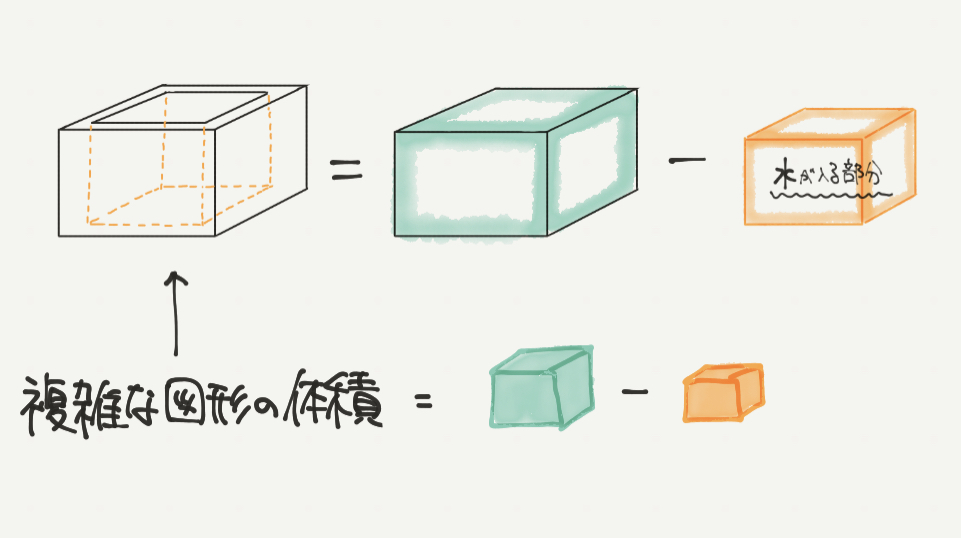

続いてこの立体図形の体積を求めましょう。
こういうときはどうやったら体積をかんたんに求めることができるのかを考えてみましょう。
この立体図スパスパ切って、体積を1つずつ求めても答えは出ます。
でもそれってかなりめんどくさいですし、ケアレスミスをしてしまうかもしれません。
①で求めた952㎤を使えば、実はかんたんに体積を求めることができるんです。
それが全体の緑の直方体から黄色の直方体(952㎤)を引く方法です!
STEP4:それぞれの体積を求めて計算しよう


さあ残りわずかです!がんばりましょう。
緑の直方体は問題文の長さをそのまま使って計算すると、
緑の直方体:21cm×12cm×9cm=2268㎤
黄色の直方体:8cm×7cm×17cm=952㎤
よって体積は引き算していくと・・・
2268㎤-952㎤=1316㎤となりました〜!!
見取り図から直方体に入る水の量を求める問題のまとめ
今回の問題で大事なポイント
- 立体図形で大切な3つの言葉(復習)
・見取り図:いつもよくみる図形、立体的に見える図形のこと
・投影図:真上、正面から見たときに見える図形、平面に見える
・展開図:立体を切って広げたときにできる図形 - 水の量と単位の考え方
・1dl=100㎤



今回もていねいに解説を書きましたが、
むずかしいところはなかったでしょうか?
わからないところがあったら塾の先生に聞いたり、
下のコメントから質問を送ってくださいね!


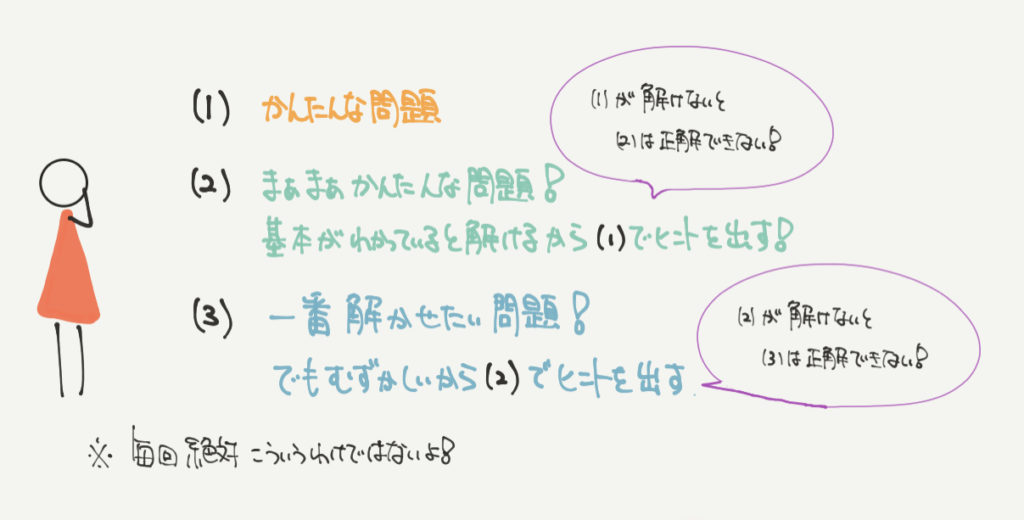
今回のように①、②と連続で問題が出されるとき、実は①を使って②を解く場合が多いです。
偏差値の高い学校ほど問題はむずかしくなりますが、
①は問題を作る人が受験生に出す最初の問題なので簡単なことが多いです。
①を解けば②が解きやすくなる、②が解ければ③が解けるようになっている問題が多いので
問題をつくる側の気持ちに立って解くのもいいでしょう。
たとえば今回の問題では②を解くために①の952㎤を使いましたね?
②を解くためには①のヒントが必要になっていました!
毎回そういうわけではないですが、多くの問題では①や②が次の問題のヒントになっていることが多いです!

「立体図形」の問題は受験生でも苦手な人が多いところです。
きちんと復習するだけでなく、上のように問題をつくる人の気持ちも考えながら解いていくと
周りと差がついていくと思いますよ!!