はじめに
みなさんこんにちは!
「立体図形」の問題もそろそろ慣れてきたころでしょうか?
今日は展開図から立体図形の側面積や対角線の長さを求める練習をしていきましょう。
対角線や展開図はこの前も別の問題でもやりましたね!
忘れてしまった受験生のために、まず対角線についての復習と、
見取り図から展開図へのイメージ図をイラストを使って説明していきます!
さっそくやっていきましょう。
対角線から正方形の面積の求めよう
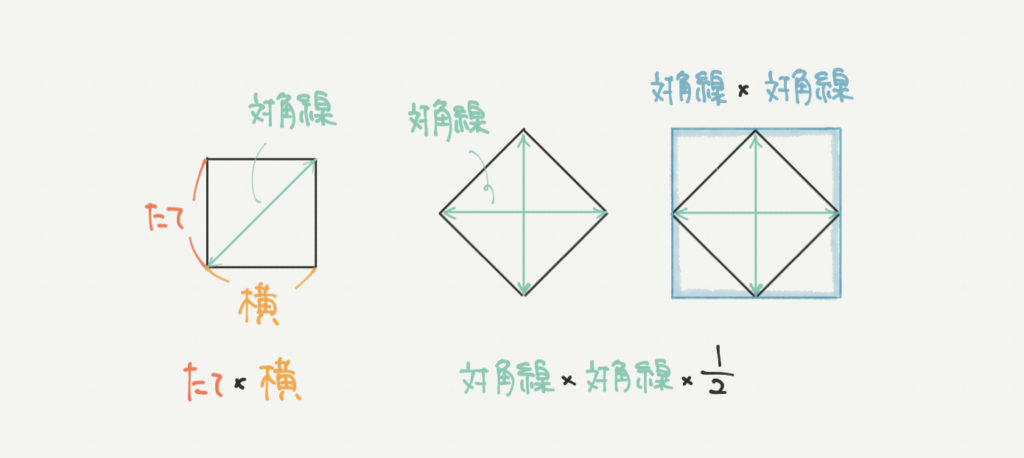
こちらは対角線の長さから正方形の面積を求める式です。
↑「もう知ってるよ!」っていう受験生は読み飛ばしちゃってください!
実は正方形の面積って、「たて×横」のほかにも「対角線×対角線×1/2」でも求めることができるんです!
なぜ「対角線×対角線×1/2」で正方形の面積になるのか?
対角線×対角線をすると青色の大きな正方形ができるのがわかると思います。
対角線が2つとも青い大きな正方形の「たて×横」に当てはまりますね。
求めたいのはこの大きな青い正方形の面積ではなくて、
その中の正方形ですので、×1/2して半分にします。
青い正方形の面積の半分が求めたい正方形の面積ですからね。
正四角すいの展開図を見てみよう
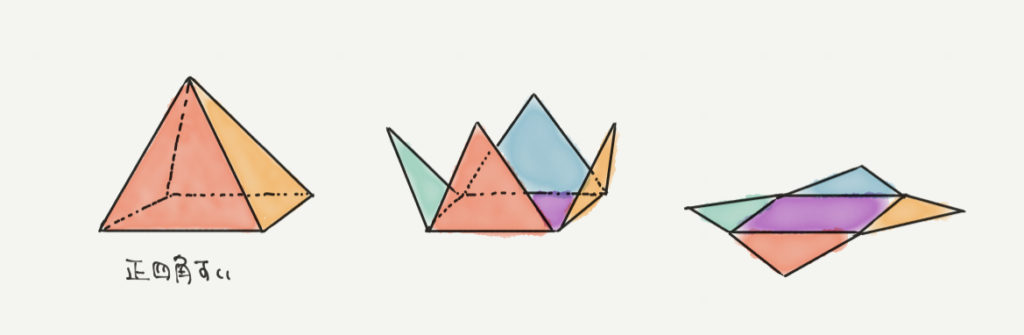
次に正四角すいについて勉強してみましょう。
正四角すいは底面が正方形で周りの三角形が全て二等辺三角形の立体図形です。
上の図のように頭の中でチョキチョキ切って展開していくと、
正方形の周りに赤、黄、緑、青の二等辺三角形が広がるような形になります。
 わかみや先生
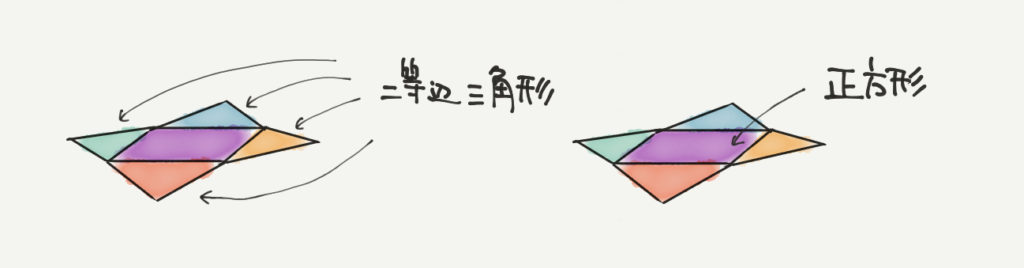
わかみや先生今回の問題ではこれら2つが理解できていないと
解けないようになっています。
まずは上の2つのポイントをおさえて、問題に挑戦していきましょう!
問題に挑戦!
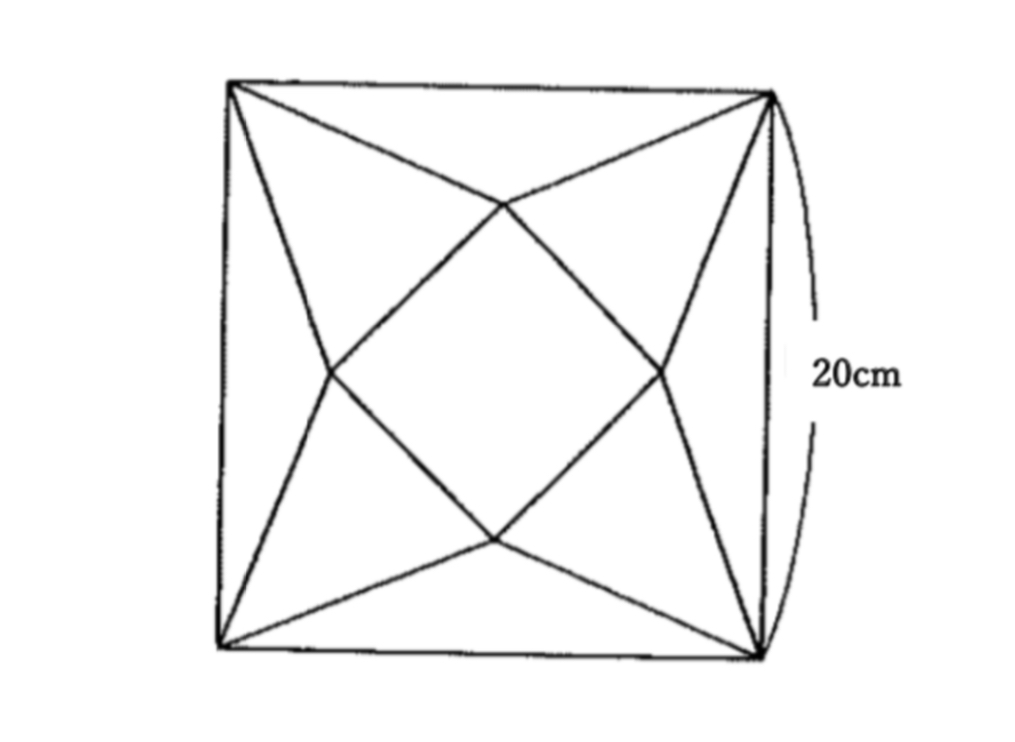

解答
答えを見るにはここをクリック!
①6cm
②25.5㎠
この記事を書いている人はこんな人




解説を見てみよう!
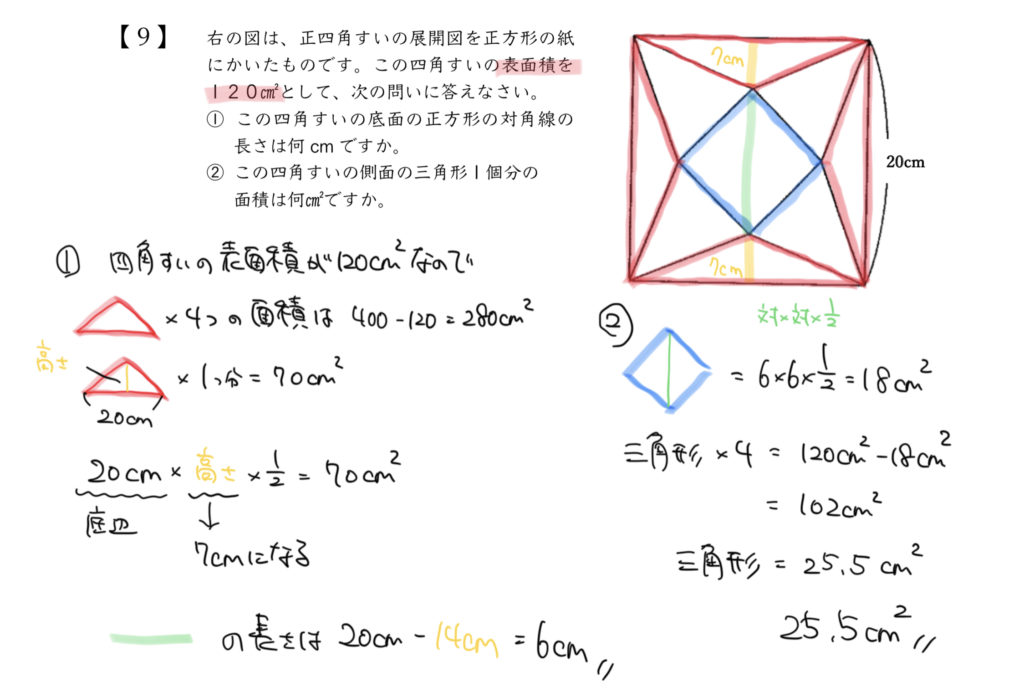

STEP1:問題文の情報を図に書きこみ、同じところを見つけよう
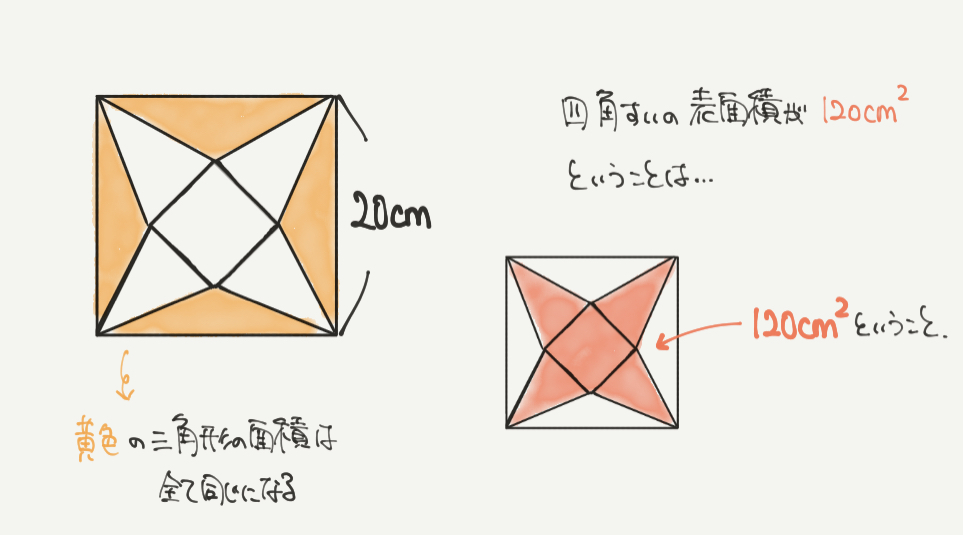

まずは問題文で書かれている120㎠が図のどこの部分に当てはまるのかを考えてみましょう。
さっきご説明したように、正四角すいは正方形と4つの二等辺三角形でできている図形です。
なので120㎠は図の赤い部分になります。
反対に残っている黄色の部分は正四角すいとは関係のない部分の図形になりますね。
この三角形の面積は4つとも同じになります。
これが「同じところを見つける、作る」考え方です。
STEP2:黄色の三角形の高さを求めていこう

正方形の対角線を求めるにはどうしたらいいでしょうか?
実は黄色の三角形の高さを求めていくと、自然と①の答えを出すことができるんです。
STEP1で赤い部分の面積が120㎠とわかりました。
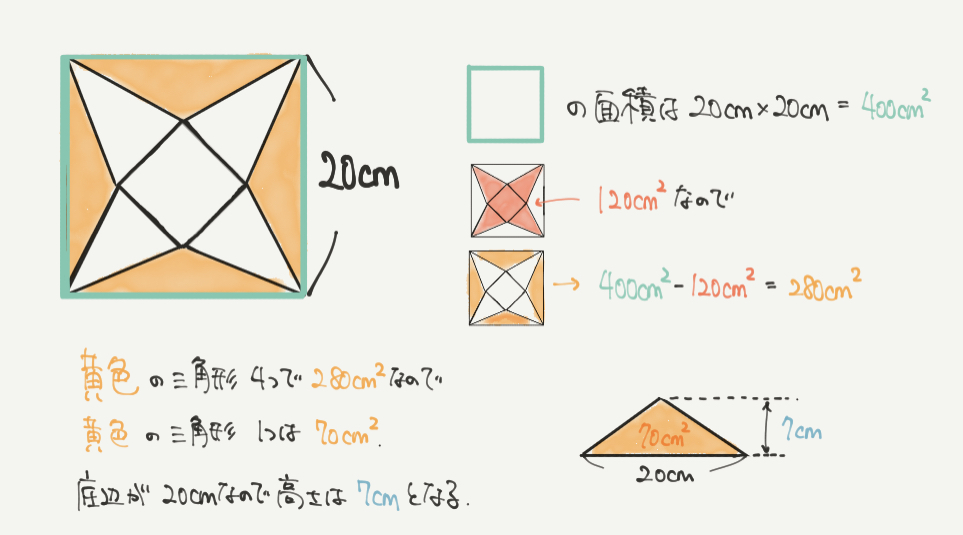
なので残っている黄色の部分の面積は400㎠–120㎠=280㎠となります。
↑20cm×20cm=400㎠(大きな正方形)
よって黄色の三角形1つは280㎠÷4=70㎠となります。
ここから三角形の高さを求めていきましょう。
底辺は問題文から20cmとわかっていますので、
「底辺×高さ×1/2=三角形の面積」というところから
20cm×高さ×1/2=70㎠となり、
高さ=7cmを計算することができました。
STEP3:対角線の長さと正方形の面積を求めよう
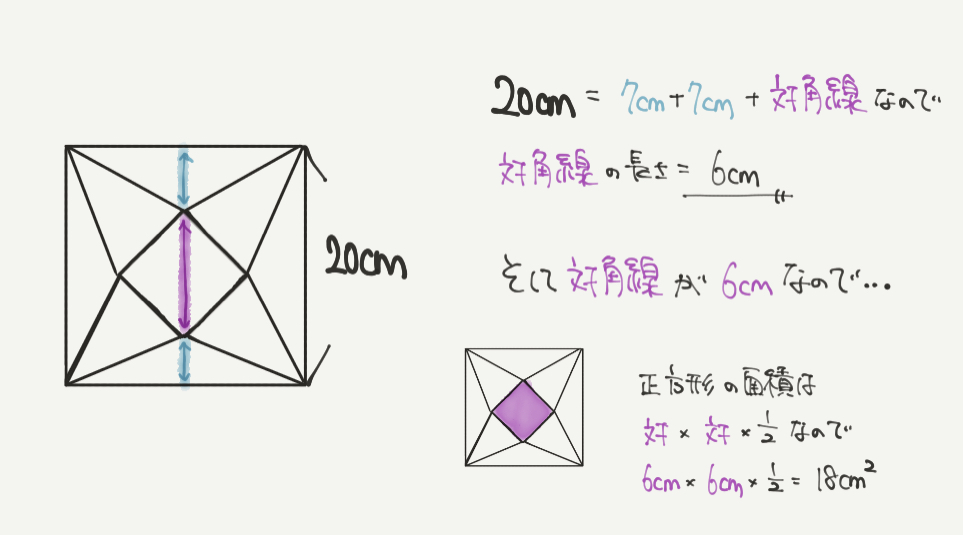

図を見ていただくと、①の答えである対角線の長さは、
正方形のたての長さ(20cm)から高さ(7cm)を2回引いたものだとわかると思います。
ですので、①の答えである対角線の長さは
20cm-7cm–7cm=6cmと求めることができました。
そしてそのまま②の問題について考えていきましょう。
①で対角線が6cmと求めることができたので、紫の正方形の面積も求めることができます。
正方形の面積は「対角線×対角線×1/2」でしたね!!
よってこの紫の正方形の面積は、
6cm×6cm×1/2=18㎠となりました。
さあラストスパートです!!
STEP4:全体を部分と部分に分けて答えを出していこう
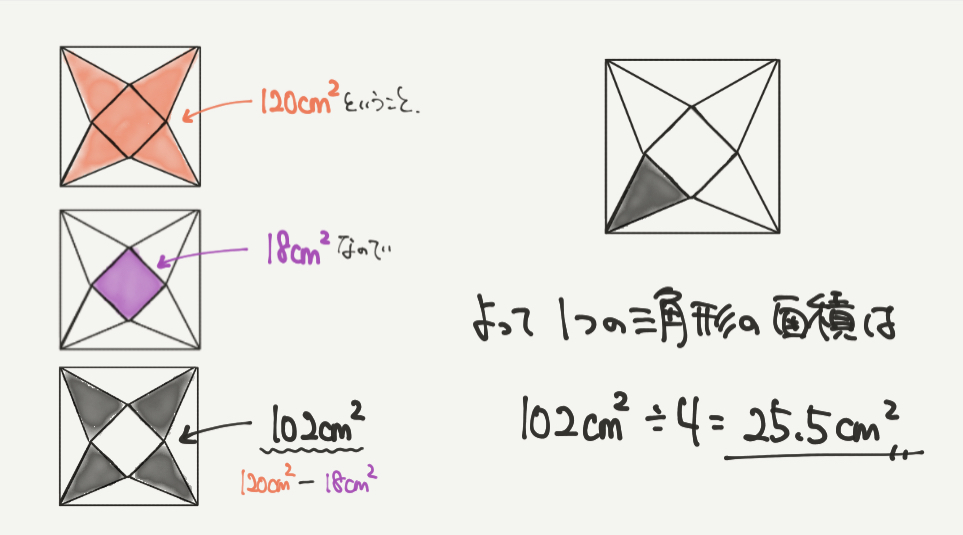

求めたそれぞれの面積を整理すると、
赤:正四角すい全部の表面積が120㎠
紫:正四角すいの正方形の面積は18㎠
なので、
黒:正四角すいの4つの二等辺三角形の面積
の部分が120㎠–18㎠=102㎠になることがわかります。
この②の問題で求めたいのは1つの三角形の面積なので、
102㎠÷4=25.5㎠となります!



全体を部分と部分に分けて考えていきましょう。
今回は正四角すいの展開図の面積(赤)を紫と黒に分けて
考えていくことが大切でしたね!
正四角すいの展開図から長さと面積を求める問題のまとめ
今回の問題で大事なポイント
- 正四角すいの考え方(はじめに、STEP1)
・正方形と4つの二等辺三角形でできている! - 正方形の面積(はじめに、STEP3)
・対角線×対角線×1/2 - 「全体は部分と部分でできている」考え方(STEP4)



大事なポイントが盛りだくさんの問題だったと思います!!
今回の問題は知らないと解けない知識と、
きちんと使いこなさないといけない考え方の2つがありました。
知らないと解けない知識ってなに?
たとえば、正四角すいの展開図は知っていないとわからないですよね?
同じように対角線を使った正方形の面積の求め方も、知らなければ解くことはできません。
このような知っていれば解ける、でも知らないと全くわからない問題は
サクサク復習して頭に入れておくのがいいと思います。
使いこなさないといけない考え方
反対に使いこなさいといけない知識はいつも解説で書いている、
「全体は部分と部分でできている」考え方や「同じところを見つける、作る」考え方のことです。
こっちのポイントは知っていてもなかなか使いこなすことがむずかしいですよね。
私もむかしは、考え方は知っているけど、
どこで使ったらいいのかわからないことがとても多かったです。
解説を見て、問題を解いてをくりかえして、どういうときにどんな考え方を使えばいいのかが
少しずつわかってくると思います。
地道に一歩一歩、問題を解いて特訓していきましょう!!