【中学受験攻略】円すいの展開図問題の解き方とポイント

はじめに

みなさんこんにちは！
今日は「立体図形」の中でも特に苦手な受験生が多い円すいに関する問題です！
全部で5問と盛もりだくさんの内容なので、サクッと解いていきましょう。

今から教えるヒントを勉強してぜひレベルアップしていきましょう！

円すいの展開図

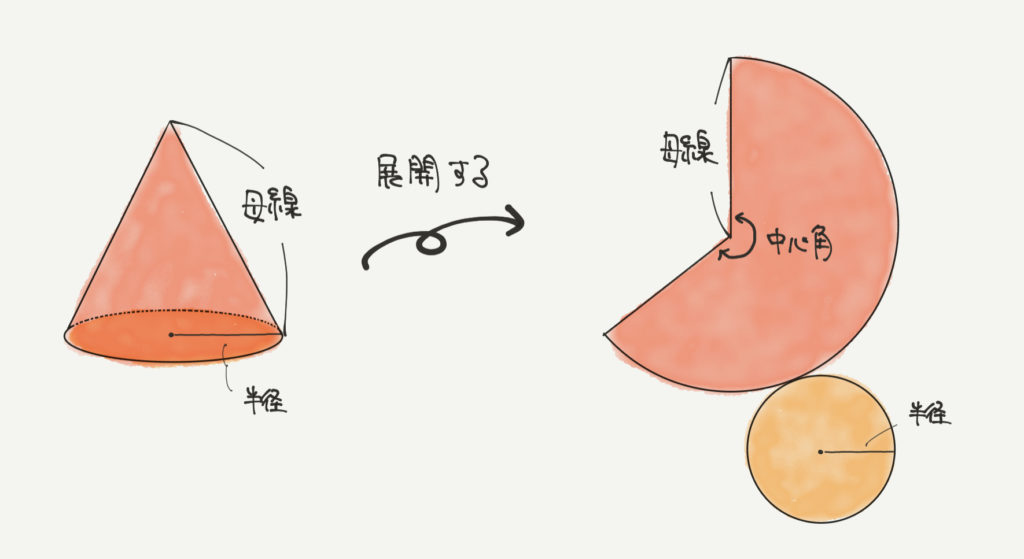
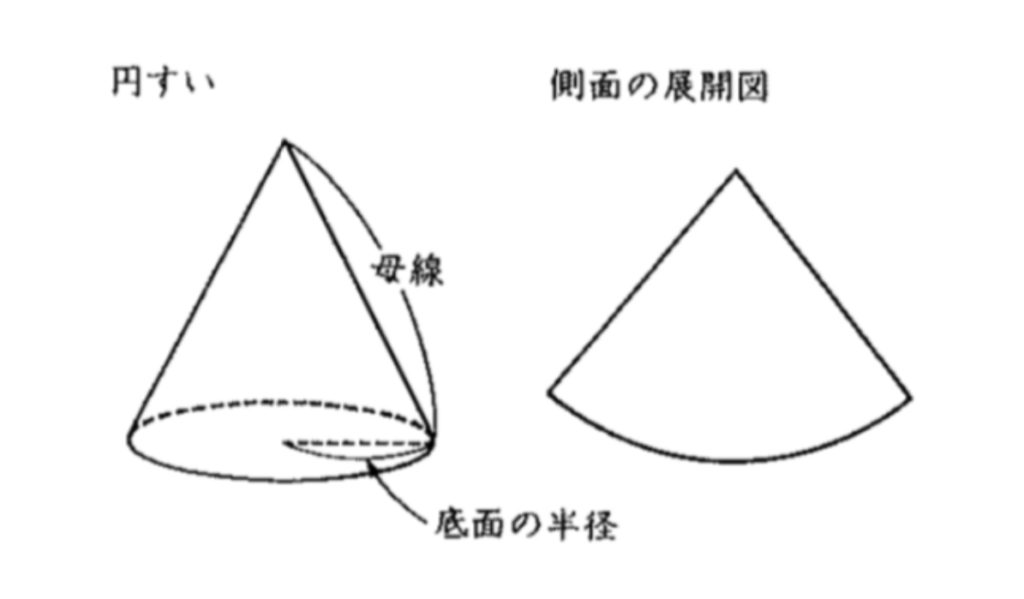
まずは円すいに関する言葉を覚えましょう。
大切なのは「母線」「半径」「中心角」の3つの言葉です。

それぞれが図のどこの部分に当てはまるのかをおさえておきましょう。
そして円すいの展開図は右のようなおうぎ形と小さな円でできています。

このときポイントになるのが、おうぎ形の弧この長さと小さな円の円周の長さが同じだということです。

半径/母線＝中心角/360°

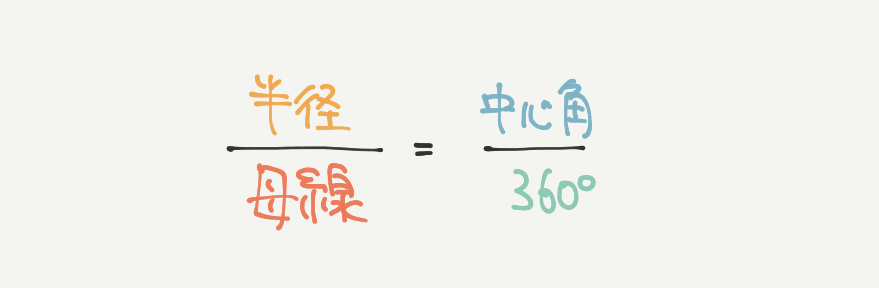
そして今回の問題で一番大事になってくるのがこの「半径/母線＝中心角/360°」という考え方です。

これさえ正しく理解しておけば問題はほとんど解けます！
ただし！！暗記だけしてても良くないので、なんでそうなるのかを確認していきましょう。

さっきの展開図の説明で、おうぎ形の弧この長さと小さな円の円周の長さが同じことについて説明しましたね。
この考え方を使って、本当に「半径/母線＝中心角/360°」になるのかみていきましょう。

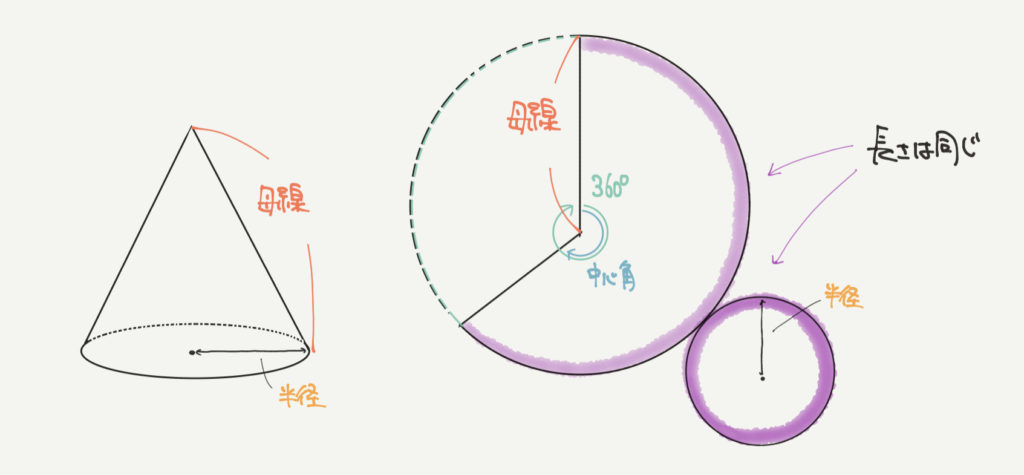
こちらはまず先ほどの図に同じところの長さを書き込んだ図です。
これらの長さが同じなので、それぞれの長さを式で表していきましょう。

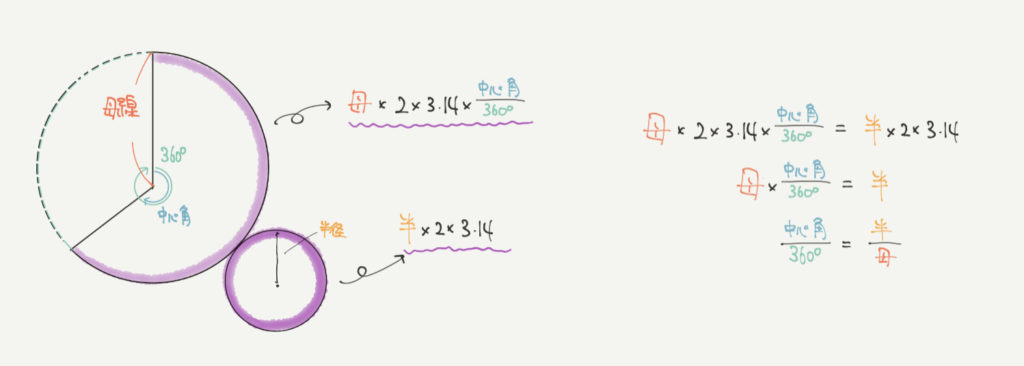
おうぎ形の弧この長さ：母線×2×3.14×中心角/360°
小さい円の円周：半径×2×3.14

この2つの長さが同じなので、
母線×2×3.14×中心角/360°=半径×2×3.14
↑両辺を「2×3.14」で割ると・・・

母線×中心角/360°=半径
↑両辺を「母線」で割ると・・・

半径/母線＝中心角/360°となるわけです！

この考え方さえ理解していれば、たとえば中心角がわからないような問題でも
半径と母線の長さがわかっていれば求めることができます。

このような形でいくつか実践じっせん問題を用意しましたのでさっそくチャレンジしていきましょう。

問題に挑戦ちょうせん！

円すいの側面の展開図はおうぎ形です。円周率を3.14として、次の①〜⑤の問いにそれぞれ答えなさい。

① 円すいの母線の長さが15cmで、底面の半径が5cmのとき、側面を表すおうぎ形の中心角は何度ですか。
② 円すいの母線の長さが24cmで、側面を表すおうぎ形の中心角が120度のとき、底面の半径は何cmですか。
③ 円すいの底面の半径が10cmで、側面を表すおうぎ形の中心角が144度のとき、母線の長さは何cmですか。
④ 母線の長さが24cmで、底面の半径が10cmの円すいの側面積は何㎠ですか。
⑤ 真正面から見ると、正三角形に見える円すいがあります。この円すいの側面と底面積の比を求めなさい。

解答

この記事を書いている人はこんな人

解説を見てみよう！

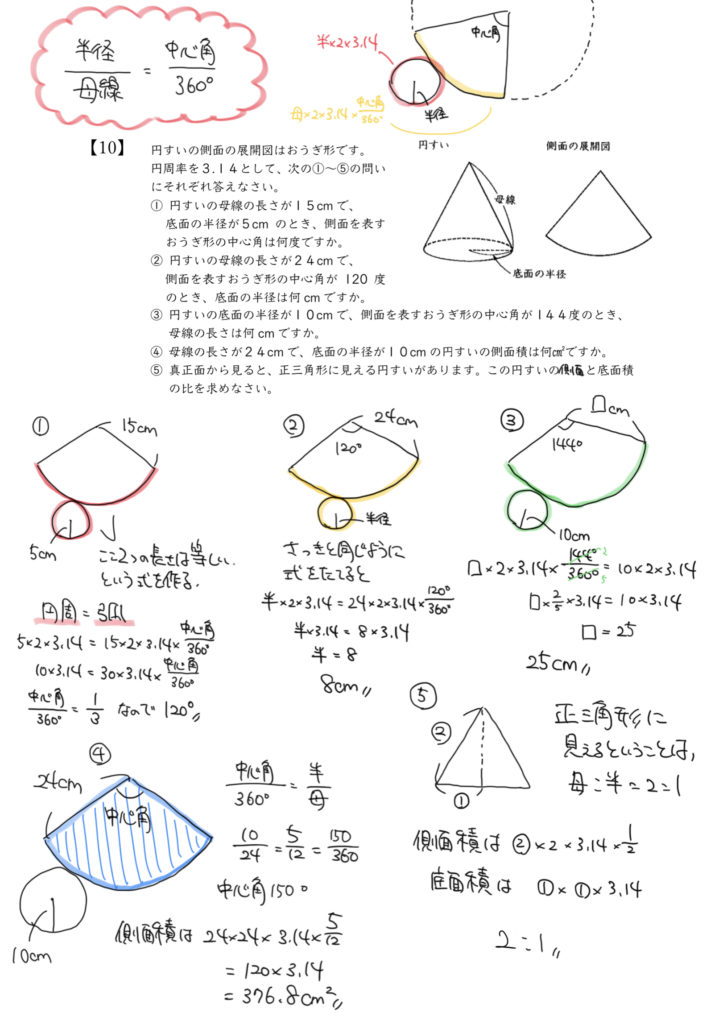
STEP1：円すいの母線と底面の半径から中心角を求めよう

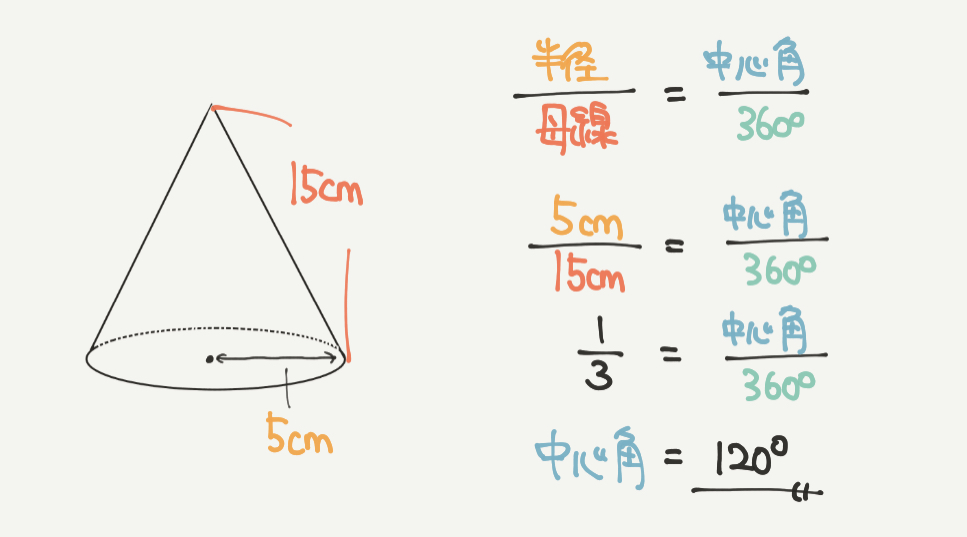
まずは①から解いていきましょう！

といっても、大切なことははじめにで書いた「半径/母線＝中心角/360°」がほぼ全てなので
これに当てはめていくだけです！

半径/母線＝中心角/360°
5cm/15cm＝中心角/360°
1/3＝中心角/360°

なので中心角=120°になります。

STEP2：円すいの母線と中心角から底面の半径を求めよう

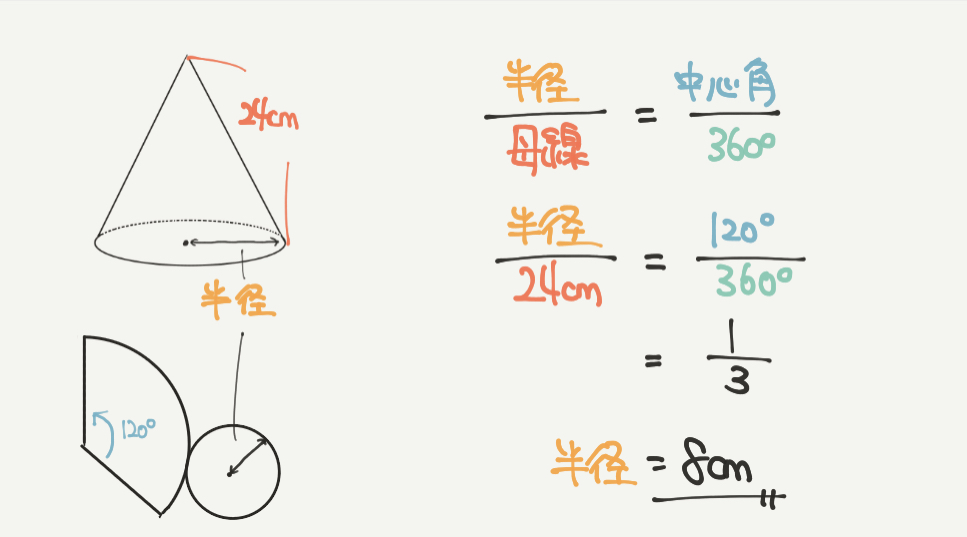
②も同じなのでサクサクいきますよ！

半径/母線＝中心角/360°
半径/24cm＝120°/360°
半径/24cm＝1/3

なので半径=8cmになります。

STEP3：円すいの半径と中心角から母線の長さを求めよう

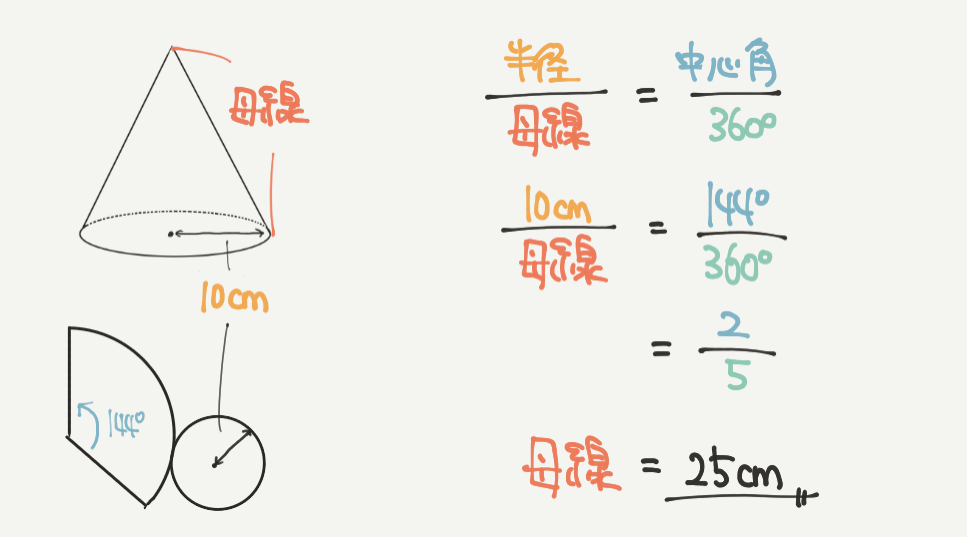
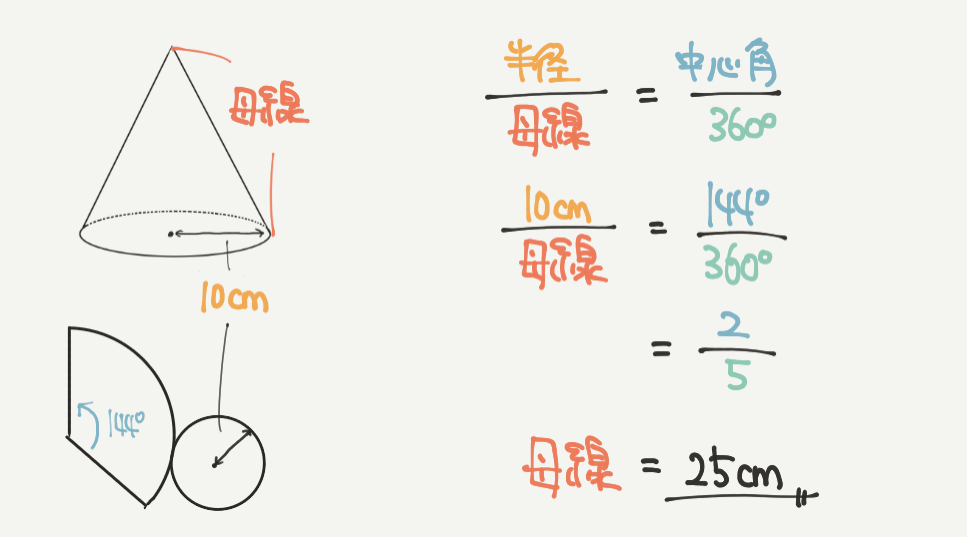
③も同じ！！今度は母線の長さを求めていきます。

半径/母線＝中心角/360°
10cm/母線＝144°/360°
10cm/母線＝2/5

なので母線=25cmになります。

ここまでが「半径/母線＝中心角/360°」の超基本ちょうきほん問題でした。

STEP4から少しレベルアップした問題になっています。

STEP4：円すいの母線と半径から側面積を求めよう

続いての問題では円すいの半径と母線の長さがわかっています。

展開図に直して側面積を計算していきましょう。
側面積は、「母線×母線×3.14×中心角/360°」なので、数字を当てはめていきます。

24cm×24cm×3.14×中心角/360°となります。

ここで「中心角/360°＝半径/母線」を式に代入していきましょう！

すると、
24cm×24cm×3.14×中心角/360°
=24cm×24cm×3.14×半径/母線
=24cm×24cm×3.14×10cm/24cm
=24cm×10cm×3.14
=376.8㎠となります。

STEP5：投影図から円すいの側面積と底面積の比を求めよう

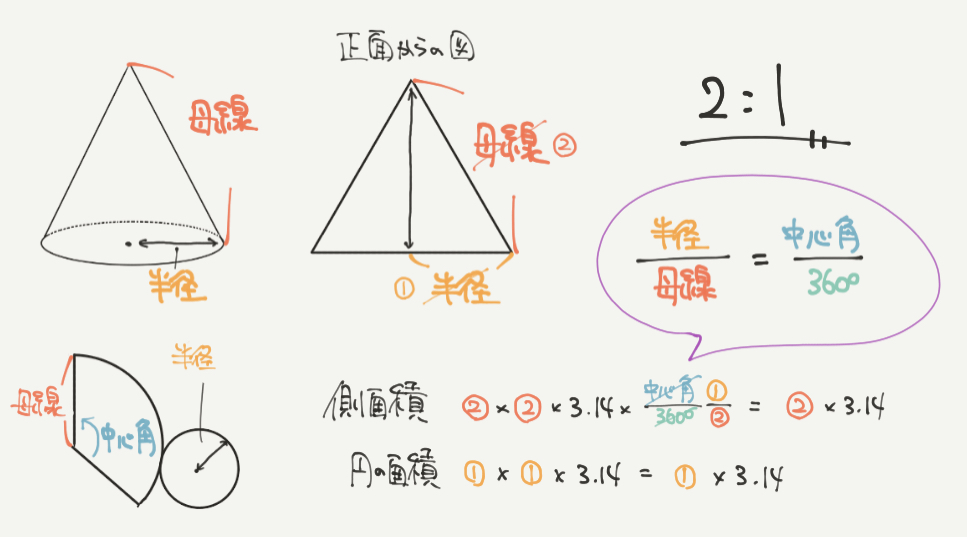
最後は少しむずかしい問題でした。

ポイントになるのが正面から見たときの図（投影図）が正三角形になるということです。
正三角形は全ての辺の長さが等しいので、辺の長さ（母線）とその半分の長さ（半径）の比は2:1になります。

ここから側面積と底面の面積比を計算してみましょう。

側面積：2×2×3.14×中心角/360°
=2×2×3.14×半径/母線
=2×2×3.14×1/2
=2×3.14

底面積：1×1×3.14
=1×3.14

側面積と底面積の面積がそれぞれ計算できましたので、
側面積:底面積=2:1とわかりました！！

おうぎ形の展開図から母線/半径/中心角を求める問題のまとめ

今回の問題で大事なポイント

• 立体図形で大切な3つの言葉（復習）
  ・見取り図：いつもよくみる図形、立体的に見える図形のこと
  ・投影図：真上、正面から見たときに見える図形、平面に見える
  ・展開図：立体を切って広げたときにできる図形
  
• 「同じところを見つける、作る」考え方（はじめに）
• 半径/母線=中心角/360°（STEP1、2、3、4、5）
• 正三角形の考え方（STEP4）

今回何よりも大切だったのは「半径/母線＝中心角/360°」の考え方でしたね。
この内容を正しく理解することが円すいの問題を得意にするコツです。

たとえば、①や②だけ正解しても③を間違まちがえてしまったら
それはきちんと「半径/母線＝中心角/360°」の考え方を理解できていない証拠しょうこです。

「半径/母線＝中心角/360°」の考え方がわかっていれば
①、②、③の3問全部解けるはずですからね！