はじめに
みなさんこんばんは。
夏休みももうそろそろ終わり、少し寒くなってきましたね!
朝と夜で気温の差が大きくなっていますので、体調管理には気をつけるようにしましょう!
今回は「差集め算」とよばれる問題に挑戦していきましょう。
「さんすうがく」ではあまり単元ごとの決まった解説というものはありません。
例えば、「つるかめ算なら絶対に面積図を書け!!」というような解説の仕方は「さんすうがく 」絶対にしません。
なぜなら「さんすうがく」ではさまざまな解き方を使って効率よく問題を解くやり方をすすめているからです。
「さんすうがく 」で解説しているものはあくまでも解説の1つの例です、
なのでこれ以外に正解を出すやり方はたくさんあります。
今回の差集め算は、はじめてやる問題ですが、
今までに教えた線分図や面積図を書くことで簡単に解くことができます。
解説では面積図を使って解いていますが、線分図でも他のやり方でも解くことができます。
ぜひ自分に合った解き方で問題を解いてみる練習をしましょう!
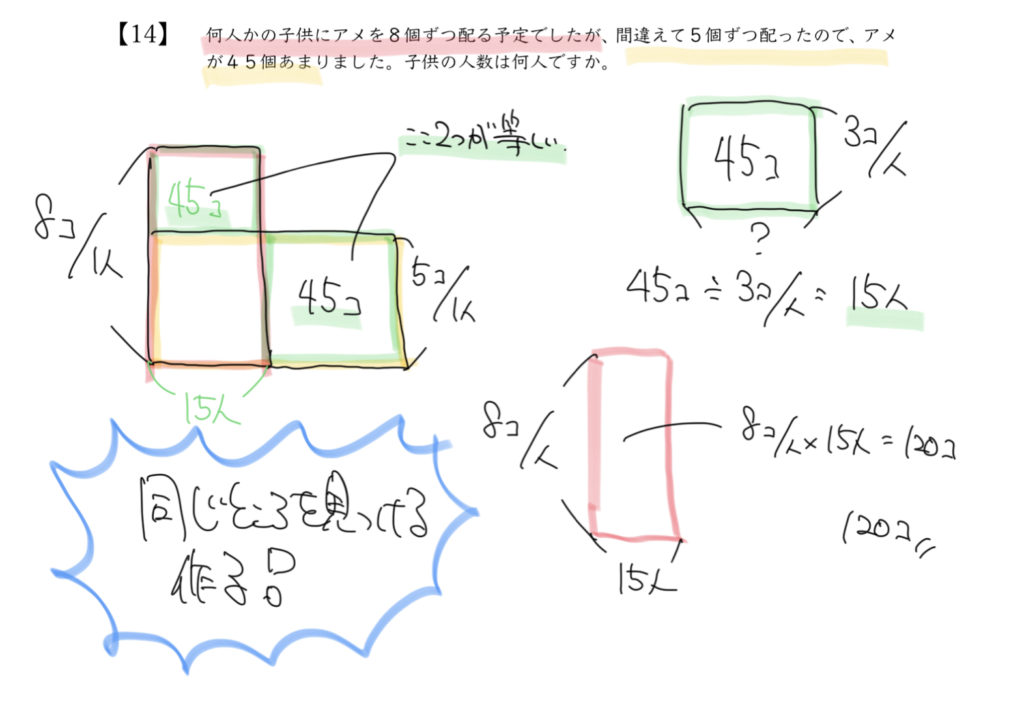
問題に挑戦!
解答
答えを見るにはここをクリック!
15人
手書き解説の方にはまちがえてアメの数(120こ)を書いてしまっていますが正解は15人です。
この記事を書いている人はこんな人

解説を見てみよう!
STEP1:まずは問題文を図にしよう!
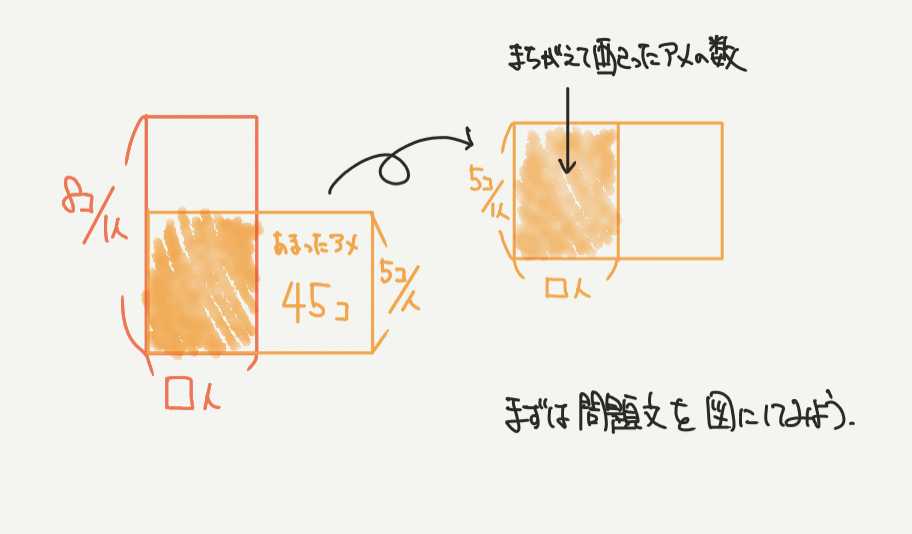
もともと1人につき8個のアメを配る予定だったので赤い長方形のように、
たて(8こ/人)×横(生徒の数が分からないので□人と仮定します)となります。
しかし、実際は1人につき5個のアメを配ってしまったので、45個余ってしまいました。
これを黄色の長方形で表してみましょう。
黄色でぬっているところがまちがえて配ったアメの数になり、
45個の余ったアメを右に書きます。
ここまでがSTEP1です!
まずはわかっていることを図に書いてみましょう。
STEP2:赤い四角形と黄色の四角形は面積同じ!
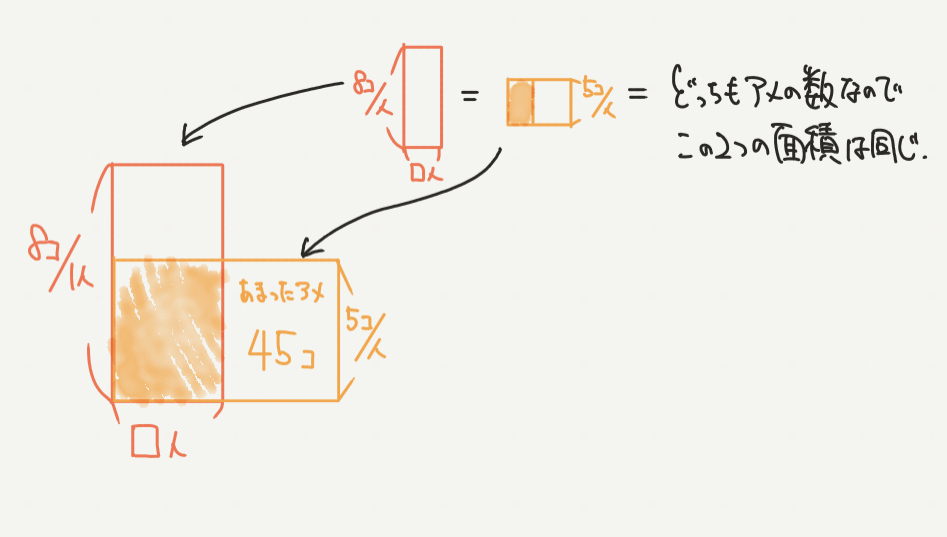
次に注目して欲しいのは赤い四角形と黄色の四角形の面積です。
それぞれの面積は何を表していたのか、おぼえていますか?
はい、どちらもアメの数を表している面積でしたね!
赤い四角形:1人につき8個のアメを配ろうとしていた
黄色の四角形:1人につき5個アメを配ったら45個余った。
どちらの面積も同じときと分かると、STEP3に進みます!
STEP 3:同じところを見つける作る!
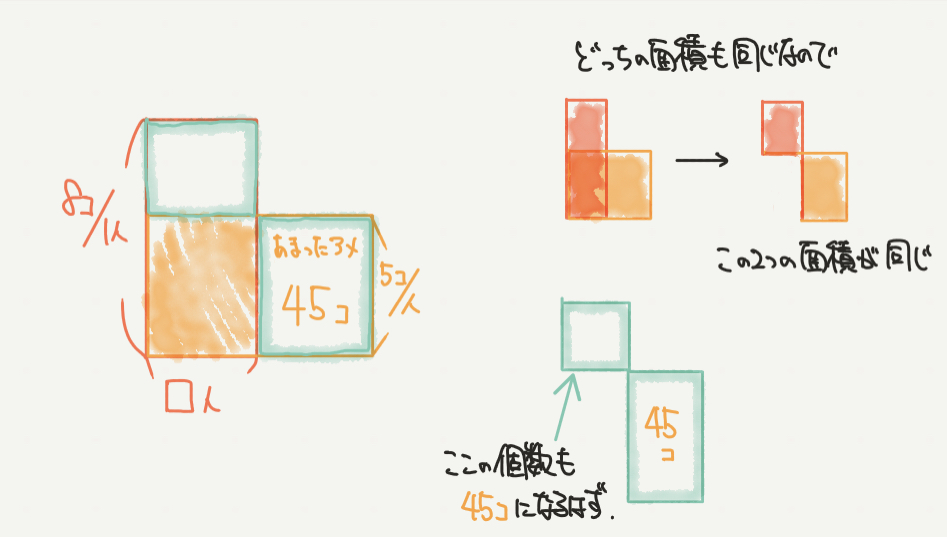
赤と黄色、どちらの長方形の面積も同じ面積だと分かると、
緑の四角形の面積が同じであることがわかると思います。
 わかみや先生
わかみや先生これが分からない人でも大丈夫!下のイラストを見てみてね!
面積図のプチポイント
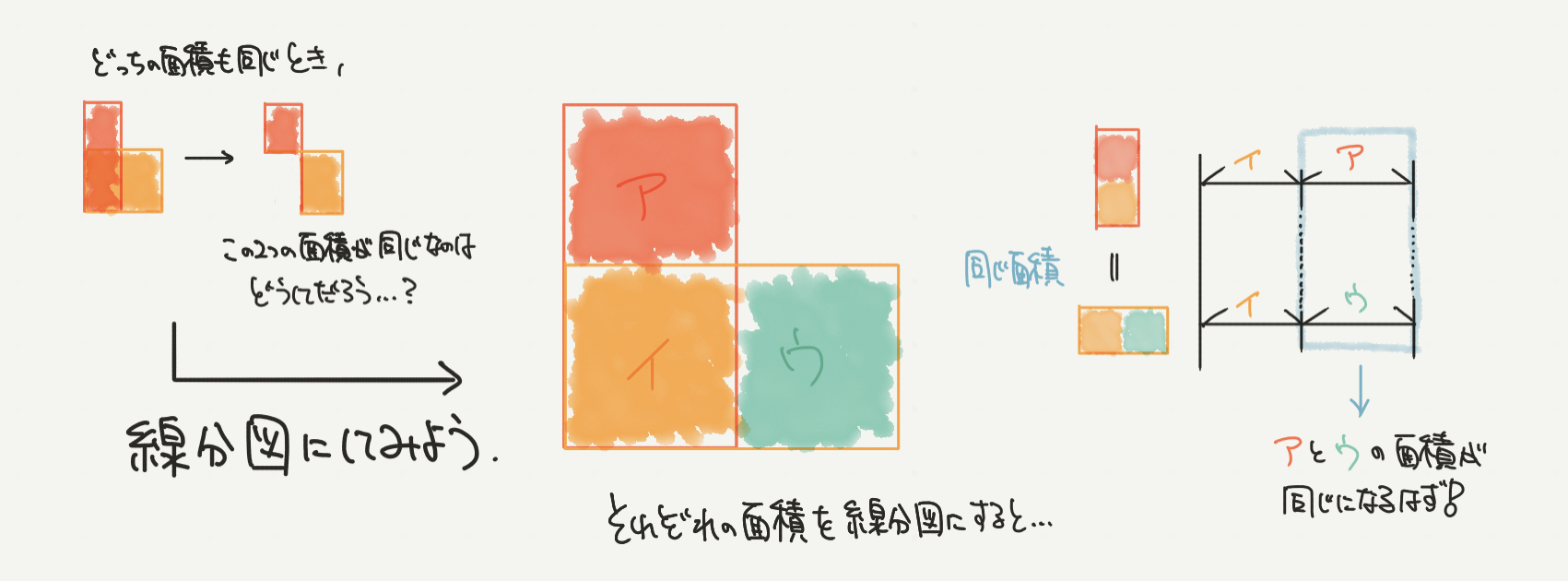

重なった2つの長方形をア、イ、ウを書いてみます。
すると赤い長方形=ア+イ、黄色の長方形=イ+ウとなります。
こちらの2つの長方形を線分図にして表すと、イの部分が同じなのでア=ウと分かると思います!
さて、話をもとにもどします。
この緑の四角形の面積がどちらも同じになりますので、面積は45個と分かると思います。
STEP4:最後はわかるところから計算していく!
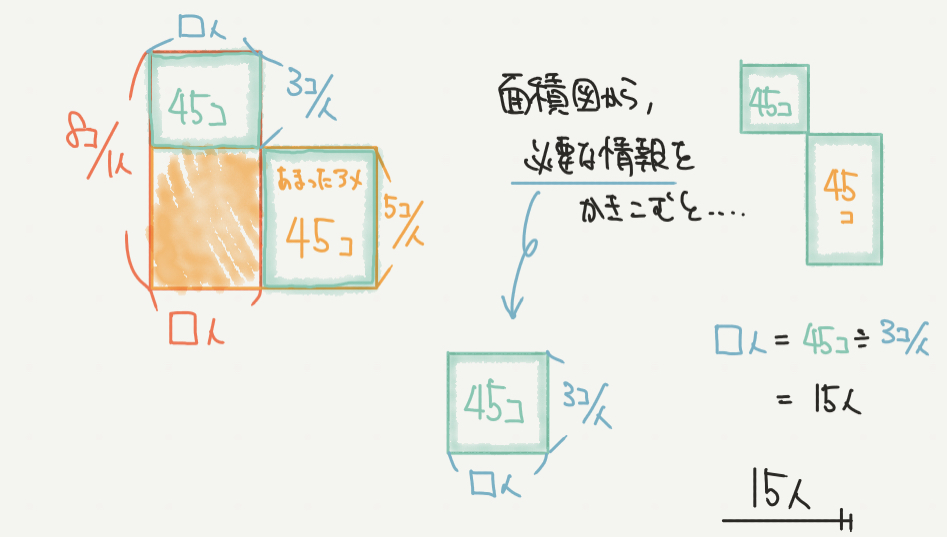

最後に書けるところを青色で書いています!
面積が45個の四角形から□人の数を求めていきましょう。
四角形(45個)=□人(横)×3個/人(たて) となりますので、
人数を45個÷3個/人=15人 と求めることができました。
まちがえて配ったアメの数から子供の人数を求める問題のまとめ
今回の問題で大事なポイント
面積図の書き方(問題文の情報をきちんと図に書こう)
「同じところを見つける、作る」考え方(STEP2、3)
以上で、差集め算の最初の問題はおしまいです。(他にも似た問題はまだまだありますよ!)
いかがでしたか?
今回は面積図を使って解いてみましたが、きちんと勉強することができたでしょうか。
算数の問題を解くコツの一つは、問題文の情報をすべて図に書きこむことです。
反対に、すべての情報をかかなければ問題を解くのはむずかしくなるので、解答例をよく参考にしましょう。
そしてもう一つ大事だったポイントが、同じところを見つける作るという考え方です。
今回も同じだったのは、赤と黄色の四角形の部分です。
これが分かるとSTEP2からSTEP3へ問題を進めることができますし、
ここが見つけられないと解くことができなくなってしまいました。
この同じところを見つける、作るという考えは仮定する考え方と
同じくらい算数では大事な考え方なので、ぜひ覚えておいてくださいね!