はじめに
みなさんこんにちは!今日のテーマも「立体図形」についてです。
「見取り図」「投影図」「展開図」の3つの言葉を今回も使っていきますよ!
見取り図:いつもよくみる図形!
投影図:図形を真上や真横から見たときの図形!
展開図:立体を切って広げたときでできる図形!
ですね!
これらの言葉の復習は前回しましたので、今回はヒントは少なめで問題にチャレンジしましょう。
見取り図を展開図に変形しよう!
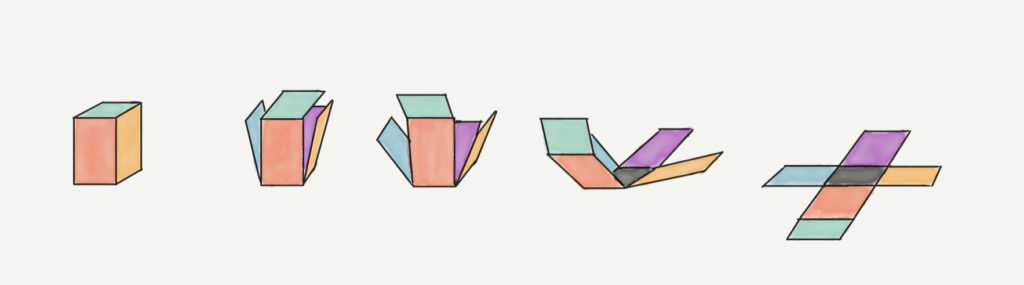
立体図形は自分で紙を使って折り曲げながら勉強してみるのがおすすめです。
上の図は直方体を展開図に変形しているときの様子です。
私の頭の中ではこんな感じで立体を変形しています。
対応する色を見ながら、頭の中でイメージできるようにしてください!
今日の問題はシンプルなので、サクッといきましょう!!
問題に挑戦!
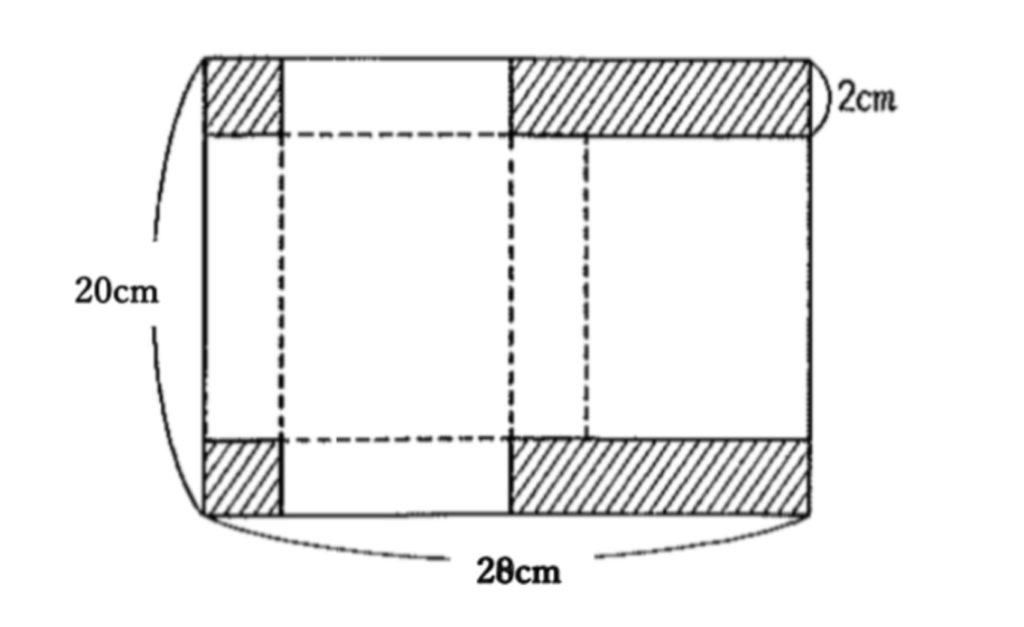
解答
答えを見るにはここをクリック!
384㎤
この記事を書いている人はこんな人


解説を見てみよう!
STEP1:問題文の内容を図にしよう
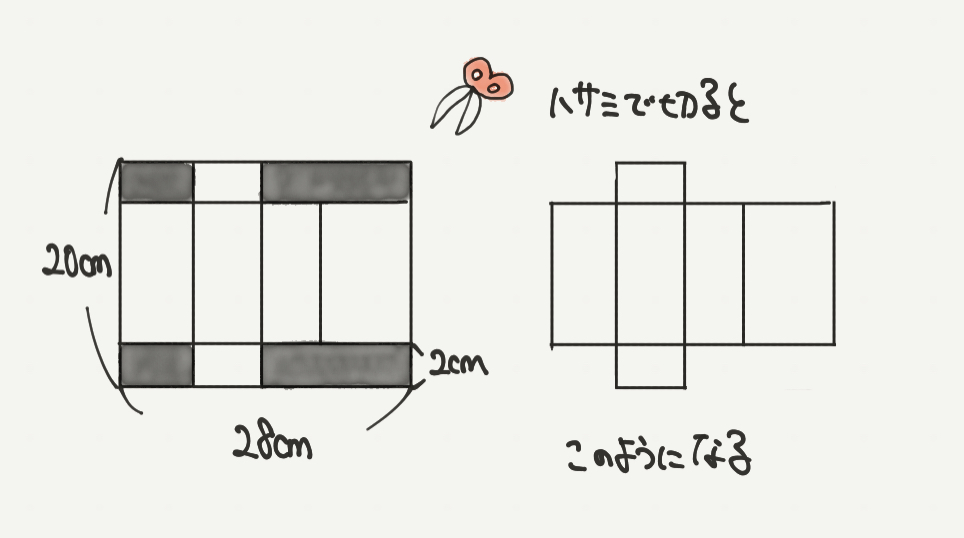
まずは問題文の内容を図にしていきます。
とは言っても今回は展開図が書かれていますので、そのままこの図を使ってしまいましょう。
黒でぬったところは切り取ると問題文に書いてあるので、
ハサミで切り取ると右図のようになりますね!
ここまでがSTEP1です。
STEP2:同じところを見つける考え方
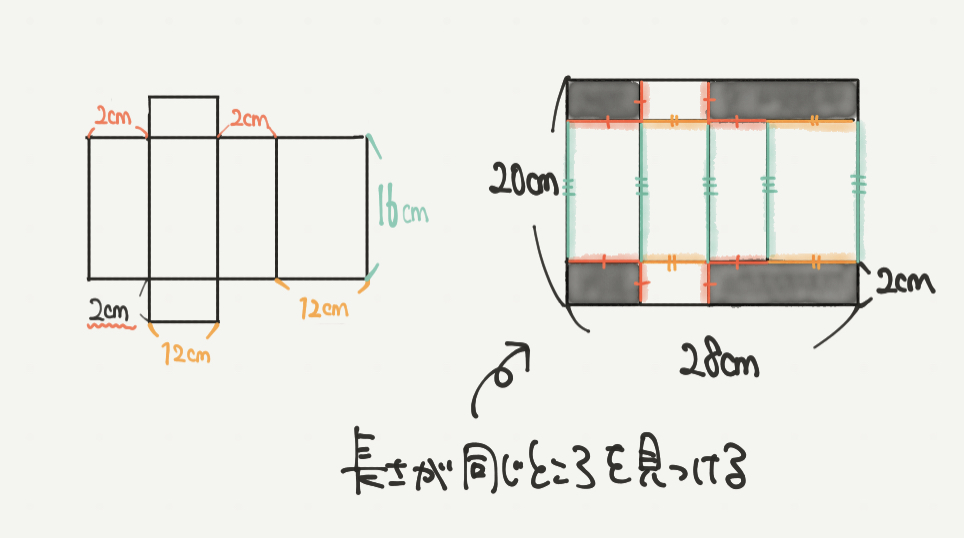
図形を切り取って展開図にしたら、同じ辺の長さの部分に注目していきましょう。
この図形は展開図と言われていましたが、逆に言えば展開図なので、
この図形は必ず組み立てることができるということになります。
図形を組み立てることができるので長さが同じ部分があります。
それがこの図の赤、黄、緑の部分です。
それぞれの長さを以下のように求めていきましょう!
赤:2cm(問題文で書かれていますね)
黄:12cm(横の長さの合計が28cmなので、?+?+2cm+2cm=28cmから計算しましょう!)
緑:16cm(たての長さ20cmなので、20cm-2cm–2cmで計算できます。)
STEP3:展開図を見取り図になおそう
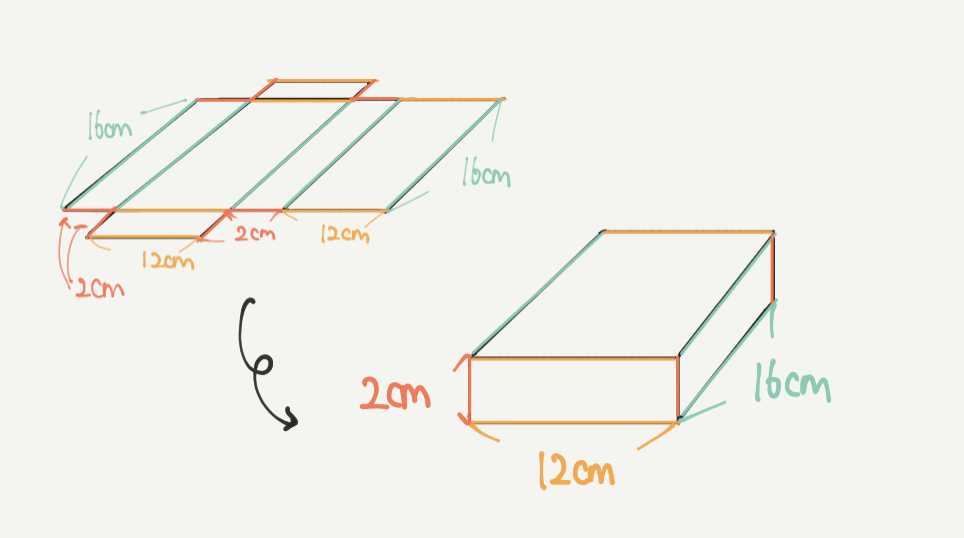
さて、展開図に長さもかけたところでこれらを見取り図に直していきます。
はじめにで勉強したことを活かして、立方体を作っていきましょう。
それぞれの長さを赤、黄、緑の部分で対応させていますので確認してみてください!
STEP4:見取り図から体積を求めよう
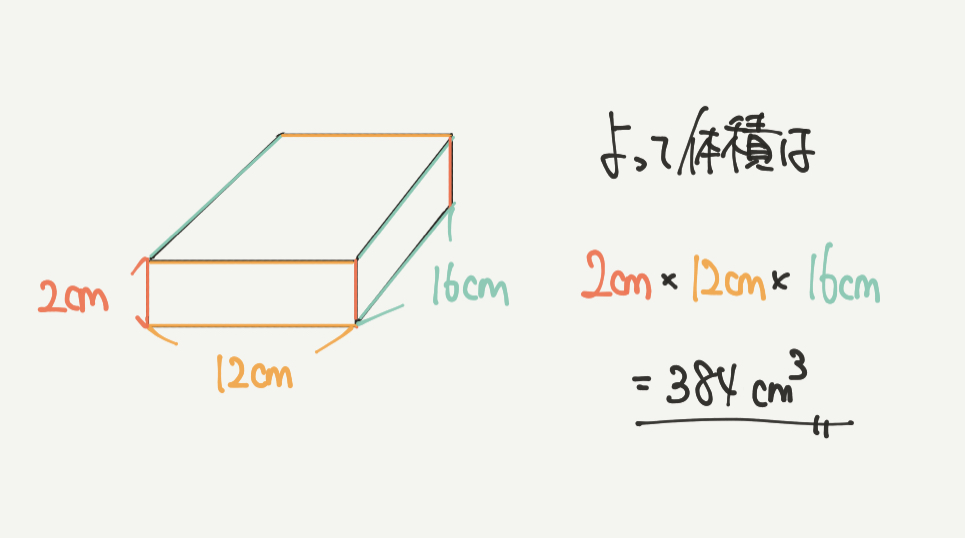
最後は体積を求めていきましょう。
正直STEP4まで考えなくてもささっと解けるような問題かもしれませんが念のため!!
STEP3で展開図を立体図に変形できましたので、あとは体積を求めるだけです。
体積は、
2cm×12cm×16cm=384㎤となりました!
展開図から図形を組み立てて立体の体積を求める問題のまとめ
今回の問題で大事なポイント
- 立体図形で大切な3つの言葉(はじめに)
・見取り図:いつもよくみる図形、立体的に見える図形のこと
・投影図:真上、正面から見たときに見える図形、平面に見える
・展開図:立体を切って広げたときにできる図形 - 見取り図から展開図への考え方(面がどことつながるのか考えよう!)
・「同じところを見つける、作る」考え方
今回の「立体図形」の基本問題はここまでです!
立体図形ではいつも以上にていねいに解説を書いていますが、理解することができたでしょうか?
むずかしいところはなかったでしょうか?
今回の問題は知らないと解けない問題ではなく、今までのおさらいのような問題でしたね!
 わかみや先生
わかみや先生上の2つのまとめポイントの復習問題を下に用意しましたので、
お時間があるときにぜひ解いておいてください!!
見取り図、展開図の復習
6つの展開図から立方体の展開図を求めるには?


同じところを見つける、作る問題の復習
商品の個数と金額の差から買った商品の個数を求めるには?