はじめに
みなさんこんにちは!
「立体図形」の問題もたくさん解いてきましたが、今日はどんな問題でしょうか?
今日の問題は三角柱に水を入れて、その水の量から容器の長さを求めるような問題です。
大切なポイントはいくつかありますが、まずは問題を解くために必要なヒントから見ていきましょう!
角柱の体積の求め方
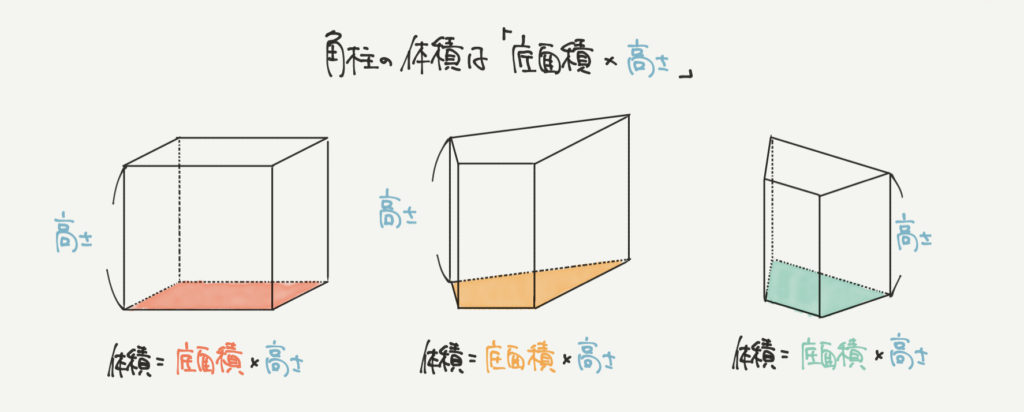
まずは基本のおさらいからしていきましょう。
角柱は「切り口が四角の形をした柱」のことです。
この角柱の体積は「底面積×高さ」で求めることができます。
それぞれの角柱も体積は「底面積×高さ」「底面積×高さ」「底面積×高さ」で計算できます!!
今回解く問題ではこの角柱の体積を使っていきますので、求め方をおさらいしておきました。
さあ!それでは問題を見ていきましょう〜!!
問題に挑戦!
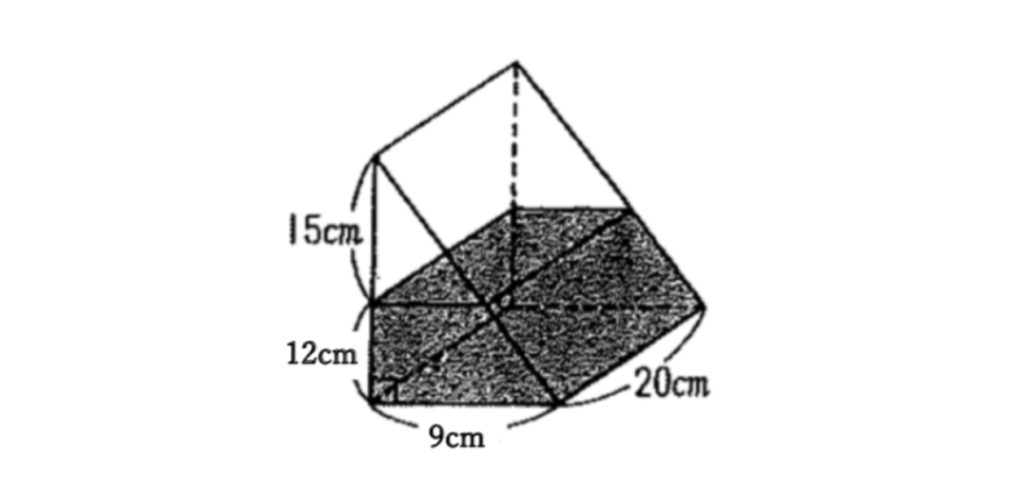
解答
答えを見るにはここをクリック!
1120/81cm
この記事を書いている人はこんな人

解説を見てみよう!
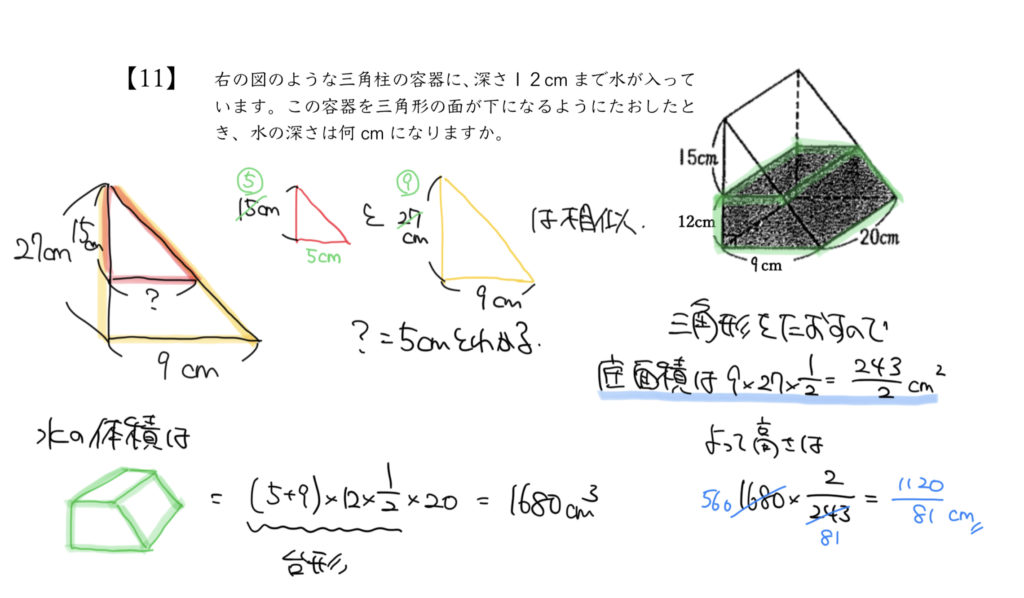
STEP1:問題文の内容を正しく理解しておこう!
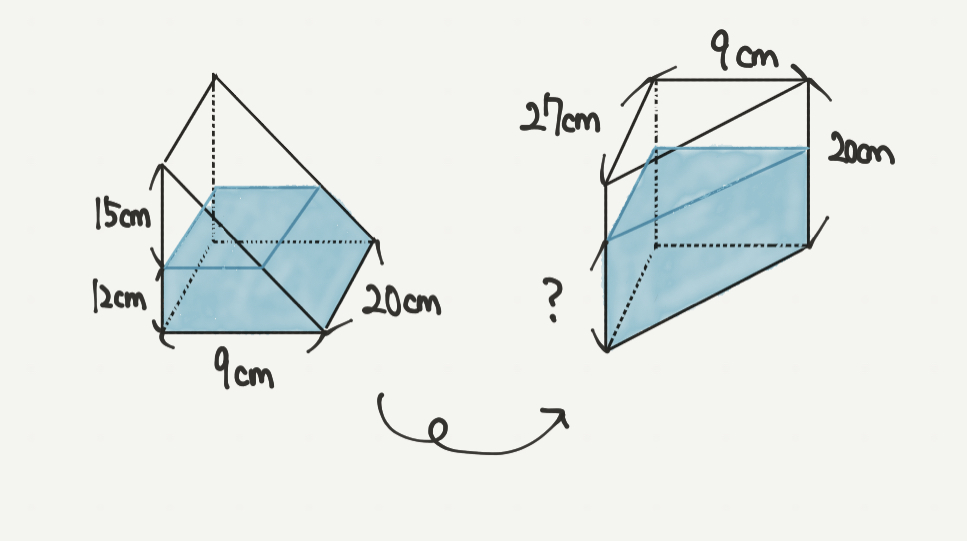
まずは問題文を読んで、求めないといけない部分を理解しましょう。
この問題で言われていることは三角柱を三角形が底面になるように倒す、ということでした。
なので三角柱の中の水の形が変わっていきますね!!
ここでポイントです!
「水の量は形が変わっても同じ」ということを覚えておいてください!
STEP2:水の体積を求めるために必要なことは何か?
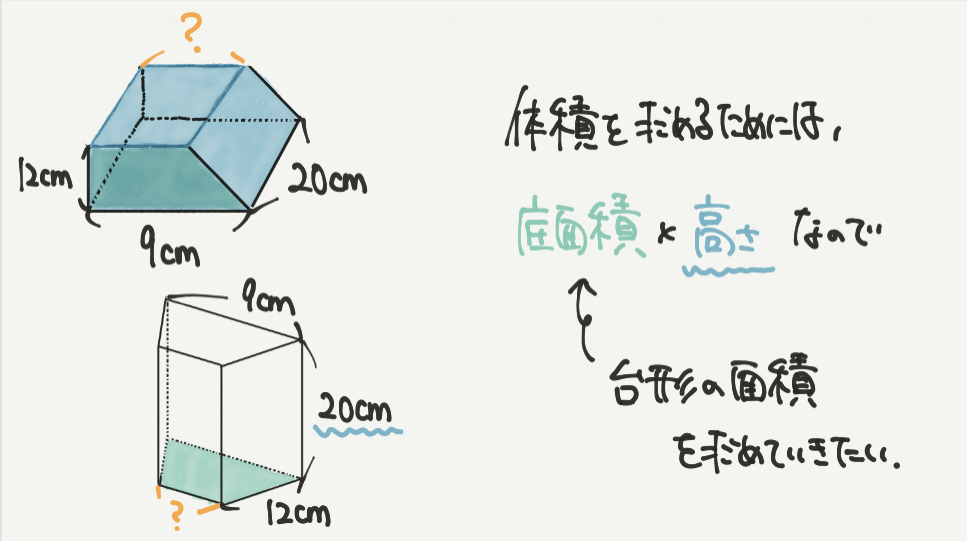
問題文から求めたい内容がわかったら、次は水の体積を求めていきます!
底面を台形にして考えるとわかりやすいので図形の向きを変えて考えましょう。
すると求めたい体積が「底面積×高さ」になるのがわかると思います。
高さは問題文から20cmとわかりますが、底面積の台形の面積がわかりません。
台形の面積を求めるために必要な?の長さがわからないからです。
なので?を求めるためのヒントを探してみましょう。
STEP3:?は相似を使って求めよう
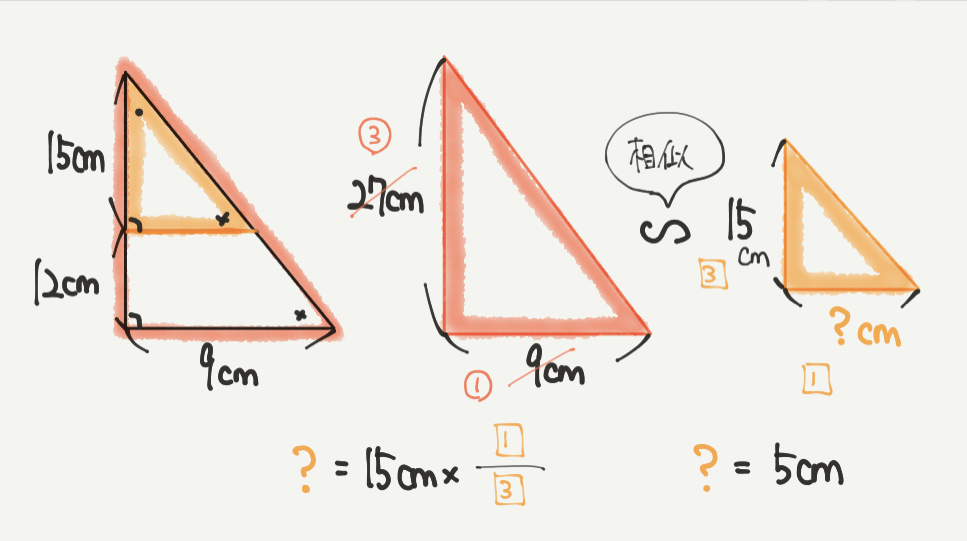
?を求めるために、ここで相似の考え方を使っていきましょう。
注目するのは問題文に書かれている三角柱の側面です!
相似はこの前の問題でも解いたね!!
たしか相似は「形が全く同じで大きさの違う図形」のことだったね!
今回の問題では赤い三角形と黄色の三角形が相似の関係になります。
↑3つの角度が●、✖︎、90°で同じなので相似となります。
意味がわからなかったら一番下に「相似」の復習問題をはっておくので確認してみてくださいね!
赤い三角形はたての長さが27cm、横の長さが9cmなので
たて:横=③:①(3:1)になります。
2つの三角形が相似の関係なので、黄色の三角形のたて:横も3:1になるはずです。
たての長さが15cmなので、横の長さは15cm×1/3で5cmとわかります。
ここまで求めたらあとはラストスパートです。
STEP4:水の体積から答えの高さを求めよう
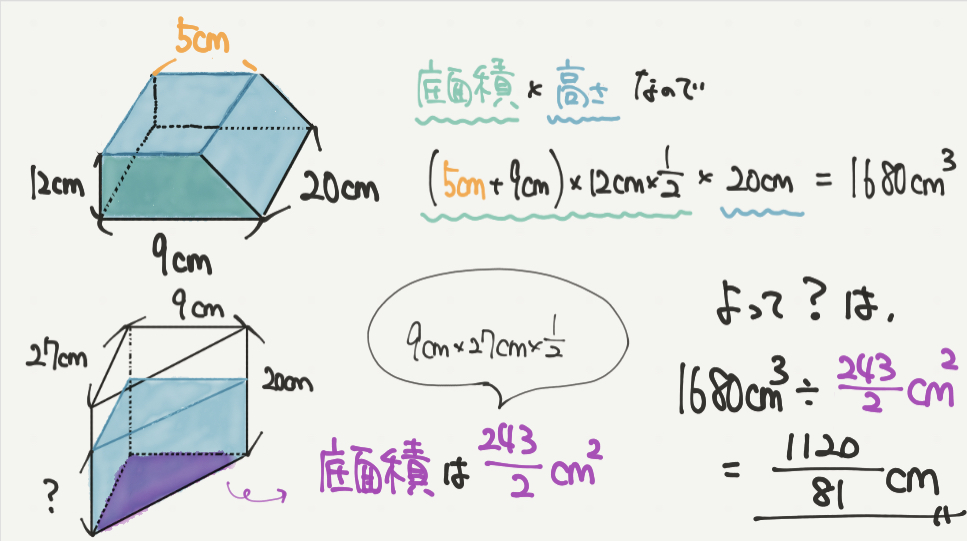
?の長さが5cmとわかってしまえばあとは計算するだけです!!
水の体積はSTEP2で「底面積×高さ」と考えたので、
底面積(台形):(5cm+9cm)×12cm×1/2
↑台形の面積は「(上底+下底)×高さ×1/2」
高さ:20cm
底面積×高さ
=(5cm+9cm)×12cm×1/2×20cm
=1680㎤になります。
今回知りたい三角柱の高さは底面積が、
底面積:9cm×27cm×1/2=243/2㎠
なので求めたい答えは、
1680㎤÷243/2㎠=1120/81cmとなりました!!
 わかみや先生
わかみや先生答えの数字がとてもきたなくなってしまってすいません!!!
水の体積から三角柱の容器の高さを求める問題のまとめ
今回の問題で大事なポイント
- 「同じところを見つける、作る」考え方(STEP1)
・水の量は同じ! - 角柱の体積の求め方(STEP2、4)
・底面積×高さ - 相似の考え方の復習(STEP3)
以上が今回の問題でした!!
いつもやっていたような問題とは違ったタイプの問題でしたがいかがだったでしょうか?
もしわからないところがあれば遠慮なくコメントで質問してくださいね!
今回の問題の正解、不正解を左右したのは解説の図の?の長さを求めることができたかどうか?です。
大事なポイントの中でも特に大切だったのが相似の考え方でした。
相似の図形であれば「辺の長さの比が同じになる」ということを知っていたかどうかで
大きく点数が変わるような問題でした。



相似に関してはまだまだ苦手な受験生が多いと思いますので、
下の復習問題からぜひ挑戦してみてください!
相似に関する復習問題
影の長さから木の高さを求めるには?


相似比と表面積比と面積比を求めるには?