【中学受験算数】苦手の生徒の多い「割合と比」を攻略！問題文から線分図を書いてもともとあった金額を求めてみよう！

はじめに

受験生のみなさん、こんばんは。
今日も中学受験の算数、「割合と比」の問題について勉強していきましょう！

今回の問題では線分図の考え方が出てきます。
みなさん書き方は覚おぼえていますか？

それではさっそく例題からチャレンジしていきましょう！

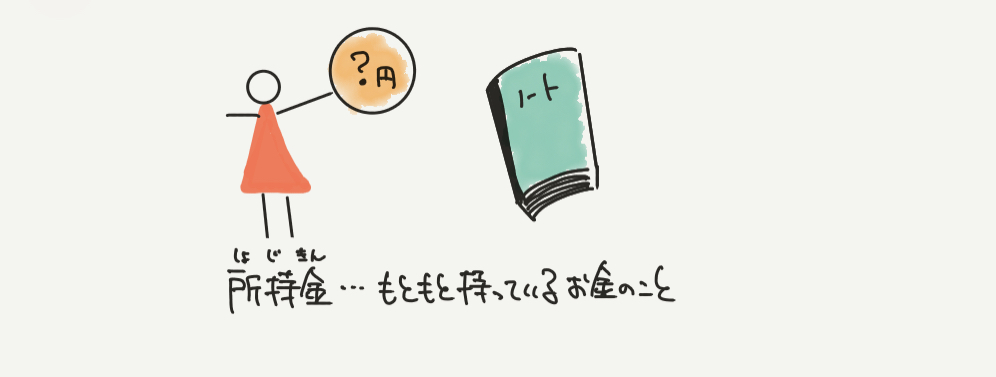
まずは例題から解いてみよう！

赤い小人は所持金しょじきんの1/3のお金でノートを買ったところ、残ったお金が600円になりました。
もともと持っていたお金はいくらですか。

↑所持金しょじきんとは？もともと持っているお金のこと。

解答

900円

解説を見てみよう

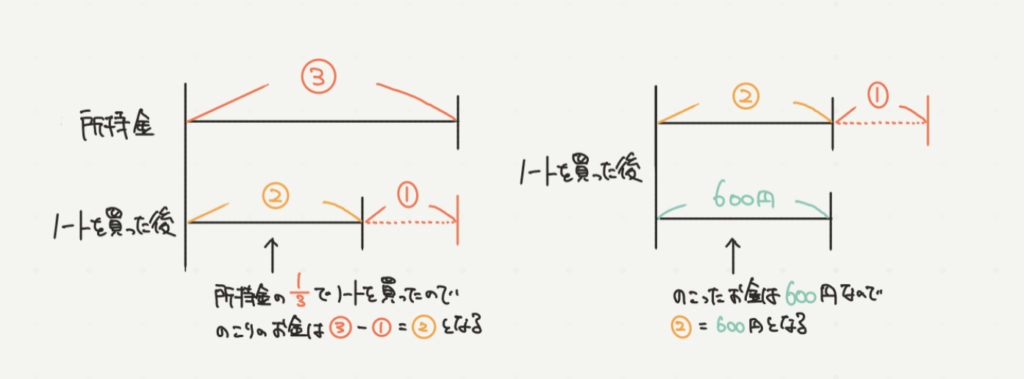
このようなお金の問題は線分図を書くとわかりやすく考えることができます。
まずは左の線分図を見てみましょう。

もとのお金（所持金しょじきん）はわかりませんが、そのお金の1/3のお金でノートを買ったので
所持金しょじきんを③と仮定すれば、ノートのお金は①とわかります。

仮定とは？もし⚪︎⚪︎がXXだったら〜と考える算数の考え方のことです！

すると残のこりのお金は②になりますね！
ここで右の線分図を見てみましょう。

ノートを買って、残のこったお金が600円と言われていますので、②＝600円となります。

ここから、
①＝600円÷2
①＝300円　と求もとめることができます。

よって、所持金（③）は全部で、
300円（①）×3＝900円　になります！

さあ、ここから問題に挑戦ちょうせんしていきましょう！

問題に挑戦ちょうせん！

A君は、所持金しょじきんの1/4よりも200円少ない金額きんがくで教科書を買い、その残りの3/8よりも300円多いお金で辞書じしょを買ったところ、1700円残りました。A君の初めの所持金しょじきんはいくらですか。

解答

この記事を書いている人はこんな人

解説を読んで「 割合と比 」を攻略こうりゃくしよう！

STEP1：線分図を書くまえの準備をしよう

今回の問題は線分図を書くととてもわかりやすいと思います。
なので、STEP1では線分図の書き方のおさらいから始めましょう。

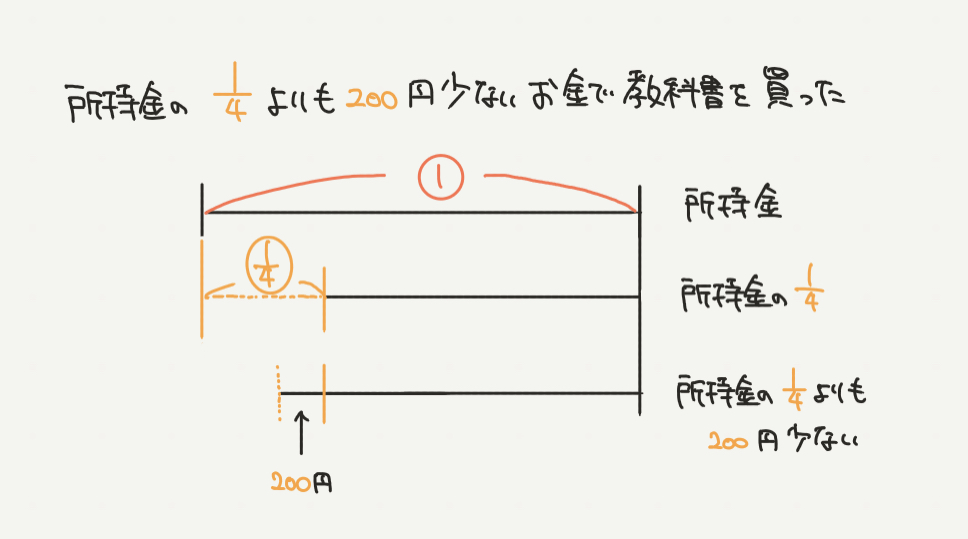
例題でもやったように、所持金しょじきんがいくらか分からないところから書いていきます。
まず、所持金しょじきんの1/4のお金を書いてみると、線分図の真ん中のように書けると思います。

そしてここが少しむずかしいところで、所持金しょじきんの1/4よりも200円少ないお金をどのように線分図に書くのかがポイントになります。
所持金しょじきんの1/4よりも200円少ないお金、なので教科書のお金は所持金しょじきんの1/4よりも200円安いことになります。

つまり、残ったお金は所持金しょじきんの1/4よりも200円多いことがわかりますね！
これをきちんと理解すれば、問題文の内容を全て線分図にすることができます。

STEP2：問題文の内容を図にしよう

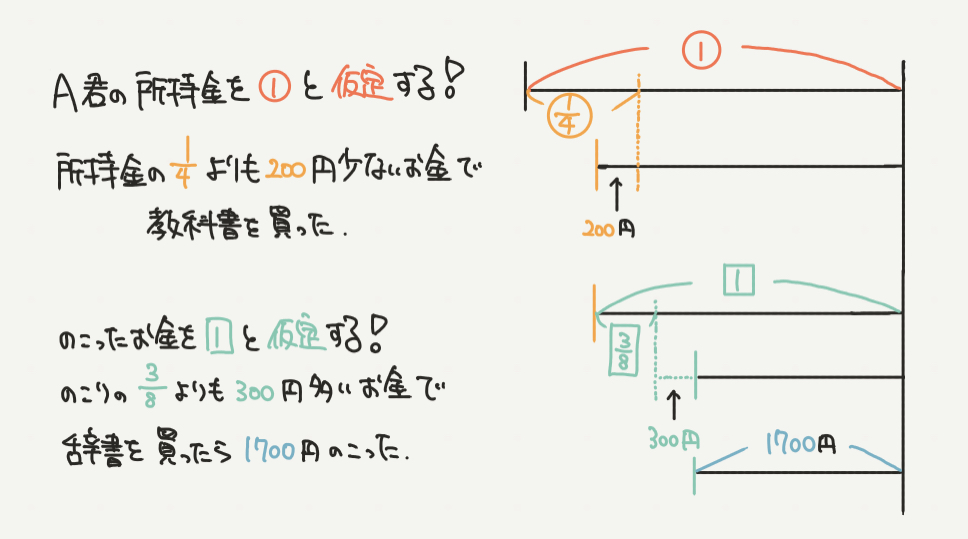
それでは、問題文の内容をきちんと図にしていきましょう。
ここで大事だったことが、もとの所持金を仮定することでした。

今回はA君の所持金を①と仮定し、解いていきましょう。

仮定とは？「もし○○だったら〜」と問題を解きやすくする考え方のこと。
ちなみに、仮定する時の注意点は以下の通りです。

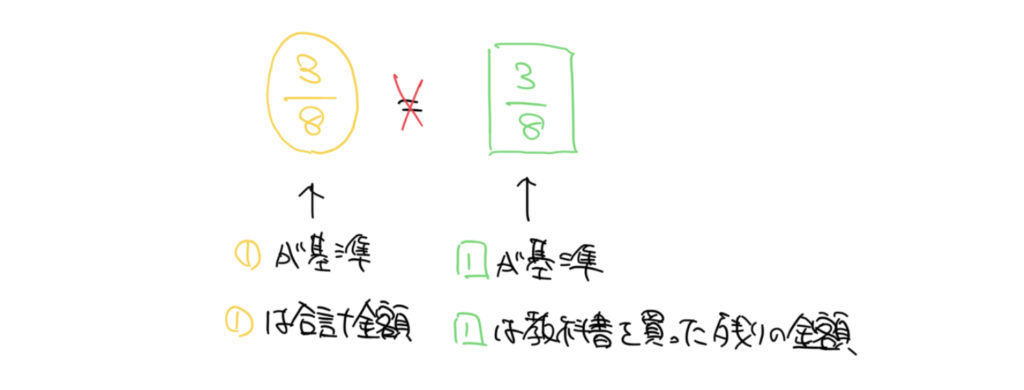
ここで気をつけて欲しいのは緑の部分（残のこりの3/8のところ）を○の3/8にしないことです。
残りのお金（□の１）を基準きじゅんとしたときの3/8なので、○ではなく□の3/8にすることを忘わすれずに考えましょう。

あとは、書いた図から順番に解いていきましょう。

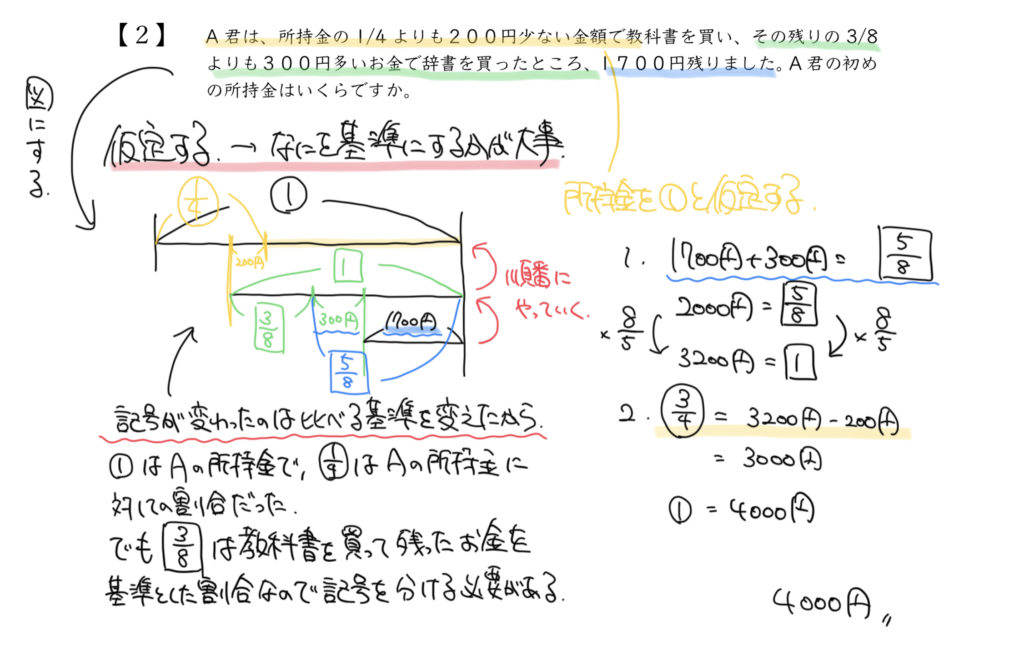
STEP3：1700円から順番に解いていこう

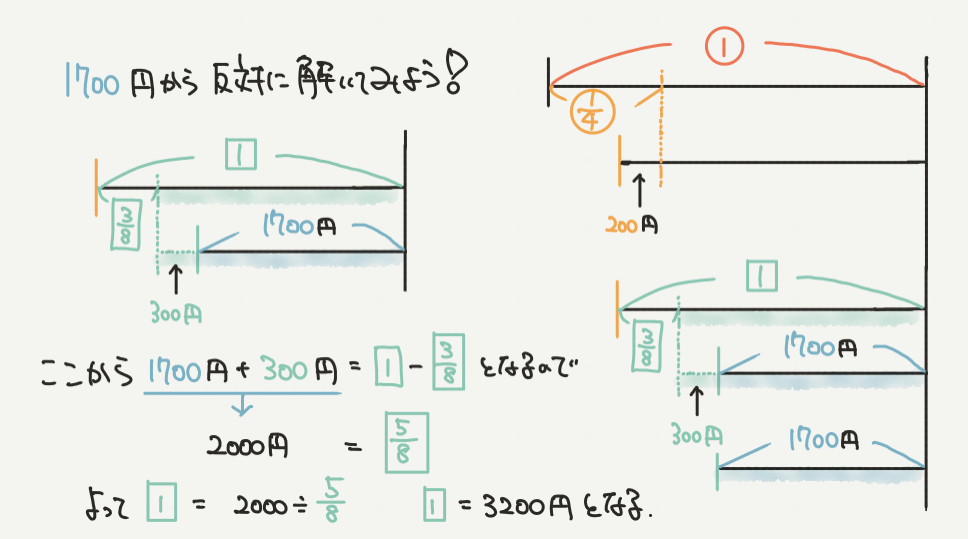
それでは準備じゅんびができたところで、問題を解いていきましょう。
まずは1700円のところからです！

線分図を見てわかるように、1700円＋300円をすると、
□の1-□の3/8＝□の5/8 であることがわかります。

この情報だけ見つけられれば、
2000円＝□の5/8 と求もとめることができますね。

なので□の1は、
2000円÷5/8=2000円×8/5

よって□の1＝3200円となります。
このように順番に記号を一つずつ消して、実際じっさいの数字に直していきましょう。
□の1を実際じっさいの数字の3200円にしていくように、記号を求もとめていきましょう。

STEP4：3200円を代入して①を求もとめる

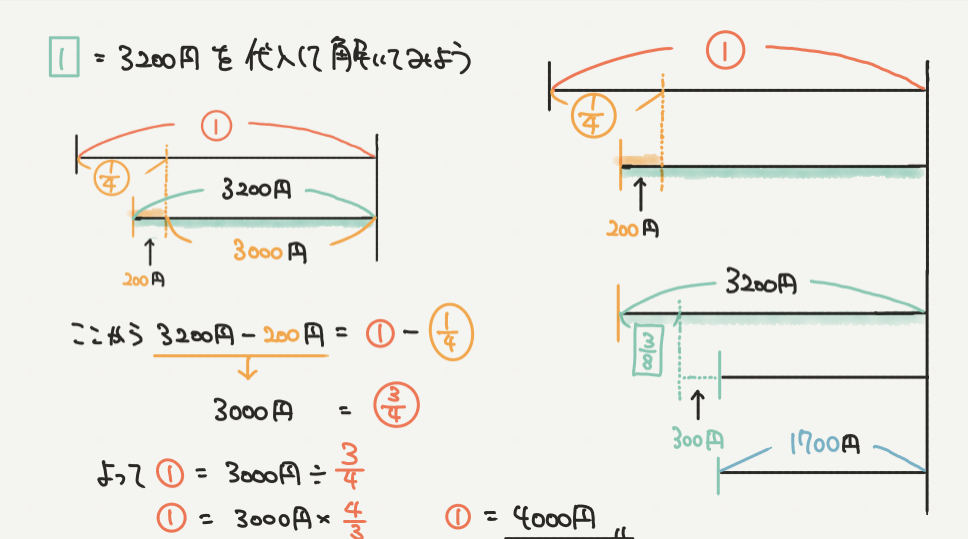
最後もSTEP3と同じように計算していきましょう。
□の1＝3200円 とわかりましたので、その情報を線分図に代入していきます。

ここで上2つの線分図を見てもらうと、答えにたどりつけると思います。
3200円−200円がなにかと同じなのですが、わかりますか？

少し考えてみてください。
はい、そうです！

この3200円−200円＝3000円は、
A君が持っていた所持金しょじきんの○の3/4と同じであることがわかりますね！！

STEP3と同じように、
3000円＝○の3/4 と求もとまります。

なので①は、
3000円÷3/4=3000円×4/3

よって①＝4000円となり、答え（もとの所持金しょじきん）が4000円となります。

残ったお金からもともとあったお金を求める問題のまとめ

今回の問題で大事なポイント

線分図の書き方（STEP1、2）
・なにを基準に考えるのか気をつけよう！
・仮定するときの考え方（STEP2）

以上でこの問題はおしまいです！
おつかれさまでした〜！

「割合と比」の中ではかなりよく出る問題だったと思います。
こういう「もとのお金から少しずつ買い物をして、最後○○円でした！さあもとの所持金しょじきんはいくらでしょう？」てきな問題は受験でもたくさん出てきます。

解説を見ればわかると思いますが、大事なのは計算部分よりもまずはきちんと文章を線分図にすることです。
なので、本当に「割合と比」をカンペキにしたい受験生は、線分図の書き方から復習することをおすすめします！

その他の単元の問題の復習はこちらから！