はじめに
みなさんこんばんは!!
今回解く問題は「時計算」とよばれる問題です。
いつも受験生のみなさんが解いている旅人算とは少し違うので、
しっかり基本をおさえてから問題を解いていきましょう。
まずはヒントから確認です!
時計算の基本!
時計には長い針と短い針がある

時計算の問題では2つの針が出てきます。
長針:時計の長い針のこと
短針:時計の短い針のこと
この長針と短針を使って問題を解きます。
長針と短針の進む速さを求めよう
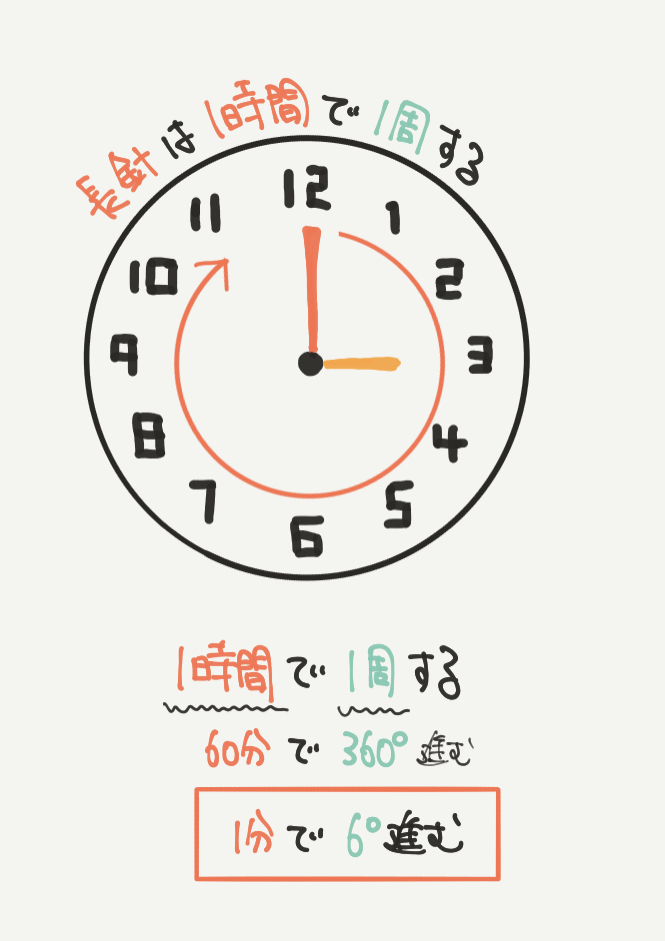
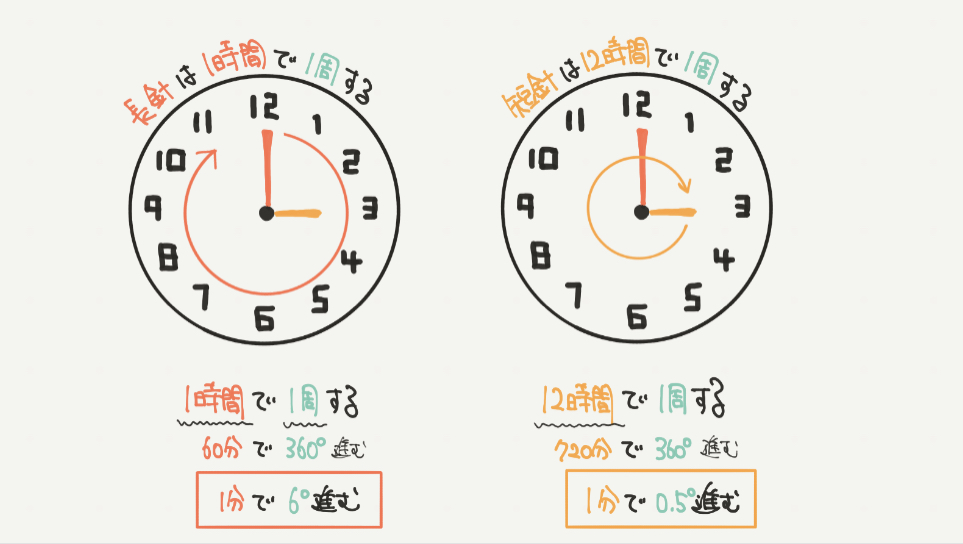
時計の長針は1時間で1周します。
なので1時間で360°進むことがわかります。
よって長針が1分間で進む距離は6°とわかります。
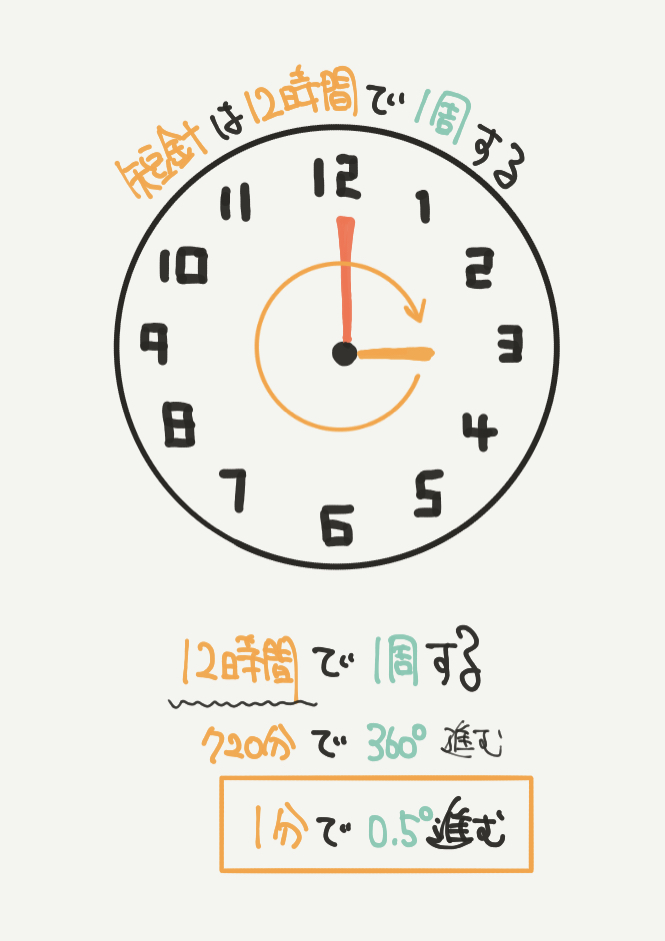
逆に、時計の短針は12時間で1周します。
なので12時間で360°進むことがわかります。
よって短針が1分間で進む距離は0.5°とわかります。
時計の数字の間の角度は30°
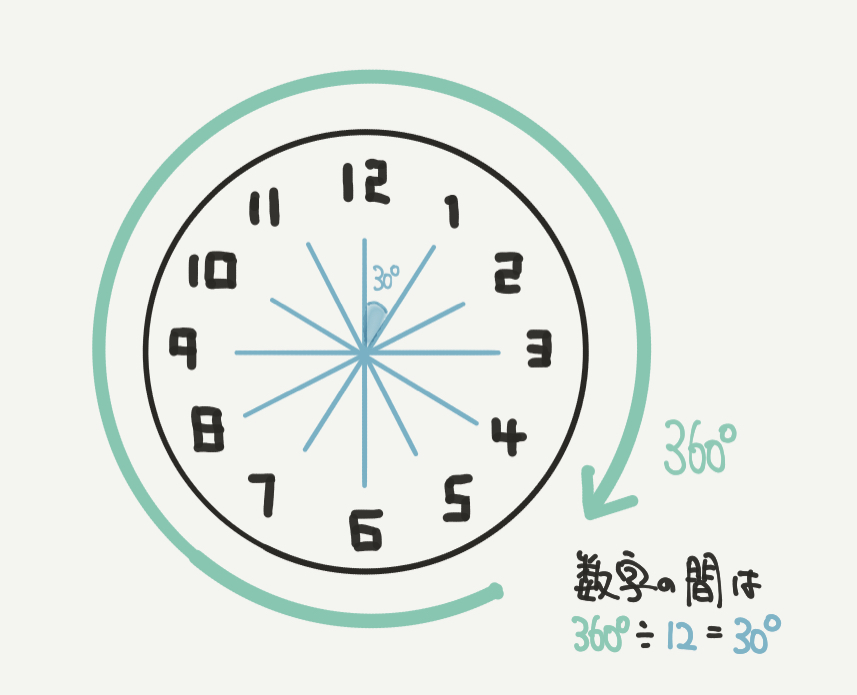
最後に時計の角度について確認しておきましょう。
1周が360°の時計で数字が全部で12個ありますので、数字と数字の間の角度は
360°÷12=30°となります。
ここまでが時計算で絶対に知っておいてもらいたい基本情報でした。
これらの知識を使いながら、さっそく問題に挑戦です。
問題に挑戦!
解答
答えを見るにはここをクリック!
70.5度
この記事を書いている人はこんな人

解説を読んで「 速さ 」を攻略

STEP1:まずは長針と短針の進む速さを確認しよう
最初に時計算のおさらいからです。
まず、長針が1分間で進む距離は6°なので速さは6°/分です。
そして短針が1分間で進む距離は0.5°なので速さは0.5°/分になりましたね。
まずはきちんとここを理解してSTEP2へ行きましょう!
STEP2:7:00の時の角度をまずは求めよう

求めたい角度は7:51のときの角度ですが、まずは7:00のときの角度から考えましょう。
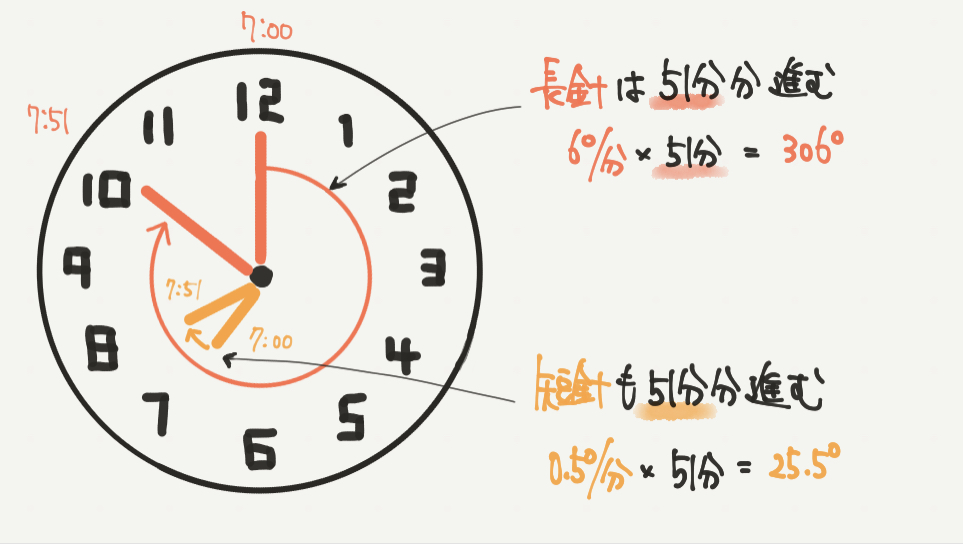
7:00ぴったりのときの角度は
30°×7=210°と分かります。
STEP3:51分で長針と短針がどれくらい進むか考えよう
STEP2で7:00ぴったりのときの角度を求めました。
STEP3ではそこから51分経ったあとの2つの針の角度について計算しましょう。
STEP1で長針と短針の進む速さを求めているので、
長針の進む距離:6°/分×51分=306°
短針の進む距離:0.5°/分×51分=25.5°
と計算することができました。
STEP4:求めたい答えを計算しよう
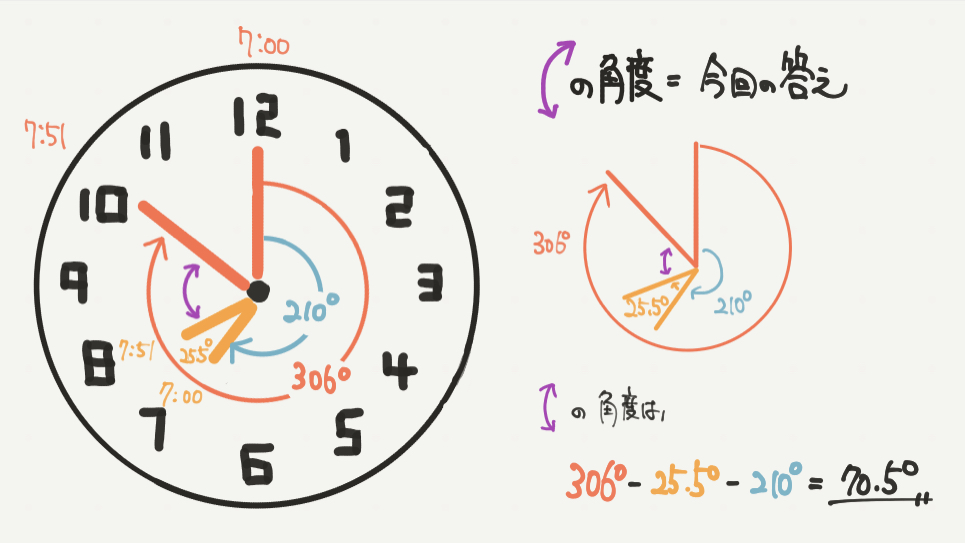
最後に求めたい紫の部分を計算しましょう。
求めたい角度は、306°から25.5°と210°を引いた数になるので
306°–25.5°–210°=70.5°とわかりました。
今回の答えは長針と短針の作る小さい方の角度なので、70.5°が答えになります!
時計の長針と短針の作る角度を求める問題のまとめ
今回の問題で大事なポイント
時計の長針と短針の考え方(STEP1)
・長針の進む速さ
・短針の進む速さ
時計について(数字の間の角度は30°)
以上が時計算の基本問題でした。
おつかれさまでした!!
はじめての時計算の問題だった受験生もいたと思いますが、きちんと理解できましたか?
もしわからないところがあれば下のコメントからいつでも質問してくださいね!!
受験で時計算が出ることはあまりありませんが、
その分受験で出てきたときにきちんと正解できるかが大きな合格ポイントになります。
時計算ではまだまだむずかしい問題もたくさん出てきますので、一緒に次の問題にも挑戦していきましょう!